【10.11校内测试】【优先队列（反悔贪心）】【莫队】【stl的应用？？离线处理+二分】

上次做过类似的题，原来这道还要简单些？？

上次那道题是每天可以同时买进卖出，所以用两个优先队列，一个存买进，一个存卖出（供反悔的队列）。

这道题实际上用一个就够了？？？但是不好理解！！

所以我还是用了俩...

和之前那道题不同的是，如果我选择了反悔，之前第二个队列的队头就完全没有用了，但是我们可以选择重新买它，所以把它重新放到第一个队列。

#include<bits/stdc++.h>
using namespace std;

priority_queue < int, vector < int >, greater < int > > q1, q2;

int n, a[];
long long ans;

int main() {
    freopen("trade.in", "r", stdin);
    freopen("trade.out", "w", stdout);
    scanf("%d", &n);
    for(int i = ; i <= n; i ++)    scanf("%d", &a[i]);
    for(int i = ; i <= n; i ++) {
        int x1, x2, r1 = , r2 = ;
        if(!q1.empty())    {
            x1 = q1.top(); if(a[i] - x1 > )    r1 = a[i] - x1;
        }
        if(!q2.empty())    {
            x2 = q2.top(); if(a[i] - x2 > )    r2 = a[i] - x2;
        }
        if(r1 >= r2 && r1) {
            q1.pop(); q2.push(a[i]); ans += r1;
        } else if(r2 > r1 && r2 ) {
            q2.pop(); q2.push(a[i]); q1.push(x2); ans += r2;
        } else q1.push(a[i]);
    }
    printf("%lld", ans);
    return ;
}

---

这道题乍一看是推公式$O(1)$的数论？？经$yuli$dalao考场上一个多小时的测试发现没有这样的式子....

所以$zc$dalao通过研究打表发现了正解！其实是莫队！

？？？

首先我们也来打一下表....发现了两个递推式：$S_n^m=S_n^{m-1}+C_n^m$和$S_n^m=2S_{n-1}^m-C_{n-1}^m$，我们可以把$[n,m]$看成一个区间来进行离线莫队转移，复杂度$O(n\sqrt{n})$。

#include<bits/stdc++.h>
#define mod 1000000007
#define LL long long
using namespace std;

int blo[];

struct Node {
    int n, m, id;
} qus[];
bool cmp(Node a, Node b) { if(blo[a.m] == blo[b.m]) return a.n < b.n; return a.m < b.m; }

LL fac[], inv[];
LL C(int n, int m) {
    if(m > n)    return ;
    return fac[n] * inv[m] % mod * inv[n - m] % mod;
}

LL mpow(LL a, LL b) {
    LL ans = ;
    for(; b; b >>= , a = a * a % mod)
        if(b & )    ans = ans * a % mod;
    return ans;
}

void init() {
    fac[] = ; inv[] = , inv[] = ;
    for(int i = ; i <= ; i ++)
        fac[i] = fac[i - ] * i % mod;
    for(int i = ; i <= ; i ++)
        inv[i] = mpow(fac[i], mod - );
    for(int i = ; i <= ; i ++)    blo[i] = i/ + ;
}

int Ans[];
int main() {
    freopen("sum.in", "r", stdin);
    freopen("sum.out", "w", stdout);
    int id;
    scanf("%d", &id);
    init();
    int T;
    scanf("%d", &T);
    for(int i = ; i <= T; i ++)
        scanf("%d%d", &qus[i].n, &qus[i].m), qus[i].id = i;
    sort(qus + , qus +  + T, cmp);

    int n = qus[].n, m = qus[].m; LL ans = ;
    for(int i = ; i <= m; i ++)    ans = (ans + C(n, i)) % mod;
    Ans[qus[].id] = ans;
    for(int i = ; i <= T; i ++) {
        while(qus[i].m < m) {
            ans = (ans - C(n, m) + mod) % mod;
            m --;
        }
        while(qus[i].n > n) {
            ans = (2LL * ans % mod - C(n, m) + mod) % mod;
            n ++;
        }
        while(qus[i].m > m) {
            m ++;
            ans = (ans + C(n, m)) % mod;
        }
        while(qus[i].n < n) {
            n --;
            ans = 1LL * (ans + C(n, m)) * inv[] % mod;
        }
        Ans[qus[i].id] = ans;
    }
    for(int i = ; i <= T; i ++)    printf("%d\n", Ans[i]);
    return ;
}

感觉这种题就算让我再做一次，也写不出来...重载什么的简直太难记了aaa！！

对于第一个询问，直接分别处理每行和每列就行了，每行就直接加，每列用差分处理。

如何查找联通块数量？

分别处理两种情况：

1）与下边相交对于上面的矩形，查找它下一排最后一个与它相交的矩形，向前枚举直到不相交，把相交的矩形连边。

2）与右边相交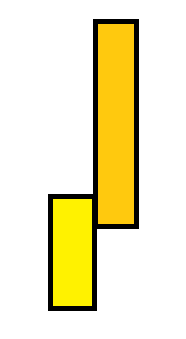对于左边的矩形，查找它右边与它相交的所有矩形，连边。

以上操作用二分实现。注意的是，因为我们建边是在每排的基础上（因为查询的是排），所以第一种应该建在下面那排，第二种应该建在两个矩形上边界的排取max。（查询前缀时才能保证合法）

stl（vector简直tql！QAQ）

#include<bits/stdc++.h>
#define LL long long
using namespace std;

int ans2[];
LL ans1[], sum2[], sum1[];

struct Data {
    int lx, ly, rx, ry;
    Data(int lx = , int ly = , int rx = , int ry = ) :
        lx(lx), ly(ly), rx(rx), ry(ry) { }
} A[];

struct Node {
    int id, l, r;
    Node(int id = , int l = , int r = ) :
        id(id), l(l), r(r) { }
};

vector < Node > row[], col[];
bool operator < (const Node &a, const Node &b) {
    return a.l < b.l || (a.l == b.l && a.r < b.r);
}

vector < pair < int , int > > G[];

int root[], edge, num;
int find(int x) {
    if(root[x] != x)    root[x] = find(root[x]);
    return root[x];
}

void merge(int x, int y) {
    x = find(x); y = find(y);
    if(x != y)    root[x] = y, ++ edge;
}

int main() {
    freopen("building.in", "r", stdin);
    freopen("building.out", "w", stdout);
    int opt;
    scanf("%d", &opt);
    int n, m, k, p;
    scanf("%d%d%d%d", &n, &m, &k, &p);
    for(int i = ; i <= k; i ++) {
        int lx, ly, rx, ry;
        scanf("%d%d%d%d", &lx, &ly, &rx, &ry);
        A[i] = Data(lx, ly, rx, ry);
        row[lx].push_back(Node(i, ly, ry));
        col[ly].push_back(Node(i, lx, rx));
        if(lx == rx)    sum1[lx] += (ry - ly + );
        else sum2[lx] ++, sum2[rx + ] --;
    }
    for(int i = ; i <= n; i ++)    sort(row[i].begin(), row[i].end());
    for(int i = ; i <= m; i ++)    sort(col[i].begin(), col[i].end());
    for(int i = ; i <= k; i ++) {
        int down = A[i].rx + ;
        if(down <= n && row[down].size()) {
            int p = upper_bound(row[down].begin(), row[down].end(), Node(, A[i].ry, m + )) - row[down].begin() - ;
            for(; p >=  && row[down][p].r >= A[i].ly; p --)
                G[down].push_back(make_pair(i, row[down][p].id));
        }
        int right = A[i].ry + ;
        if(right <= m && col[right].size()) {
            if(right < )    return ;
            int p = upper_bound(col[right].begin(), col[right].end(), Node(, A[i].rx, n + )) - col[right].begin() - ;
            for(; p >=  && col[right][p].r >= A[i].lx; p --)
                G[max(A[i].lx, A[col[right][p].id].lx)].push_back(make_pair(i, col[right][p].id));
        }
    }
    for(int i = ; i <= n; i ++)    sum2[i] += sum2[i-];
    for(int i = ; i <= n; i ++) {
        sum2[i] += sum2[i-];
        sum1[i] += sum1[i-];
        ans1[i] = sum1[i] + sum2[i];
    }
    for(int i = ; i <= k; i ++)    root[i] = i;
    for(int i = ; i <= n; i ++) {
        num += row[i].size();
        for(int j = ; j < G[i].size(); j ++)    merge(G[i][j].first, G[i][j].second);
        ans2[i] = num - edge;
    }
    while(p --) {
        int u, v;
        scanf("%d%d", &u, &v);
        if(u)    printf("%d\n", ans2[v]);
        else    printf("%lld\n", ans1[v]);
    }
    return ;
}