单纯形法MATALAB实现
参考单纯形法的步骤,MATALAB中的实现如下(求极小值):
注:对于极大值的求解,只需要对目标函数添加负号,求解出来的\(X\),再带入原目标函数即可。
function [ X, z ] = simplex( A, b, C )
% 单纯形法的实现
% X: 目标函数的最优解
% z: 目标函数的极小值
% A: 约束函数的系数矩阵
% b: 约束函数的常数列向量
% C: 目标函数的系数向量
[m, n] = size(A);
BIndex = n - m + 1 : n; % 基向量下标集合
NIndex = 1 : n - m; % 非基向量下标集合
flag = 1;
if (n < m)
disp('系数矩阵不符合要求!')
else
while flag
B = A(:, BIndex); % 基矩阵
N = A(:, NIndex); % 非基矩阵
cb = C(BIndex); % 基矩阵对应的目标值cb
cn = C(NIndex); % 非基矩阵对应的目标值cn
xb = B \ b;
X = zeros(1, n); X(BIndex) = xb;
z = cb * xb; % 目标函数值
sigma = cn - cb / B * N; % 判别数
[v, k] = min(sigma); % k是进基向量下标
if v > 1e-5
flag = 0;
disp('已找到最优解:')
else
[~, l] = min((B \ b) ./ (B \ A(:, k))); l = BIndex(l); % l是出基向量下标
BIndex(BIndex == l) = k; % 更新基向量下标集合
NIndex(NIndex == k) = l; % 更新非基向量下标
end
end
end
end
对于单纯形法中的例子,求解如下:
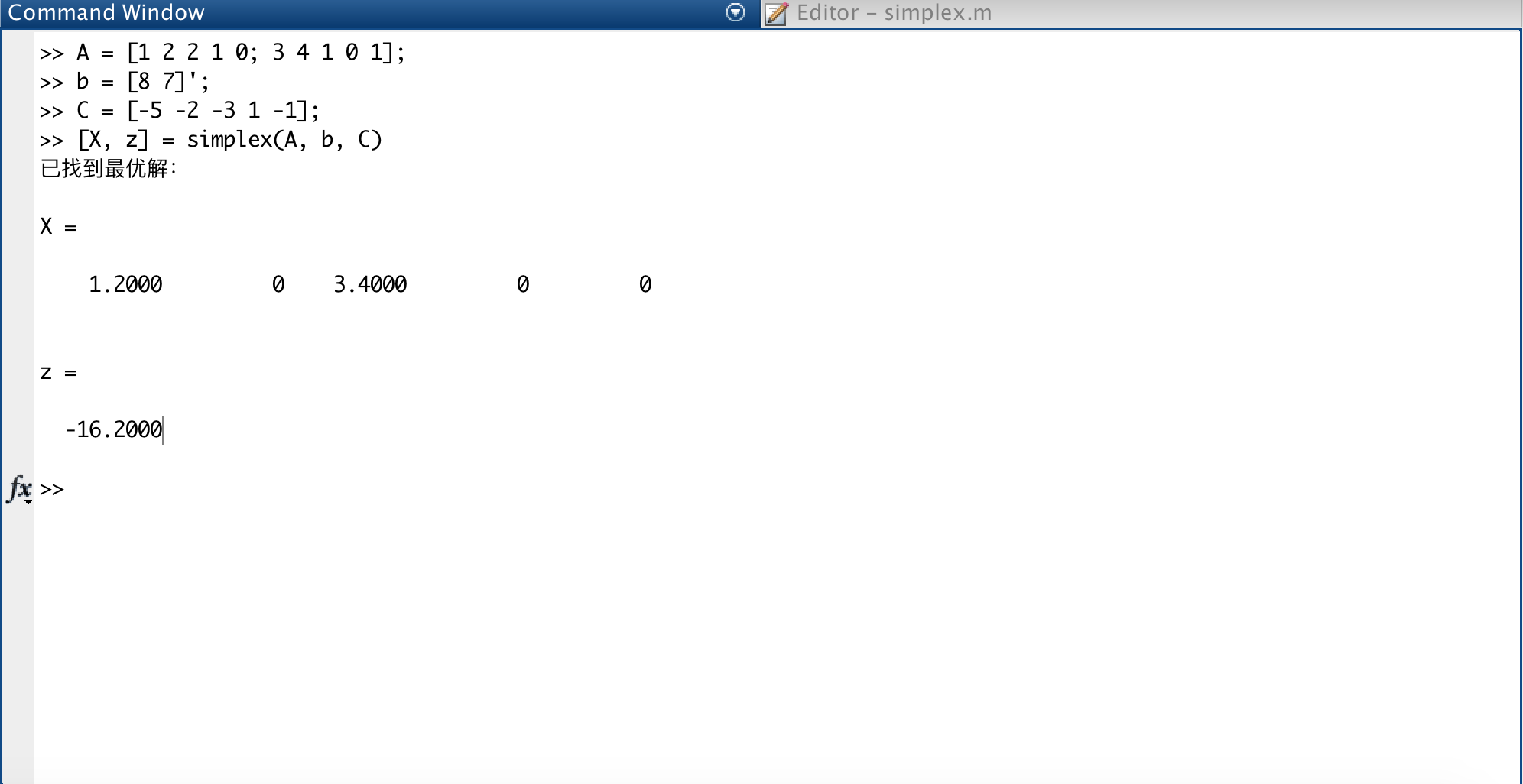
单纯形法MATALAB实现的更多相关文章
- BZOJ 1061: [Noi2008]志愿者招募 [单纯形法]【学习笔记】
1061: [Noi2008]志愿者招募 Time Limit: 20 Sec Memory Limit: 162 MBSubmit: 3975 Solved: 2421[Submit][Stat ...
- Ubuntu16.04 安装MATALAB R2015b教程
1.安装 将镜像文件内文件解压出来,添加执行权限,否则执行 ./install指令会出错 chmod -R 777 MATALAB 执行如下指令 ./install 2.填入补丁内的密匙 在Matla ...
- BZOJ 1061: [Noi2008]志愿者招募 [单纯形法]
传送门 题意: 长为$n$的序列,第$i$位至少$b_i$,$m$种区间使$[l_i,r_i]+1$代价为$a_i$ 求满足的最小花费 复习单纯形法重做一遍 原始问题$m$个变量$n$个约束,$a_{ ...
- 智能优化 之 下山单纯形法 C++
单纯形法简介在其他网站上都可以查到,我就不多说了 我们主要说方法 它主要解决的是局部最优解的问题 利用多边形进行求解的,若有n个变量,则利用n+1边形 我们这里以两个变量为例,求解第三维度的最优解 例 ...
- BZOJ 1061: [Noi2008]志愿者招募 [单纯形法]【学习笔记看另一篇吧】
1061: [Noi2008]志愿者招募 Time Limit: 20 Sec Memory Limit: 162 MBSubmit: 3975 Solved: 2421[Submit][Stat ...
- 能用的单纯形法python代码
网上找了一些代码,发现有一些是不能用的,出现错误说集合为空 1.网上出现了好多次,但是不能用的,只能部分模型能用,比如例子中所示 原链接:https://www.jianshu.com/p/b233c ...
- POJ1275 Cashier Employment[差分约束系统 || 单纯形法]
Cashier Employment Time Limit: 1000MS Memory Limit: 10000K Total Submissions: 7997 Accepted: 305 ...
- BZOJ 3112: [Zjoi2013]防守战线 [单纯形法]
题目描述 战线可以看作一个长度为n 的序列,现在需要在这个序列上建塔来防守敌兵,在序列第i 号位置上建一座塔有Ci 的花费,且一个位置可以建任意多的塔,费用累加计算.有m 个区间[L1, R1], [ ...
- Matalab IFS分形算法
IFS 算法代码 function IFS_draw(M,p) N=; :length(p); eval(['a',num2str(k),'=reshape(M(',num2str(k),',:),2 ...
随机推荐
- 自定义控件(视图)2期笔记14:自定义视图之View事件分发 dispatchTouchEvent,onTouch,onTouchEvent,onClick逻辑顺序过程
1. 这里我们先从案例角度说明dispatchTouchEvent,onTouch,onTouchEvent,onClick逻辑顺序过程: (1)首先我们重写一个MyButton 继承自 Button ...
- OpenCV2马拉松第2圈——读写图片
收入囊中 用imread读取图片 用nameWindow和imshow展示图片 cvtColor彩色图像灰度化 imwrite写图像 Luv色彩空间转换 初识API 图像读取接口 image = im ...
- Node.js框架之Egg.js
Node.js是我前段时间接触的一个JavaScript的服务端语言,感觉还是挺有意思的. 也许有人说,你学这么多,学的过来吗?或者说学的太多,专而不精,有必要这样吗? 其实,我个人认为,自从我进入I ...
- 使用JS与jQuery实现文字逐渐出现特效
该需求出现原因:想要实现一个在一开始加载页面时就出现一行文字逐渐出现的效果,且需要实现的是一种逐渐的过渡出现效果为不是一种生硬的突然间歇性出现.于是便开始尝试利用最近正在学习的jQuery技术和JS实 ...
- MAC & Xcode 快捷键的使用
"磨刀不费砍材工",在熟悉了MAC 和 Xcode 快捷键后一定可以帮助我们更快捷方便的开发程序 MAC 快捷键: command + Q = 退出应用程序 command + c ...
- 七、Delphi10.3读取JSON数组
一.Delphi读取JSON数组是非常方便的,首先我们网上找一段JSON数据 { "error": 0, "status": "success&quo ...
- GHOST自动恢复说明
制作一个自己DIY的PE系统,然后自动安装系统使用如下步骤... 1: 首先要解包PE ISO文件,在解压ISO中的WIM文件.使用工具是7Zip,可以直接解压 2: 其次在放入替换的exe文件. ...
- SuperObject Delphi 的 JSON 属性乱序 - 操作类改造 - 关于属性顺序的问题
Delphi 的 ISuperObject 属性顺序为随机.但是很多时候,是需要按加入顺序进行读取.我也看了网上很多人有类似需求.也有人问过原作者,作者答复为:JSON协议规定为无序.看了我真是无语. ...
- rails使用Kindeditor网页编辑器
在gemfile中加入(后面版本别丢) gem 'rails_kindeditor', '~> 0.5.0' $ bundle 创建配置文件,并且引入js rails g rails_kinde ...
- 2017-2018-1 20155313 《信息安全系统设计基础》 Myod
2017-2018-1 20155313 <信息安全系统设计基础> Myod Myod要求 1.复习c文件处理内容 2.编写myod.c 用myod XXX实现Linux下od -tx - ...
