[HNOI2002]营业额统计（splay基础）

嘟嘟嘟




这几天开始搞平衡树了，\(splay\)理解起来感觉还行，然而代码看了半天才勉强看懂。

我这篇博客应该不算什么入门讲解，因为我觉得我讲不明白，所以只能算自己的学习笔记吧。




这道题就是有\(n\)个数，定义\(f_i = min{|a_i - a_j|}, 1 \leqslant j < i\)，其中\(f_1 = a_1\)。然后求\(\sum{f_i}\)。

解法就是每添加一个数，查找这个数的前驱和后继，然后取更小的作为\(f_i\)。因此这需要平衡树维护。




那就先简单说一下\(splay\)。

众所周知，普通的\(bst\)最坏情况下会退化成一条链，导致操作变成了\(O(n)\)。因此就有很多大佬发明了各种平衡树来保持复杂度，\(splay\)就算一种。

\(splay\)通过旋转维护树的形态，使树看起来尽量平衡，从而保持每一个操作都是\(O(\log{n})\)。

每添加一个节点\(x\)，都会把\(x\)转到根，从而避免树退化成链。

具体的旋转分为右旋\((zig)\)和左旋\((zag)\)，然后不同的情况这两种旋转的顺序也会不一样。

第一种：



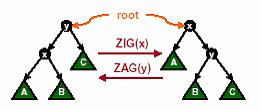
（感谢\(gg\)的图）

这个图已经表达的很明白了，如果\(x\)的父亲就是根节点的话，旋转一次即可，根据方向用\(zig\)或者\(zag\)。

第二种：



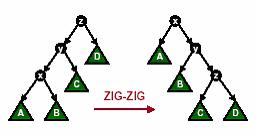
更多的是\(x\)的父亲不是根节点，这种情况是\(x\)和\(y\)在\(y\)的父亲\(z\)的同侧。这个时候要旋转两步，先把\(y\)旋转到\(z\)上，再把\(x\)旋转到\(y\)上。

第三种：



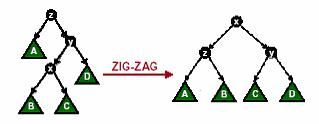
这个是\(y\)在\(z\)的一侧，而\(x\)在\(y\)的另一侧。这个时候应该先把\(x\)旋转到\(y\)上，在把\(x\)旋转到\(z\)上。至于为什么这个顺序，我也不是很清楚。但是反正这样转完后看起来确实很平衡。




理解起来好像还行。但是代码就不太友善了。我学的是把\(zig\)和\(zag\)放一块的写法，代码精简但比较难懂，估计还得消化一阵子吧。

我觉得理解起来的关键就是不要想是左还是右，而是用“这个儿子”和“另一个儿子”去表示。

void pushup(int now)
{
  t[now].siz = t[t[now].ch[0]].siz + t[t[now].ch[1]].siz + t[now].cnt;
}
bool get(int x)
{
  return t[t[x].fa].ch[1] == x;
}
void rotate(int x)
{
  int y = t[x].fa, z = t[y].fa, k = get(x); //k:x是y的哪一个儿子
  t[z].ch[t[z].ch[1] == y] = x; t[x].fa = z; //z的儿子从y换成x,就是
  t[y].ch[k] = t[x].ch[k ^ 1]; t[t[y].ch[k]].fa = y;
  //如果x是y的右儿子,那么y的右儿子现在变成了x的左儿子
  t[x].ch[k ^ 1] = y; t[y].fa = x;
  //然后x的右儿子现在是y
  pushup(x); pushup(y);
}
void splay(int x, int s) //把x旋转到s,这题s传的都是0
{
  //注意：树的根其实是0号节点的孩子，之所以传0,是为了写的方便
  while(t[x].fa != s)
    {
      int y = t[x].fa, z = t[y].fa;
      if(z != s)  //这表示的是x还得再转两次,所以如果s就是根的话,转一次的情况就不直到怎么判了
	{
	  //x, y同向先转y,否则先转x
	  //额外转一次
	  if((t[y].ch[0] == x) != (t[z].ch[0] == y)) rotate(x);
	  else rotate(y);
	}
      rotate(x); //在转一次
    }
  if(!s) root = x; //只有x要转到根的时候才更新根
}

\(splay\)函数我得再说一下。就是他不仅可以旋转到根，到任意一个祖先节点都行，但是这道题只用旋转到跟就行了。




然后是几个基本操作：

1.插入权值为\(x\)的元素

如果当前节点大于\(x\)，就向左递归，否则向右，如果已经有了，就停止。

所以每一个节点有一个\(cnt\)，记录权值为\(val\)的数有多少个。

如果没有，就要新建节点，具体看代码好了。

bool insert(int x)   //非递归版
{
  int now = root, f = 0;
  bool flg = 0;  //flg是因为这道题需要,跟splay没有关系
  while(now && t[now].val != x) f = now, now = t[now].ch[x > t[now].val];
  if(now) t[now].cnt++, flg = 1;   //这个数已经有了
  else
    {
      now = ++ncnt;
      if(f) t[f].ch[x > t[f].val] = now; //来个判断是为了整棵树还没有节点的情况
      t[now].fa = f;
      t[now].ch[0] = t[now].ch[1] = 0;
      t[now].val = x;
      t[now].siz = t[now].cnt = 1;
    }
  splay(now, 0);
  return flg;
}

2.查找权值为\(x\)的元素

这个很简单，

代码里找到后顺便旋了上去，这个是为了找前驱后继用的。

void find(int x)
{
  int now = root;
  if(!now) return;
  while(t[now].ch[x > t[now].val] && t[now].val != x) now = t[now].ch[x > t[now].val];
  splay(now, 0);
}

3.找\(x\)的前驱，后继

我的做法是先找到\(x\)，然后把他旋到根（此题保证\(x\)存在），这样的话找前驱就是走一步左儿子，再右儿子一直走到底。

后继同理：走一步右儿子，然后左儿子走到底。

int pre(int x)
{
  find(x);  //找到并把x旋到根
  int now = t[root].ch[0];
  while(t[now].ch[1]) now = t[now].ch[1];
  return t[now].val;
}
int nxt(int x)
{
  find(x);
  int now = t[root].ch[1];
  while(t[now].ch[0]) now = t[now].ch[0];
  return t[now].val;
}

这道题只用到这几个操作，所以我就说这么多啦。
最后发一下完整代码
```c++
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
#define enter puts("")
#define space putchar(' ')
#define Mem(a, x) memset(a, x, sizeof(a))
#define rg register
typedef long long ll;
typedef double db;
const int INF = 0x3f3f3f3f;
const db eps = 1e-8;
const int maxn = 1e5 + 5;
inline ll read()
{
ll ans = 0;
char ch = getchar(), last = ' ';
while(!isdigit(ch)) last = ch, ch = getchar();
while(isdigit(ch)) ans = (ans = 10) write(x / 10);
putchar(x % 10 + '0');
}

int n, ans = 0;

struct Tree

{

int ch[2], fa;

int siz, cnt, val;

}t[maxn << 1];

int root = 0, ncnt = 0;

void pushup(int now)

{

t[now].siz = t[t[now].ch[0]].siz + t[t[now].ch[1]].siz + t[now].cnt;

}

bool get(int x)

{

return t[t[x].fa].ch[1] == x;

}

void rotate(int x)

{

int y = t[x].fa, z = t[y].fa, k = get(x);

t[z].ch[t[z].ch[1] == y] = x; t[x].fa = z;

t[y].ch[k] = t[x].ch[k ^ 1]; t[t[y].ch[k]].fa = y;

t[x].ch[k ^ 1] = y; t[y].fa = x;

pushup(x); pushup(y);

}

void splay(int x, int s)

{

while(t[x].fa != s)

{

int y = t[x].fa, z = t[y].fa;

if(z != s)

{

if((t[y].ch[0] == x) != (t[z].ch[0] == y)) rotate(x);

else rotate(y);

}

rotate(x);

}

if(!s) root = x;

}

bool insert(int x)

{

int now = root, f = 0;

bool flg = 0;

while(now && t[now].val != x) f = now, now = t[now].ch[x > t[now].val];

if(now) t[now].cnt++, flg = 1;

else

{

now = ++ncnt;

if(f) t[f].ch[x > t[f].val] = now;

t[now].fa = f;

t[now].ch[0] = t[now].ch[1] = 0;

t[now].val = x;

t[now].siz = t[now].cnt = 1;

}

splay(now, 0);

return flg;

}

void find(int x)

{

int now = root;

if(!now) return;

while(t[now].ch[x > t[now].val] && t[now].val != x) now = t[now].ch[x > t[now].val];

splay(now, 0);

}

int pre(int x)

{

find(x);

int now = t[root].ch[0];

while(t[now].ch[1]) now = t[now].ch[1];

return t[now].val;

}

int nxt(int x)

{

find(x);

int now = t[root].ch[1];

while(t[now].ch[0]) now = t[now].ch[0];

return t[now].val;

}

int main()

{

n = read();

insert(INF); insert(-INF);

int x = read(); ans += x; insert(x);

for(int i = 2; i <= n; ++i)

{

int x = read();

if(insert(x)) continue;

int a = pre(x), b = nxt(x);

ans += min(x - a, b - x);

}

write(ans), enter;

return 0;

}