[MCM] K-mean聚类与DBSCAN聚类 Python

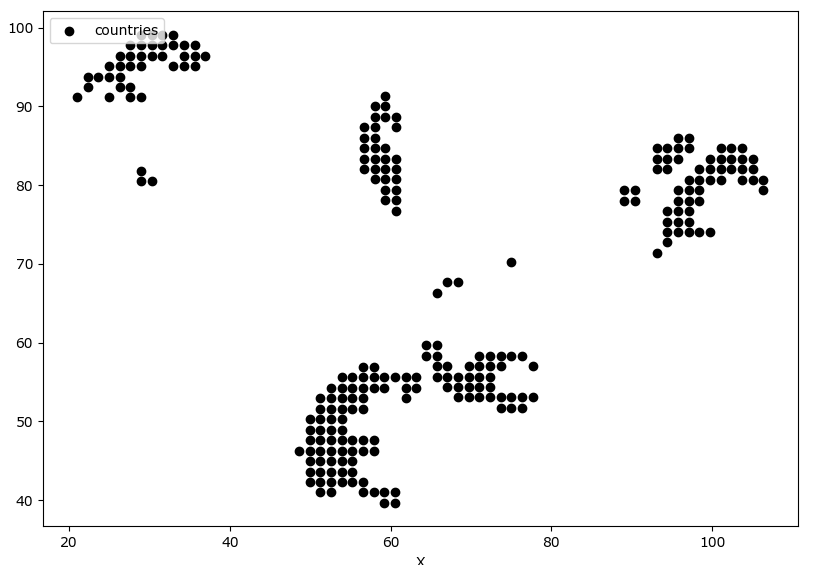
import matplotlib.pyplot as plt

X=[56.70466067,56.70466067,56.70466067,56.70466067,56.70466067,58.03256629,58.03256629,58.03256629,58.03256629,58.03256629,58.03256629,58.03256629,58.03256629,59.3604719,59.3604719,59.3604719,59.3604719,59.3604719,59.3604719,59.3604719,59.3604719,59.3604719,60.68837752,60.68837752,60.68837752,60.68837752,60.68837752,60.68837752,60.68837752,60.68837752,21.00466067,22.33256629,22.33256629,23.6604719,24.98837752,24.98837752,24.98837752,26.31628314,26.31628314,26.31628314,26.31628314,27.64418876,27.64418876,27.64418876,27.64418876,27.64418876,28.97209438,28.97209438,28.97209438,28.97209438,28.97209438,28.97209438,28.97209438,30.3,30.3,30.3,30.3,31.62790562,31.62790562,31.62790562,32.95581124,32.95581124,32.95581124,34.28371686,34.28371686,34.28371686,35.61162248,35.61162248,35.61162248,36.9395281,89.10466067,89.10466067,90.43256629,90.43256629,93.08837752,93.08837752,93.08837752,93.08837752,94.41628314,94.41628314,94.41628314,94.41628314,94.41628314,94.41628314,94.41628314,95.74418876,95.74418876,95.74418876,95.74418876,95.74418876,95.74418876,95.74418876,95.74418876,97.07209438,97.07209438,97.07209438,97.07209438,97.07209438,97.07209438,97.07209438,97.07209438,98.4,98.4,98.4,98.4,98.4,99.72790562,99.72790562,99.72790562,99.72790562,101.0558112,101.0558112,101.0558112,101.0558112,102.3837169,102.3837169,102.3837169,103.7116225,103.7116225,103.7116225,103.7116225,105.0395281,105.0395281,105.0395281,106.3674337,106.3674337,64.40466067,64.40466067,65.73256629,65.73256629,65.73256629,65.73256629,65.73256629,67.0604719,67.0604719,67.0604719,67.0604719,68.38837752,68.38837752,68.38837752,68.38837752,69.71628314,69.71628314,69.71628314,69.71628314,71.04418876,71.04418876,71.04418876,71.04418876,71.04418876,72.37209438,72.37209438,72.37209438,72.37209438,72.37209438,73.7,73.7,73.7,73.7,75.02790562,75.02790562,75.02790562,75.02790562,76.35581124,76.35581124,76.35581124,77.68371686,77.68371686,48.60466067,49.93256629,49.93256629,49.93256629,49.93256629,49.93256629,49.93256629,49.93256629,51.2604719,51.2604719,51.2604719,51.2604719,51.2604719,51.2604719,51.2604719,51.2604719,51.2604719,51.2604719,52.58837752,52.58837752,52.58837752,52.58837752,52.58837752,52.58837752,52.58837752,52.58837752,52.58837752,52.58837752,52.58837752,53.91628314,53.91628314,53.91628314,53.91628314,53.91628314,53.91628314,53.91628314,53.91628314,53.91628314,53.91628314,53.91628314,55.24418876,55.24418876,55.24418876,55.24418876,55.24418876,55.24418876,55.24418876,55.24418876,55.24418876,56.57209438,56.57209438,56.57209438,56.57209438,56.57209438,56.57209438,56.57209438,56.57209438,56.57209438,57.9,57.9,57.9,57.9,57.9,57.9,59.22790562,59.22790562,59.22790562,59.22790562,60.55581124,60.55581124,60.55581124,61.88371686,61.88371686,61.88371686,63.21162248,63.21162248]
Y=[82.04418876,83.37209438,84.7,86.02790562,87.35581124,80.71628314,82.04418876,83.37209438,84.7,86.02790562,87.35581124,88.68371686,90.01162248,78.0604719,79.38837752,80.71628314,82.04418876,83.37209438,84.7,88.68371686,90.01162248,91.3395281,76.73256629,78.0604719,79.38837752,80.71628314,82.04418876,83.37209438,87.35581124,88.68371686,91.12790562,92.45581124,93.78371686,93.78371686,91.12790562,93.78371686,95.11162248,92.45581124,93.78371686,95.11162248,96.4395281,91.12790562,92.45581124,95.11162248,96.4395281,97.76743371,80.50466067,81.83256629,91.12790562,95.11162248,96.4395281,97.76743371,99.09533933,80.50466067,96.4395281,97.76743371,99.09533933,96.4395281,97.76743371,99.09533933,95.11162248,97.76743371,99.09533933,95.11162248,96.4395281,97.76743371,95.11162248,96.4395281,97.76743371,96.4395281,78.02790562,79.35581124,78.02790562,79.35581124,71.38837752,82.01162248,83.3395281,84.66743371,72.71628314,74.04418876,75.37209438,76.7,82.01162248,83.3395281,84.66743371,74.04418876,75.37209438,76.7,78.02790562,79.35581124,83.3395281,84.66743371,85.99533933,74.04418876,75.37209438,76.7,78.02790562,79.35581124,80.68371686,84.66743371,85.99533933,74.04418876,78.02790562,79.35581124,80.68371686,82.01162248,74.04418876,80.68371686,82.01162248,83.3395281,80.68371686,82.01162248,83.3395281,84.66743371,82.01162248,83.3395281,84.66743371,80.68371686,82.01162248,83.3395281,84.66743371,80.68371686,82.01162248,83.3395281,79.35581124,80.68371686,58.34418876,59.67209438,55.68837752,57.01628314,58.34418876,59.67209438,66.31162248,54.3604719,55.68837752,57.01628314,67.6395281,53.03256629,54.3604719,55.68837752,67.6395281,53.03256629,54.3604719,55.68837752,57.01628314,53.03256629,54.3604719,55.68837752,57.01628314,58.34418876,53.03256629,54.3604719,55.68837752,57.01628314,58.34418876,51.70466067,53.03256629,57.01628314,58.34418876,51.70466067,53.03256629,58.34418876,70.29533933,51.70466067,53.03256629,58.34418876,53.03256629,57.01628314,46.27209438,42.28837752,43.61628314,44.94418876,46.27209438,47.6,48.92790562,50.25581124,40.9604719,42.28837752,43.61628314,44.94418876,46.27209438,47.6,48.92790562,50.25581124,51.58371686,52.91162248,40.9604719,42.28837752,43.61628314,44.94418876,46.27209438,47.6,48.92790562,50.25581124,51.58371686,52.91162248,54.2395281,42.28837752,43.61628314,44.94418876,46.27209438,47.6,48.92790562,50.25581124,51.58371686,52.91162248,54.2395281,55.56743371,42.28837752,43.61628314,44.94418876,46.27209438,47.6,51.58371686,52.91162248,54.2395281,55.56743371,40.9604719,42.28837752,46.27209438,47.6,51.58371686,52.91162248,54.2395281,55.56743371,56.89533933,40.9604719,46.27209438,47.6,54.2395281,55.56743371,56.89533933,39.63256629,40.9604719,54.2395281,55.56743371,39.63256629,40.9604719,55.56743371,52.91162248,54.2395281,55.56743371,54.2395281,55.56743371]

#绘制数据分布图
plt.scatter(X,Y, c = "k", marker='o', label='countries')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend(loc=2)
plt.show()

离散点绘图

DBSCAN

DBSCAN(Density-Based Spatial Clustering of Applications with Noise，具有噪声的基于密度的聚类方法)是一种很典型的密度聚类算法。

基本概念：

所需参数：

半径：Eps

Eps半径内指定的数目（阈值）：MinPts

 

数据点分为三：

1. 核心点：在半径Eps内含有超过MinPts数目的点
2. 边界点：在半径Eps内点的数量小于MinPts，但是落在核心点的邻域内
3. 噪音点：既不是核心点也不是边界点的点

 

概念：

1. Eps领域：半径Eps之内所有点的合集

2. 直接密度可达（密度直达）：核心点X1对Eps领域内的任意点都是直接密度可达

3. 密度可达：设数据点点序列p(1)，p(2)，p(3)，…，p(n)，其中p(1)是核心对象，p(2)是从p(1)出发直接密度可达，p(n)从p(1)出发是密度可达的

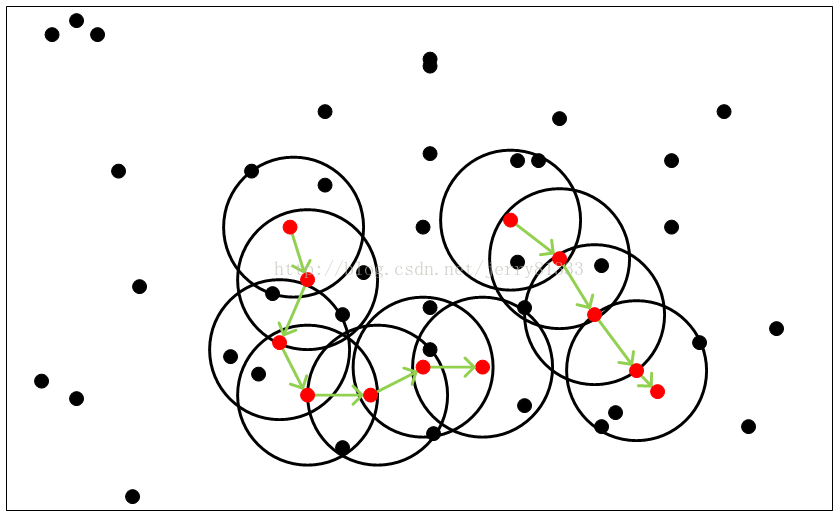
算法优点：

1. 不需要如同K-means一样设置初始类别个数

2. 可以对任意形状的稠密数据集进行聚类

3. 对噪点有抗性

4. 结果不会有偏倚（不是指每次结果完全一样，而是大部分相同，不排除个别点）

算法缺点：

1. 数据密度不均匀时难以使用

2. 样本集越大，收敛时间越长，可用K-D树进行优化

3. Eps，MinPts阈值难以界定，可用绘制k-距离曲线等方法界定

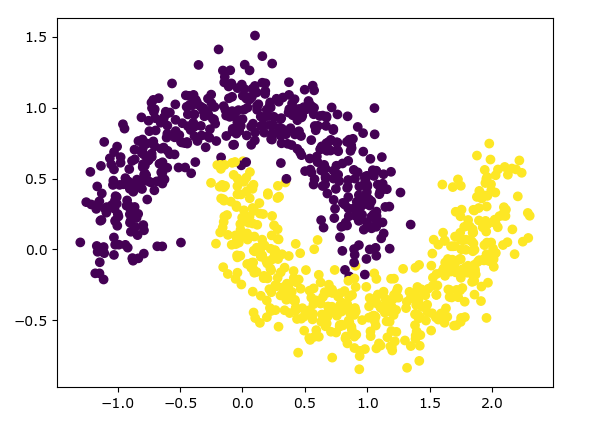
from sklearn.datasets.samples_generator import make_moons
import matplotlib.pyplot as plt
import time
from sklearn.cluster import KMeans
from sklearn.cluster import DBSCAN

X, y_true = make_moons(n_samples=1000, noise=0.15) #y_true是提前做绘图分类标识

plt.scatter(X[:, 0], X[:, 1], c=y_true)
plt.show()

# Kmeans
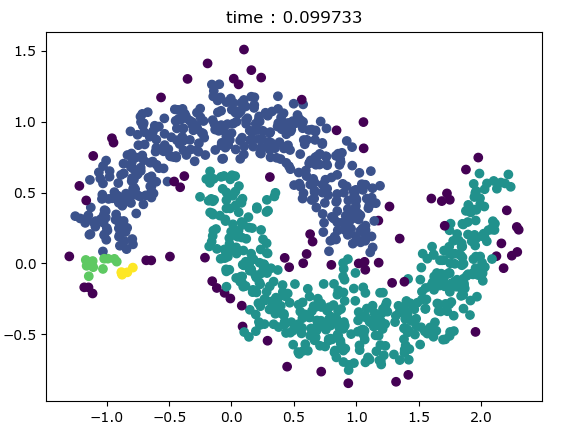
t0 = time.time()
kmeans = KMeans(init='k-means++', n_clusters=2, random_state=8).fit(X)
t = time.time() - t0
plt.scatter(X[:, 0], X[:, 1], c=kmeans.labels_)
plt.title('time : %f' % t)
plt.show()

# DBSCAN
t0 = time.time()
dbscan = DBSCAN(eps=.1, min_samples=6).fit(X)
t = time.time() - t0
plt.scatter(X[:, 0], X[:, 1], c=dbscan.labels_)
plt.title('time : %f' % t)
plt.show()

代码

原数据绘图

K-mean聚类绘图

DBSCAN聚类