java生产环境增量发版陷阱【原】

前言

在生产环境,我们为了降低发版风险,一般都只做增量发布,不做全量发布.

除非项目只有一到两人开发,对时间线和代码脉络结构一清二楚,才可全量发布.

然而增量发布也是有一定隐藏陷阱在里面的,以下就是笔者的项目组在增量迭代过程中一起遇上到陷阱

陷阱1 : 匿名内部类

如果修改的java源码中,有匿名内部类,那么最终在WEB-INF/classes/.......package....../Person.java 下面会生Person$XXX.class的匿名内部类,

但是我们在提交svn时,一般不涉及classes/下面的class文件的提交.

于是带来的问题是svn仅仅发现变更了源文件Person.java ,等到通过svn的记录都增量打jar包提交生产环境的时候. 经常会把Person$XXX.class匿名内部类给遗漏了.

导致上生产一般会报"类找不到"的异常.

解决方法:  参考我的另一篇文章  windows cmd命令 批处理bat 导增量jar包【原】

陷阱2 : 方法重载

和前一个问题有点相似,但不完全一样.

假如有以下两个java文件.

Test.java

package test;
import test.Person;

public class Test {
    public static void main(String[] args) {
        Person person = new Person();
        person.setId(18);
        person.setName("bobo");
        System.out.println(person.getId());
    }
}

Person.java

package test;

public class Person {
    int id = 0;
    String name = "";

    public int getId() {
        return id;
    }

    public void setId(int id) {
        this.id = id;
    }

    public String getName() {
        return name;
    }

    public void setName(String name) {
        this.name = name;
    }

}

现在把eclipse里面的Person.java的 id 属性从int 改成 Integer

package test;

public class Person {
    Integer id = 0;
    String name = "";

    public int getId() {
        return id;
    }

    public void setId(Integer id) {
        this.id = id;
    }

    public String getName() {
        return name;
    }

    public void setName(String name) {
        this.name = name;
    }

}

那么从源码Test.java的角度出发来讲,肉眼是看不出变化, 没错,源码还是源码. svn也不会发现变化.

但是! 其实 setId(int id) 和setId(Integer id) 这根本不是同一个方法, 这叫方法重载,在Person.java中本来就是可以并存的, 然而这个方法重载很特别, 因为int 和 Integer 是基本类型和对象类型互通的, 所以调用setId(18) 不管是用setId(int id) 还是 setId(Integer id)都可以 , 于是eclipse也不会报错, 其java文件还真是不需要修改的, 这就演变了成一个隐藏的陷阱, class早就发生变化了(eclipse 自动编译).

虽然java源码没变化,但所有调用到 Person对象的setId(Integer id)方法的class全发生变化了.所以这个时候增量发包的时候可能会很严重了,发生产后,隐藏的class(比如Test.class) 全没提交, 报一堆的java.lang.NoSuchMethodError异常. 这是笔者对Person变化前后用bccompare工具对Test.class文件作的二进制对比

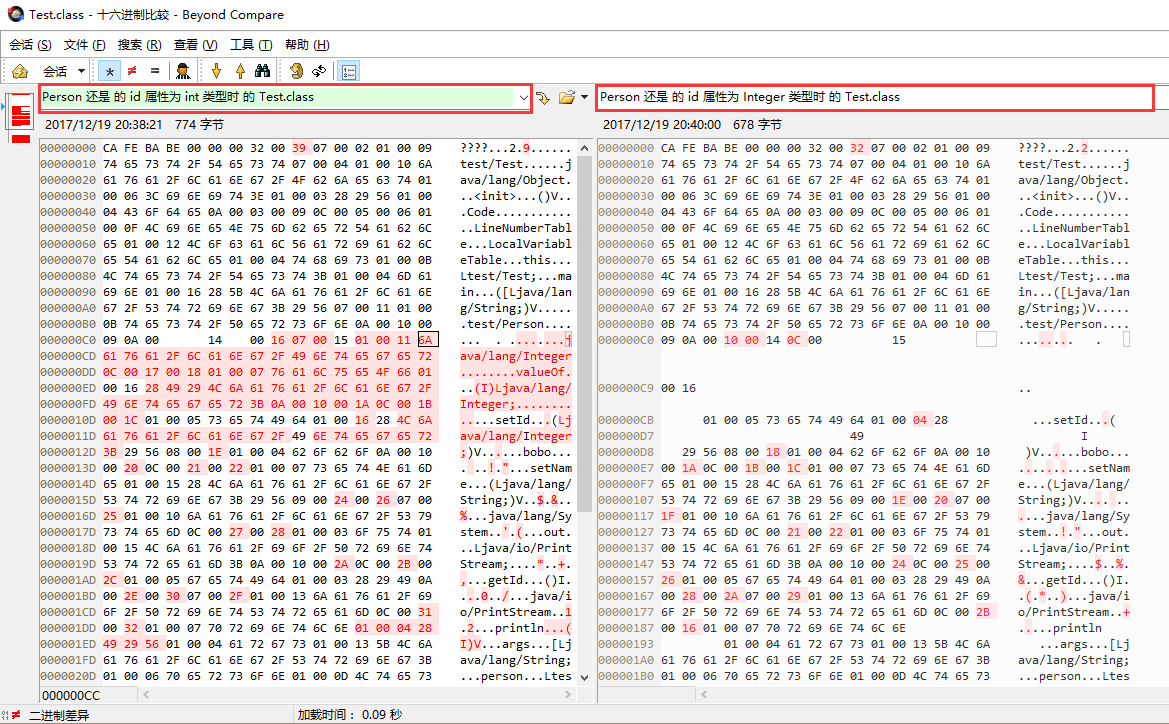
于此同时double 和 Double , float 和 Float 也都要特别小心方法重载时的其它调用类的底层class是否有变化.

 解决方案: 无 ! 只能向项目组强调 以 防患于未然 , 或者用 jenkin 等完善的自动化工具做全量发布。