Linux下R环境安装

R环境的两种安装方式，源码编译安装和yum在线安装

第一种：源码编译安装

1.首先，从官网上下载3.5.0版本

2.下载完后记得解压，我的习惯是解压在/usr/local下面

tar -zxvf R-3.5.0.tar.gz

3.然后，安装各种依赖环境

yum install -y gcc

yum install -y glibc-headers

yum install -y libreadline6-dev gfortran

yum install -y readline-devel

yum install -y wget libXt-devel

yum install -y fonts-chinese tcl tcl-devel tclx tk tk-devel

yum install -y mesa-libGLU mesa-libGLU-devel

yum install -y install bzip2-devel

yum install -y install xz-devel.x86_64

yum install -y install pcre-devel

yum install -y install libcurl

yum install -y install libcurl-devel

yum install -y  texinfo.x86_64

yum install -y texlive-pdftex-doc.noarch

yum install -y texlive

yum install gcc-gfortran

4.安装完依赖环境后，准备建立编译后的文件夹R 
    我习惯建立在usr中

mkdir /usr/local/R

5.接下来，进入R中，准备进行安装了。该R的安装是通过configure进行安装

cd /usr/local/R-3.5.0

./configure --enable-R-shlib=yes --with-tcltk --prefix=/usr/local/R

6.环境配置完毕后，可以进行make和安装了

make

make install

配置I5的话 大概是15到20分钟。

7.编译安装完毕后，进行环境配置

vim /etc/profile

R_HOME=/usr/local/R

PATH=$PATH:$R_HOME/bin

source /etc/profile

8.然后直接输入R回车就能进入R的控制台了

[root@siger-node2 local]# R

R下载安装
https://mirrors.tuna.tsinghua.edu.cn/CRAN/

RStudio下载安装
https://www.rstudio.com/products/rstudio/download/#download

第二种：yum在线安装

1.通过如下命令安装并启用 EPEL （如果已经安装过，直接执行第二步）

yum install epel-release

2.使用如下命令安装R

yum install R

3.安装完成之后，直接在终端输入R然后回车之后出现类似如下内容则表示安装成功

[root@siger-node1 local]# R

一， R语言所处理的工作层：

解释一下：

最下面的一层为数据源，往上是数据仓库层，往上是数据探索层，包括统计分析，统计查询，还有就是报告

再往上的三层，分别是数据挖掘，数据展现和数据决策。

由上图可知，R语言是可以用于数据挖掘，数据展现，而后领导根据展现的数据来决策，R语言在数据展现的方面，拥有很强大的功能。

二，R语言的数据结构：

包括如下的几项：包括向量，矩阵，数组，数据框，列表和因子

1，向量：

创建向量的方法一共有三种，分别如下：

第一种，使用c()的这个方法：

由于博客中木有R语言代码的选项，所以，下面选择截图：

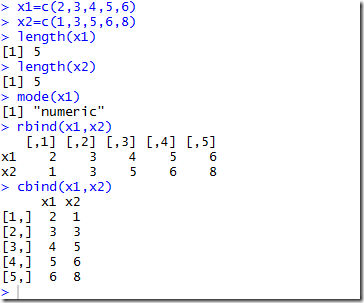
解释一下，就是创建x1向量，x2向量，然后分别使用length()和mode()函数，获得向量的长度和向量的类型，上面显示的向量的类型是numeric，即为数字类型。

然后，分别使用rbind(x1,x2)和cbind(x1,x2)两个方法分别对两个向量进行行组合和列组合。

那么向量是否可以为别的类型呢？答案很显然是可以的，如下所示，向量中只要含有字符串，那么这个向量就是字符类型的。

第二种创建向量的方法，及向量的截取：

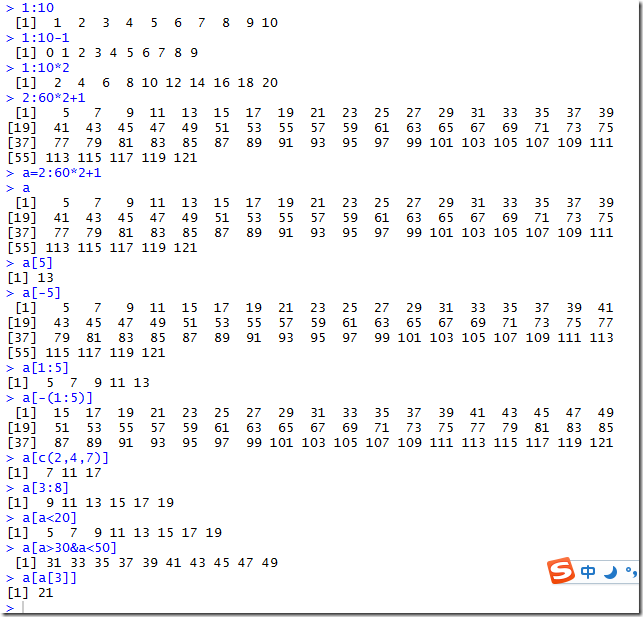
由上面的代码可知，不写c的情况下，可以直接使用“：”来完成向量的创建，而切在常见的同时，根据加减乘来决定所创建向量的具体的形式

向量中元素的选取和那啥别的语言中的数组的方法是相同的，不同的是，他可以加上一个负号进行选取，而后选取的结果就是去掉这个元素之后的其他的元素

这种方法不单单适用于单个元素，依旧适用于多个元素，多个元素的时候使用“：”来完成。

第三种创建向量的方式：

这种创建方式，长的和第一种方法有点相同，其效果和第二个方法的效果又有点相似，其中by其表示等差，，length表示的是个数，根据个数来判断方差到底是多少

这三种创建向量方法的总结对比，似乎会得到一个结论：

第一种，适合于创建有限个少量的元素的向量

第二种，适合于创建大量元素，但是这些元素之间关系不是那么强烈的向量

第三种，适合创建拥有等差性质的向量

下面的时候，还有一个创建向量的方法。。。。。

最后还有一个向量，是R语言之中内置的常向量，用来表示a,b,c,d...z等26个字母

2，使用特定的函数，对向量进行操作

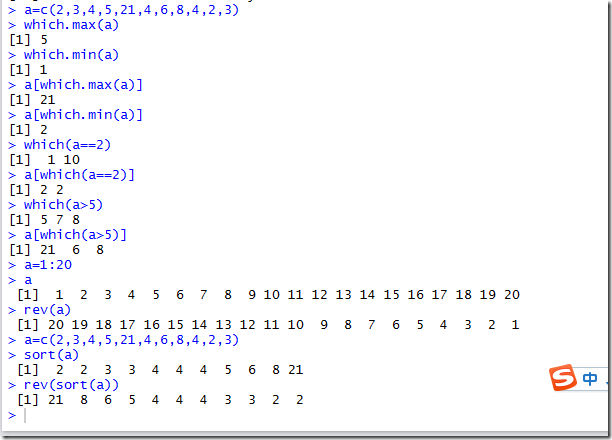
这里包括了which函数，其中which.max()和which.min()分别用来取向量中的最大值和最小值的下标，注意是下标，不是对应的值

还可以用来去特定范围和特定值的下标

而后便是rev()函数和sort()函数，分别用来进行反转和排序

2，矩阵

不同于创建向量的方法，矩阵的创建方法只有一种，且是在向量的基础上，对向量进行按列和按行进行排序得到的结果。

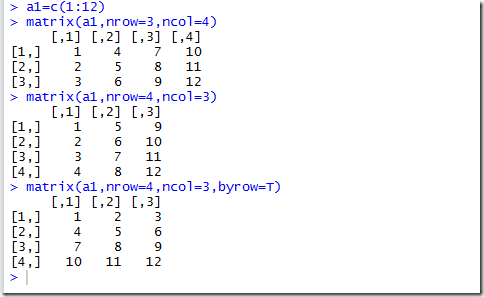
由上面可知，前面有关三个创建向量的方法是有误的，c（）方法很显然也可以用来创建大量的元素的向量

用matrix方法对向量进行组合的时候，默认是安装列来进行书序的组合，比如第一个，矩阵，按照列，第一个列是1,2,3，第二列才是4,5,6所以就是明显的按列进行，

如果改为用byrow=T，则改为按行来排列

3，数组

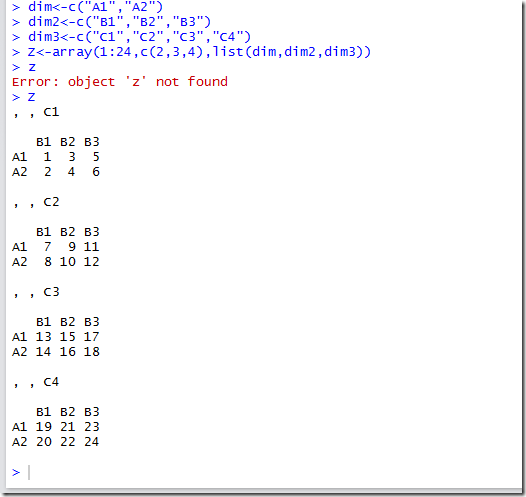
4， 数据框

数据框的构建也只有一种方法，他的也是有向量组合而成，由此可以见得，向量是R语言最根本对的数据结构，如果没有向量，一切都是不行的。

同时不同于矩阵，他的每一个列可以和其他的列是不同的类型

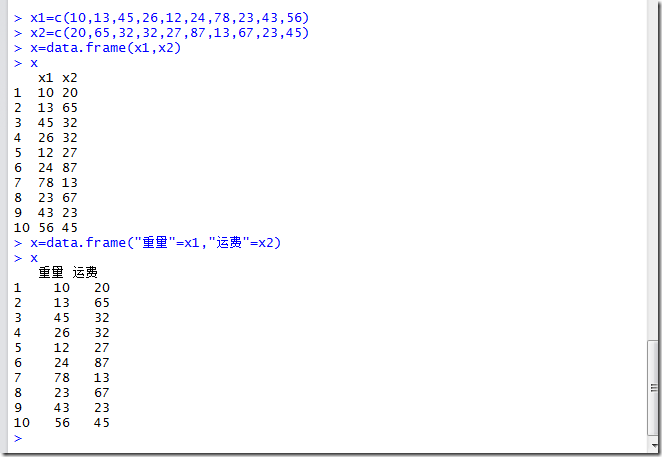
5，factor

下图所示，iris是R语言内置的数据框，如果使用facotor就可以选择其中的一列

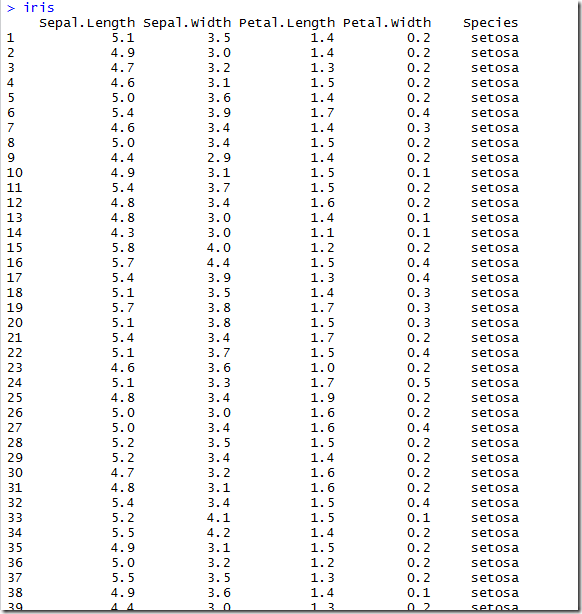
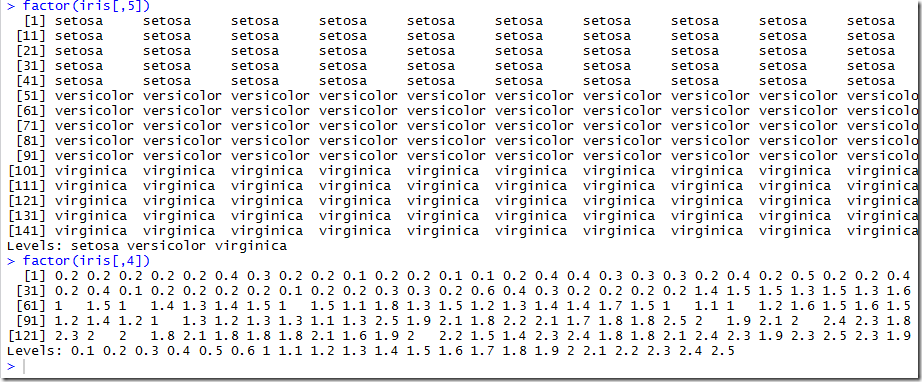
如上图所指示，就是去的列的值了，字面的上的意思就是取得影响因子，如果吧每一个当一个事物的特征值的话

6，列表

所谓列表，可以看成是有序个元素的集合，他存进去的顺序很显然是和取出来的书序是相等的。

三，R语言计算相关的函数：

普通运算：

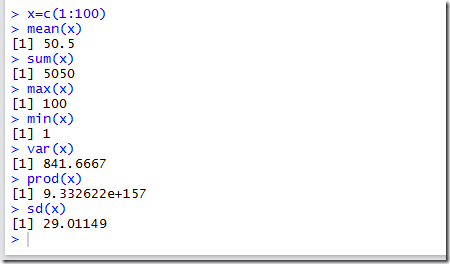
由上图所示，mean()是求平均值，sum（）是求和，max( ）是求最大值，，min()  是求最小值

---

矩阵运算，

包括加减乘除，求特征值和特征向量等等

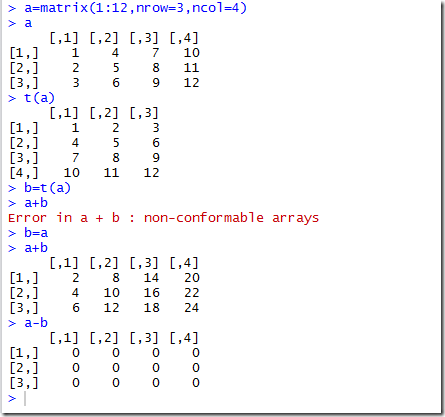
其加法减法的表示没有啥特殊的，同时需要注意的是，t()是表示转置，他的功效很大，还可以吧转化为矩阵，如下图所示：

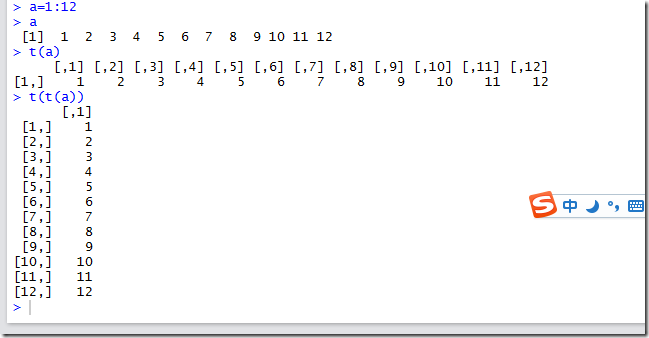
就完成了到行矩阵的转换，同时也完成了行矩阵到列矩阵的转换

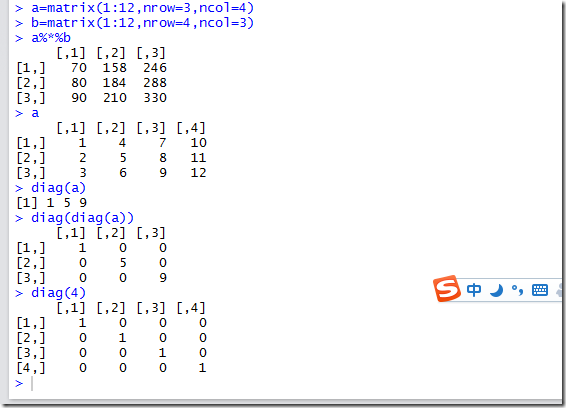
矩阵的乘法，就是%*%   ,纯粹的*只是矩阵的元素相乘。。

diag()函数，可以根据矩阵获得列表对象线上的元素，当然还可以根据对角线上的元素，来创建一个矩阵

同时可以用来构建单位阵

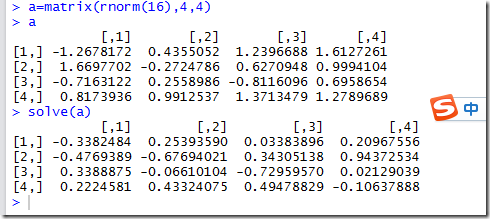
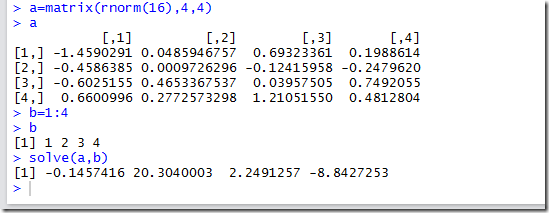
如下计算，rnorm是去的随机数，solve（）函数是用求得矩阵a的逆矩阵，即为矩阵的除法

如下图所示，solve函数依旧可以用来解方程组：

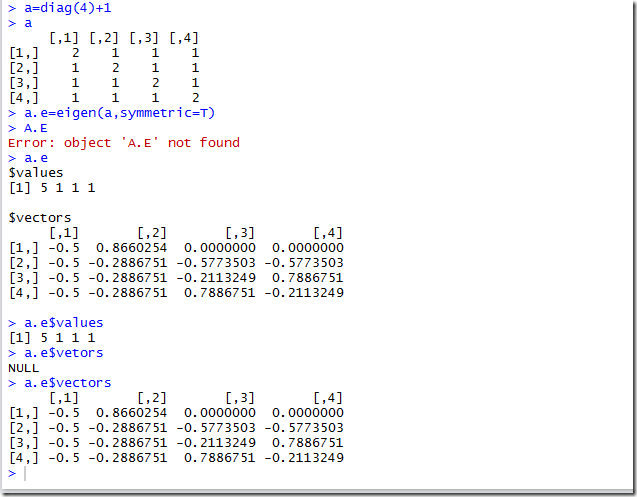
如下图所示，   eigen函数就是用来取得一个矩阵的特征向量和特征值，同时可以使用$来取出

四，R的语句：

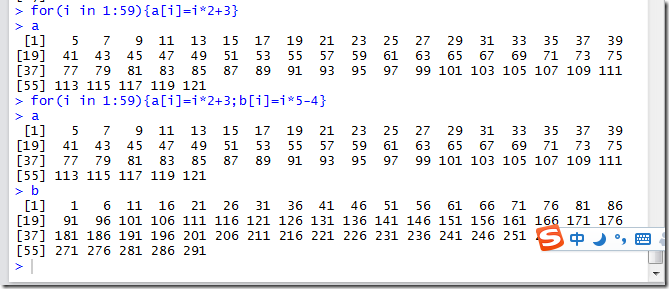
for语句：

不同于别的语法，for循环之中，没有必要初始化值，a或者b有一个初始化的值

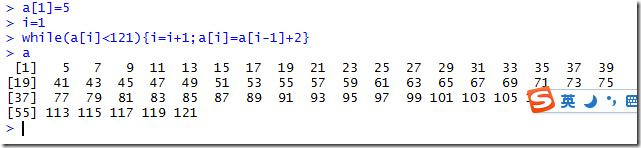
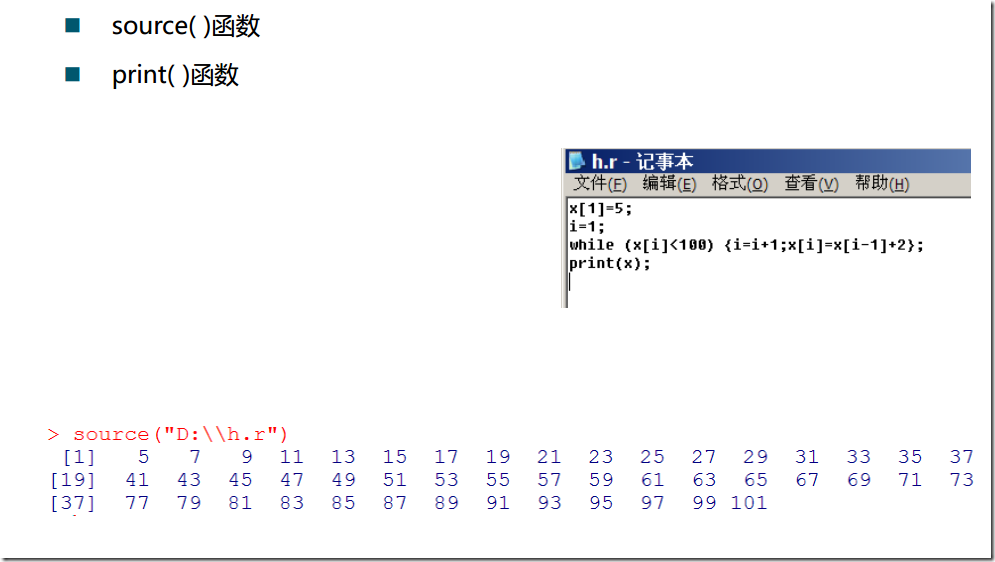
while 循环语句：

不同于上面的，a需要有初始的值，也还要控制i的加减

五，一些其他的特殊的函数：

注意在，文本中，如果想加载这个文件打印，就需要在文本的代码之中，使用print()函数。。。