OpenStack Manila发展动态系列--Austin峰会

1 Manila Mitaka版本概述

在Austin峰会上介绍到，Manila Mitaka发布版本Driver个数达到了18个，

M版本新加入14家公司（中国公司继华为之后又有99cloud等公司加入），

本版本完成了43个蓝图，主要的蓝图有共享迁移、将扩展API移入核心，

增加了功能测试、QoS公共特性支持、新增数据拷贝服务、

导入导出快照、增加了CephFS Native driver等等。

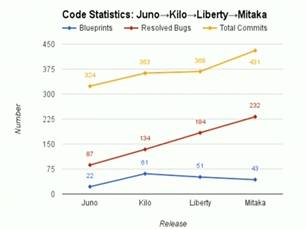
历史版本解决的bug、完成的蓝图、提交代码数量如下图所示。

2 Manila 企业应用

在谈到企业应用的时候说到，低成本，异构基础架构是Manila的优势。

并且填补了OpenStack中文件共享服务管理的空白。其中介绍了几个应用案例：

比如manila与docker结合，为docker提供文件共享管理服务。

Manila功能与Sahara的集成，可使用Manila共享为Sahara存储工作模板，在Sahara用文件共享写入和写出数据。

Sahara用户可通过Sahara服务调用Manila API接口完成自动挂载NFS共享功能。

Manila提供分布式文件系统（HDFS）等等。

Manila在SUSE OpenStack Cloud 6 中完全支持，

并且在SUSE OpenStack Cloud 6中演示了集成的Manila的功能。

3 Manila Newton版本规划

对于Manila下一个Newton版本的规划，主要包括增加快照相关功能，

支持share servers的复制，完善share迁移，

通用组取代一致性组（兼容复制组、迁移组、CGs），容器驱动，Active-Active HA等等。

详细信息如下：

1） Manila新增2个快照功能：一个是新增自动挂载只读快照功能，用于快速恢复微小的改动，比如恢复共享中的一个文件。

为了避免快照与快照的父共享访问权限的冲突，

增加了类似Share ACL的一套API控制快照权限，即可以单独为快照设置访问权限。

另一个是新增快照回滚功能，用于源共享的快速恢复，

有些不支持从快照创建共享（create share from snapshot）的后端可以用这个功能代替。

由于后端阵列实现快照回滚必须删除回滚快照时间点以后的快照。因此暂时支持允许回滚到最近时间点的快照。

2）增加了per-share-type quotas功能，即对每个share type都可以配置share容量、个数等配额信息。

这是由运营商提出来的特性，希望通过对share type配额的配置进行share容量限制以控制成本。

3）提醒各Driver使用update access接口替换原有的allow_access、deny_access接口。

以便manila中对ACL进行批量原子操作。

4）为了解决Active-Active HA应用、API请求竞争（即在没有数据库层面的并发控制时，管理的资源可能被不同的API修改），

引入分布式锁（Zool），解决manila各个服务间操作冲突的问题。在Cinder中也引入了分布式锁，目前正在代码review阶段。

5） Manila添加版本对象（version object），即将当前使用的SQLAlchemy objects抽象成manila objects，

使用对象代码和实际的数据库架构隔绝，更容易滚动升级等。

6）计划实现share类型更新功能（retype）。

Manila retype含义即对共享类型（share type）的更新。

比如，对于Huawei存储的共享类型从Thin到Thick的转换，

如果涉及到不同后端的操作比如从Huawei到Ceph，

retype功能会调用迁移功能自动将源共享迁移到符合条件的后端上创建的新共享。

7） Data Service Helper为Driver提供数据相关的的标准化操作，

比如share数据拷贝（create share from snapshot）、

获取数据拷贝进度、取消数据拷贝、由Driver指定功能的回调函数等等。

8）为了解决Manila中一致性组（Consistency groups）、复制、迁移特性都可能存在对share组的操作，

但是不同特性之间的share组的概念怎么融合的问题。

比如在实际操作中我们会存在复制一致性组、快照复制组、迁移一个复制组、

备份一个一致性组、备份一个复制组。社区希望通过一个统一的API和尽可能小的变化的用户体验来整合这些组。

因此引入了通用组概念来解决这一问题，不同于一致性组，不需要保证share group任何专业化的操作。

当然，功能丰富的后端想增加自己的秘密武器，无论是CGs，基于组的复制，或任何其他可能会更容易。

最后由于时间原因Austin峰会上提出的Manila的议题并没有讨论完成，敬请关注后续的相关系列文章。

编者注：本文来自OpenStack开源团队工程师钟君