DNA序列对齐问题

一、问题描述

该问题在算法导论中引申自求解两个DNA序列相似度的问题。

可以从很多角度定义两个DNA序列的相似度，其中有一种定义方法就是通过序列对齐的方式来定义其相似度。

给定两个DNA序列A和B，对齐的方式是将空格分别插入到A和B序列中，得到具有相同长度的对齐后的序列C和D；空格可以插入到任意的位置（包括两端），但是相同位置不能同时为空格，也即是不存在C[i]和D[i]同时为空格的情况。然后为对齐后的序列的每个位置打分，总分为每个位置得分之和，具体的打分规则如下：

a、如果C[i] == D[i]且都不是空格，得3分；

b、如果C[i] != D[j]且都不是空格，得1分；

c、如果C[i] 或者D[i]是空格，得0分。

求给定原序列A和B的一个对齐方案，使得该对齐方案的总分最高。

例如，序列原序列A和B如下：

        String strA = "GATC";
        String strB = "ATCG";

则其中一个对齐方案如下：

GATC*
*ATCG

该方案总得分score=2*0+3*3 = 9分。

实际上这是最优的对齐方案，在所有的对齐方案中总得分最高为9分。

二、问题分析

为了用更加简单的方式来表示对齐的方案，我们尝试用一些特定的字符记号来表示对齐方案，对此，首先做一个约定，对于打分规则：

1、情况a用“=”字符标记；

2、情况b用“~”字符标记；

3、情况c用“*”字符标记，但是情况c实际上可以细分为两种情况：C[i]为空格时用“+”标记，D[i]为空格时用“-”号标记。这样用“+”和“-”细分的表示相比于统一用“*”来表示，本质的区别在于让对齐方案具有所谓的“方向性”，后面会看到这样的细分对于算法的实现有一定的好处。

有了这样的约定，可以将一个对齐方案用这些字符表示出来，该字符串称之为一个对齐规则字符串R。

例如上面的例子中，对齐规则就可以用字符串“-===+”来表示。

可以推断，任何两个原序列的对齐规则字符串R的长度必然满足：

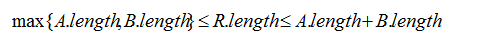
只要能够求得最优对齐方案的对齐规则字符串，就可以计算出最高分数，还可以还原出各自的对齐序列。

考察该问题的最优子结构性质，与最长公共子序列思考的角度比较类似，

用C(i,j)表示序列A[0]...A[i]和序列B[0]...B[j]的最优对齐方案的得分，不难得出其初始条件和递推求解式：

用R(i,j)表示序列A[0]...A[i]和序列B[0]...B[j]的最优对齐方案的对齐规则字符串，结合上面的递推求解式，不难推出对齐规则字符串的运算规则：

三、算法实现

package agdp;
public class Alignment {
    //根据对齐骨规则生成相应的对齐后的字符串
    private static String[] generate(String base,String ...origin){
        int num = origin.length;
        String[] align = new String[num];
        for (int i = 0; i < num; i++) {
            if (origin[i].length() == base.length()) {
                align[i] = origin[i];
            }else {//base.length()只能是等于或者大于两个原字符串的长度
                String tmp = "";
                for (int j = 0,k = 0; j < base.length(); j++) {
                    if (base.charAt(j) == '+') {
                        if (i == 0) {tmp = tmp+"*";}
                        else{tmp = tmp+origin[i].charAt(k++);}
                    }else if(base.charAt(j) == '-'){
                        if (i == 0) {tmp = tmp+origin[i].charAt(k++);}
                        else{tmp = tmp+"*";}
                    }
                    else {
                        tmp = tmp+origin[i].charAt(k++);
                    }
                }
                align[i] = tmp;
            }
        }
        return align;
    }
    public static String align(String strA,String strB){
        int m = strA.length(),n = strB.length(),tmp;
        //aux数组记录子问题的最有对齐方案的分数，也即子问题的最高分数。
        int[][] aux = new int[m+1][n+1];
        //rule数组记录对齐方案，分别用"+"、"-"、"="和"~"记录四种情况。
        String[][] rule = new String[m+1][n+1];
        //rule初始化
        rule [0][0] = "";
        for (int i = 1; i < m+1; i++) {
            rule[i][0] = rule[i-1][0]+"-";
        }
        for (int i = 1; i < n+1; i++) {
            rule[0][i] = rule[0][i-1]+"+";
        }
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (strA.charAt(i-1) == strB.charAt(j-1)) {
                    aux[i][j] = aux[i-1][j-1]+3;
                    rule[i][j] = rule[i-1][j-1] + "=";//A[i]==B[j]：->"="
                }else {
                    tmp = Math.max(Math.max(aux[i-1][j], aux[i][j-1]), aux[i-1][j-1]+1);
                    aux[i][j] = tmp;
                    if (tmp == aux[i-1][j-1]-1) {//A[i]!=B[j]且A[i]和    B[j]不为空字符：->"~"
                        rule[i][j] = rule[i-1][j-1]+"~";
                    }else if(tmp == aux[i-1][j]-2){//B[i]为空字符:->"-"
                        rule[i][j] = rule[i-1][j]+"-";
                    }else{
                        rule[i][j] = rule[i][j-1]+"+";//A[i]为空字符:->"+"
                    }
                }
            }
        }
        //格式化输出aux数组
        for (int i = 0; i < m+1; i++) {
            for (int j = 0; j < n+1; j++) {
                System.out.format("%3d",aux[i][j]);
            }
            System.out.println();
        }
        //格式化输出rule数组
        for (int i = 0; i < m+1; i++) {
            for (int j = 0; j < n+1; j++) {
                System.out.format("%-15s",rule[i][j]);
            }
            System.out.println();
        }
        //返回最优的对齐方法对应的规则
        return rule[m][n];
    }
    //根据规则字符串计算分数
    public static int getScore(String ruleStr){
        int score = 0;
        for (int i = 0; i < ruleStr.length(); i++) {
            if (ruleStr.charAt(i) == '=') {
                score += 3;
            }else if (ruleStr.charAt(i) == '~') {
                score += 1;
            }
        }
        return score;
    }
    public static void main(String[] args) {
        // TODO Auto-generated method stub
        int[] scoreAry = {3,1,0,0};
//        String strA = "GATCGGCAT";
//        String strB = "CAATGTGAATC";
        String strA = "GATC";
        String strB = "ATCG";
//        String strA = "GAC";
//        String strB = "ATCG";
        String ruleStr = align(strA, strB);
        System.out.println(ruleStr);
        int score = getScore(ruleStr);
        System.out.println(score);
        String[] alignStr = generate(ruleStr, strA,strB);
        for(String str:alignStr){
            System.out.println(str);
        }
    }
}

还是以原始序列“GATC”和“ATCG”为例：

其子问题的得分的计算如下：

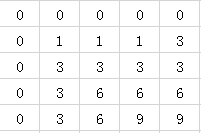
子问题的对齐规则字符串的计算如下：

需要特别注意的是，用“+”和“-”号来区分打分情况c后，对齐规则字符串是具有“方向性”的，也就是说对齐规则“-===+”是指从A->B方向的对齐规则。那如果需要B->A的对齐规则，只需要将对齐规则的字符串中+“和”-”相互替换即可。

实际上，从DNA序列对齐问题过渡到编辑距离问题是很比较自然的。本文也有意识的将这两个问题联系在一起，编辑距离问题见下一篇博文。

参考资料：

算法导论.第十五章 习题15-5

转载请注明原文出处：

http://www.cnblogs.com/qcblog/p/7820140.html