一、二次假设

实际上线性假设的复杂度是受到限制的，

需要高次假设打破这个限制

假设数据不是线性可分的，但是可以被一个圆心在原点的圆分开，

需要我们重新设计基于该圆的PLA等算法吗

不用，

只需要通过非线性转换将X域圆形可分变为Z域线性可分

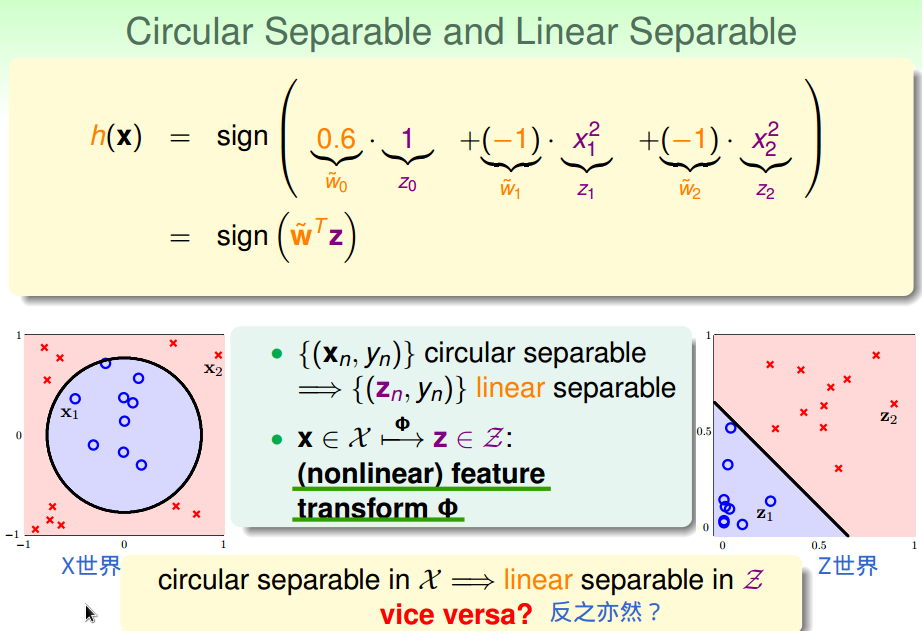
通用的二次假设集

二、非线性转换

好的二次假设

非线性转换的步骤

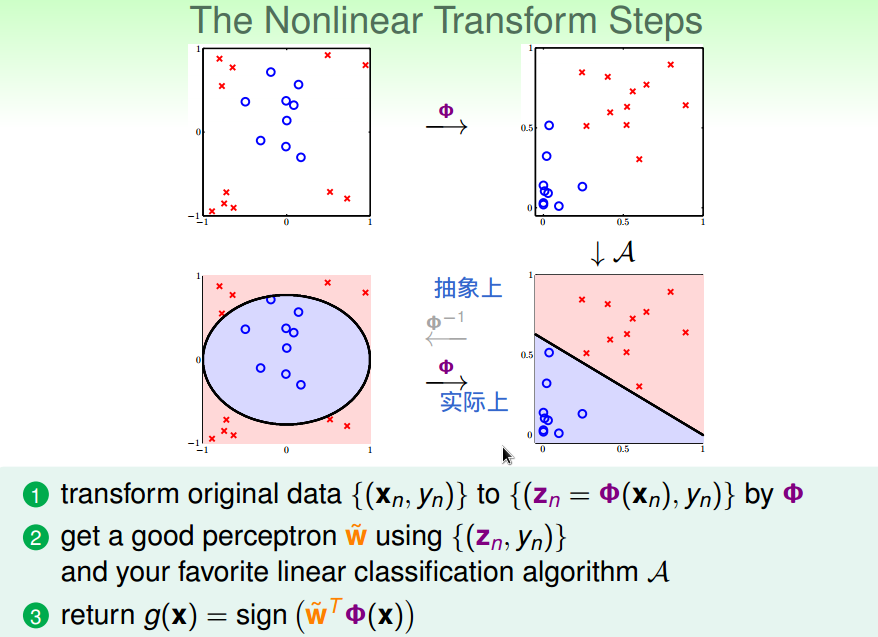
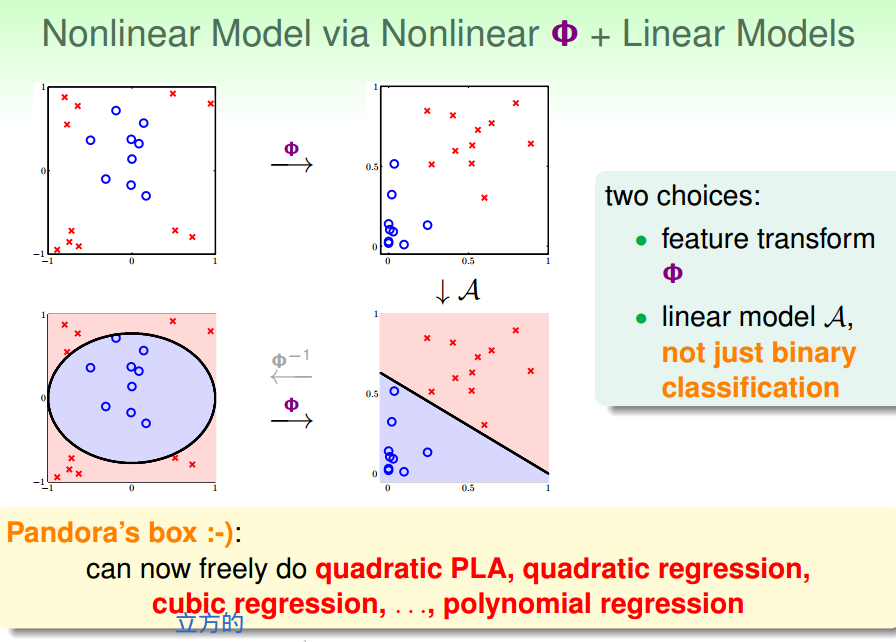
三、非线性转换的代价

计算/存储代价

次数越高，代价越大

模型复杂度代价

次数越高，代价越大

高次假设能使样本内代价值更小；

低次假设能保证泛化误差更小

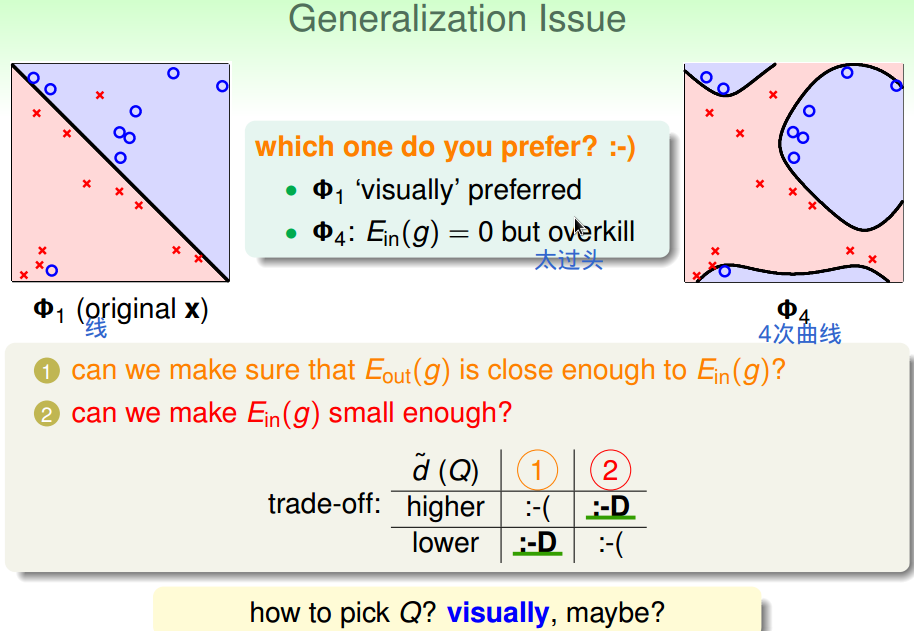
可视化数据后再选择：

一是数据维度高时难以可视化；

二是可视化后再选择实际上人脑里产生的模型复杂度代价并没有算进去，

加上后实际代价不一定很低

、

四、结构化假设集

低价假设集合是包含在高次假设集合中的

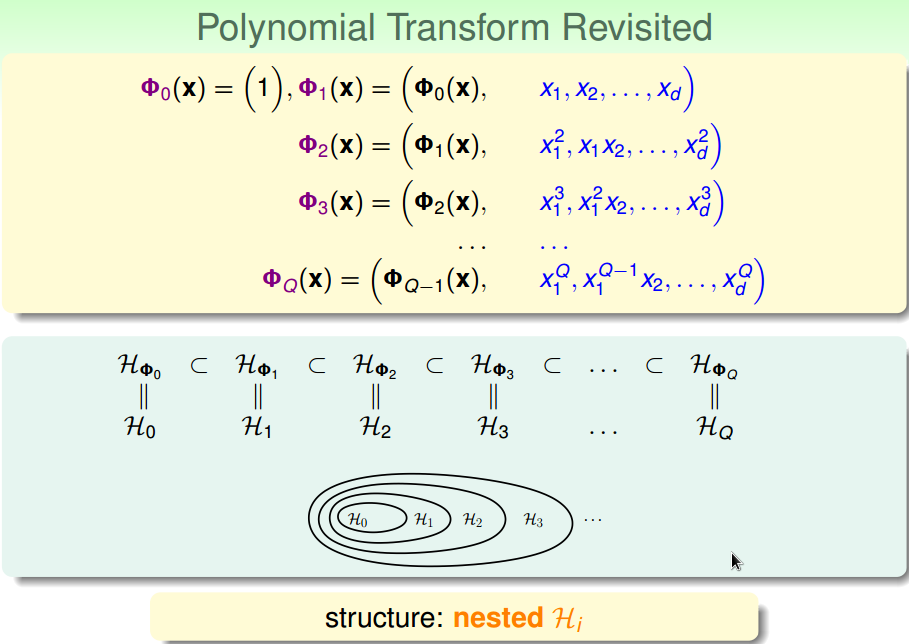
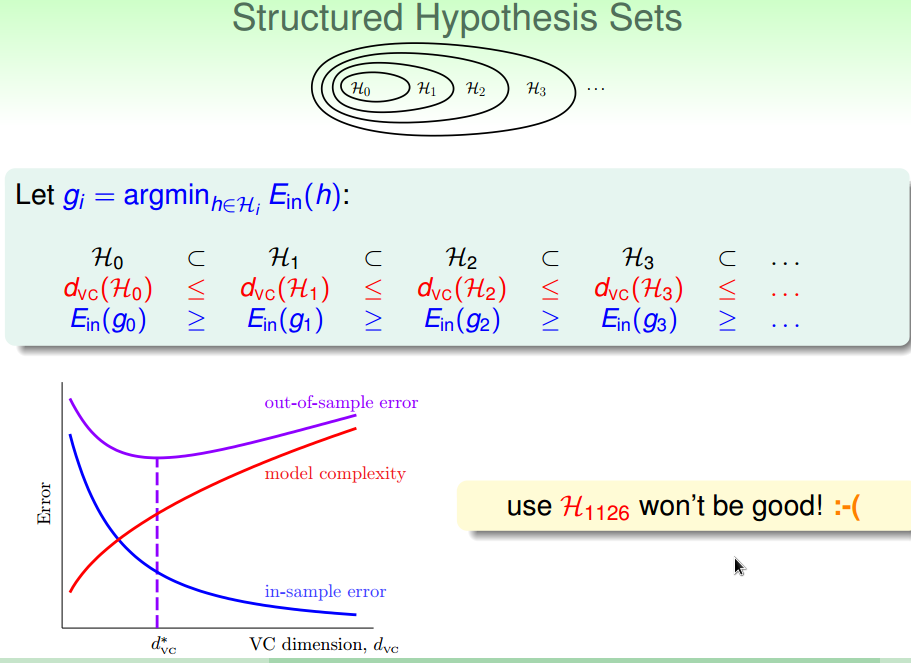
先线性模型，效果不好的话，再使用更高次点的模型

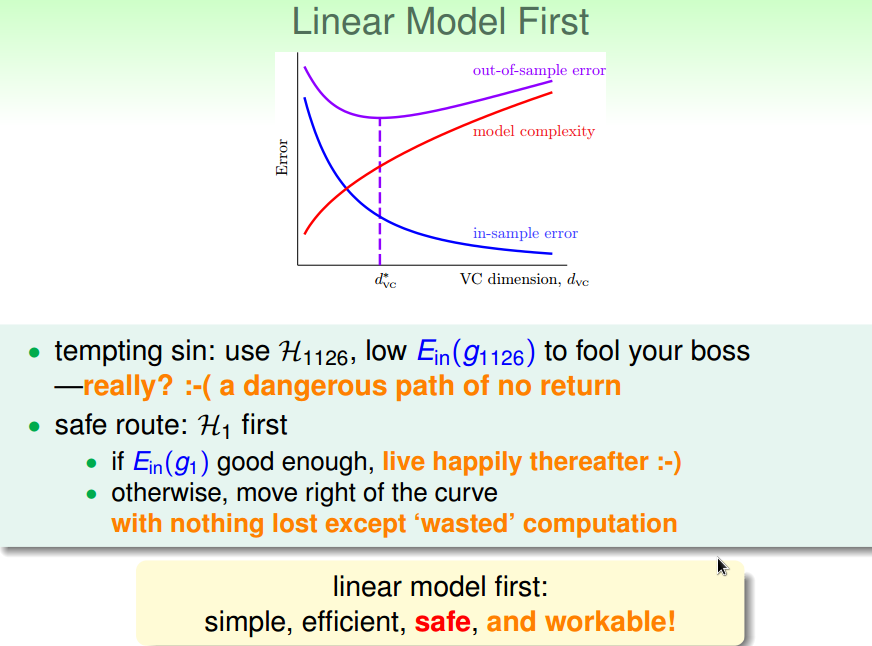
12 Nonlinear Transformation的更多相关文章

  1. 机器学习基石笔记：12 Nonlinear Transformation

    一.二次假设 实际上线性假设的模型复杂度是受到限制的, 需要高次假设打破这个限制. 假设数据不是线性可分的,但是可以被一个圆心在原点的圆分开, 需要我们重新设计基于该圆的PLA等算法吗? 不用, 只需 ...

  2. 特征的非线性变换（Feature Non-linear Transformation）

    有时候特征x和目标y不呈线性关系,线性模型y=wx+b不能很好地反映事物的规律或者无法对事物进行有效分类,因此此时我们需要使用非线性模型. (x=([x1,x2,...,xn])T,w=([w1,w2 ...

  3. Coursera台大机器学习课程笔记11 -- Nonlinear Transformation

    这一节讲的是如何将线性不可分的情况转为非线性可分以及转换的代价.特征转换是机器学习的重点. 最后得出重要的结论是,在做转换时,先从简单模型,再到复杂模型. 参考:http://www.cnblogs. ...

  4. ApacheCN 人工智能知识树 v1.0

    贡献者:飞龙 版本:v1.0 最近总是有人问我,把 ApacheCN 这些资料看完一遍要用多长时间,如果你一本书一本书看的话,的确要用很长时间.但我觉得这是非常麻烦的,因为每本书的内容大部分是重复的, ...

  5. ApacheCN 机器学习译文集 20211111 更新

    台湾大学林轩田机器学习笔记 机器学习基石 1 -- The Learning Problem 2 -- Learning to Answer Yes/No 3 -- Types of Learning ...

  6. 可视化MNIST之降维探索Visualizing MNIST: An Exploration of Dimensionality Reduction

    At some fundamental level, no one understands machine learning. It isn’t a matter of things being to ...

  7. RGB,CMYK,HSB各种颜色表示的转换 C#语言

    Introduction Why an article on "colors"? It's the same question I asked myself before writ ...

  8. 高效的多维空间点索引算法 — Geohash 和 Google S2

    原文地址:https://www.jianshu.com/p/7332dcb978b2   引子 每天我们晚上加班回家,可能都会用到滴滴或者共享单车.打开 app 会看到如下的界面:     app ...

  9. Effective Tensorflow[转]

    Effective TensorFlow Table of Contents TensorFlow Basics Understanding static and dynamic shapes Sco ...

随机推荐

  1. multisim&proteus&protel比较

    Multisim有超强板级的模拟/数字电路板的设计工作.它包含了电路原理图的图形输入.电路硬件描述语言输入方式,具有丰富的仿真分析能力.高版本可 以进行单片机等MCU的仿真.Multisim有实际元器 ...

  2. Jmeter之解决烦人的中文乱码问题

    Jmeter是一款国外开源工具,所以就跟LR一样,对中文的支持不是很好,经常会有同学录制脚本后回放或者是发送HTTP请求,看到响应报文里面有乱码! 那如何才能解决这个问题呢?我们分2个情况来分析: 一 ...

  3. Android-Error3：Error when loading the SDK

    解决方法: 用C:\android\sdk\tools中的devices.xml将出现错误的地方的devices.xml替换掉既可以了.

  4. 程序员也是弱势群体？——从WePhone开发者事件说起

    作为一名不爱凑热闹的人,今天一直在持续关注一个热点事件--WePhone开发者自杀,即使前几天热议的孕妇跳楼新闻我都不太关注,但是这个事件却让我深深的震撼,花了几个小时在微博上搜索了相关的信息,去了解 ...

  5. 10个经典的Java面试题集合（转载）

    1.Java的HashMap是如何工作的? HashMap是一个针对数据结构的键值,每个键都会有相应的值,关键是识别这样的值. HashMap 基于 hashing 原理,我们通过 put ()和 g ...

  6. (5)ES6解构赋值-函数篇

    函数参数的解构赋值 function sum(x, y) { return x + y; } sum(1,2); //解构赋值 function sum([x, y]) { return x + y; ...

  7. (1)ES6中let,const,对象冻结，跨模块常量，新增的全局对象介绍

    1.let声明变量,var声明变量,而const声明的常量 2.let与var的区别 let可以让变量长期驻扎在内存当作 let的作用域是分块[ {快1  {快2 }  }每个大括号表示一个独立的块 ...

  8. Flask05 cookie

    1 什么是cookie 就是网站存放到你浏览器中的一部分固定内容:当你下次访问我这个网站的时候,你会把之前我存放到你浏览器中的数据带回来给我        你要先登录(用户名.密码) ->   ...

  9. java四则运算

    题目描述: 从<构建之法>第一章的 "程序" 例子出发,像阿超那样,花二十分钟写一个能自动生成小学四则运算题目的命令行 "软件",满足以下需求: 除 ...

  10. 结对编程1---四则运算---GUI

    201421123003 黄建英 201421123004 黄美海 题目描述: 我们在个人作业1中,用各种语言实现了一个命令行的四则运算小程序.进一步,本次要求把这个程序做成GUI(可以是Window ...