[UPC10525]:Dove打扑克（暴力+模拟）

题目描述

　　$Dove$和$Cicada$是好朋友，他们经常在一起打扑克来消遣时光，但是他们打的扑克有不同的玩法。
　　最开始时，牌桌上会有$n$个牌堆，每个牌堆有且仅有一张牌，第$i$个牌堆里里里那个扑克牌的编号为$i$，任意两张牌仅有标号不不同。游戏会进行$m$轮，每轮$Dove$可以执行行下列操作之一：
　　$\bullet 1\ x\ y$，将编号为$x,y$的牌所在的牌堆合并，如果此时$x,y$已在同一牌堆中，那么不进行任何操作。
　　$\bullet 2\ c$，询问有多少对牌堆的牌数之差不少于$c$。形式化的，对于当前的$r$个牌堆中，有多少对$i,j(i<j)$，满足$|size_i-size_j|\geqslant c$，其中$size_i$表示第$i$个牌堆的牌数。
　　每次$Cicada$都不能很快的回答出$Dove$的询问，为了不让$Cicada$难堪，$Dove$想要写一个小程序来帮助$Cicada$，但是$Dove$还要把妹学高考，所以这个任务就交给你啦！

---

输入格式

　　第一行两个空格隔开的整数$n,m$。
　　接下来$m$行，每行为$1\ x\ y$或者$2\ c$，具体含义如上文所示。

---

输出格式

　　对于每个询问，输出一行一个整数表示答案。

---

数据范围与提示

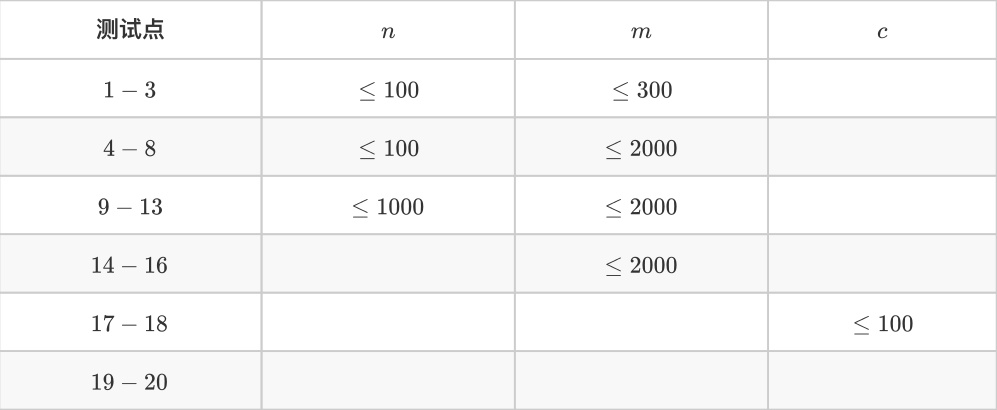
$n,c\leqslant 10^5,m\leqslant 3\times 10^5$

---

题解

显然答案就是$\sum \limits_{i=1}^ns[i]\times s[<(i-c)]$，其中$s[i]$表示有$i$个石子的堆的个数。

用树状数组即可快速求出$s[<(i-c)]$，由于同时最多只会有$\sqrt{n}$个不同的$s[i]$，于是去个重就好了。

时间复杂度：$\Theta(n\sqrt{n}\log n)$。

期望得分：$100$分。

实际得分：$100$分。

---

代码时刻

#include<bits/stdc++.h>
using namespace std;
int n,m,t;
int fa[100001],bl[100001],size[100001],num[100001];
long long ans[2][100001];
vector<int> vec;
int find(int x){return fa[x]==x?x:fa[x]=find(fa[x]);}
void change(int x,int w){ans[0][x]+=w;ans[1][bl[x]]+=w;}
void del(int x)
{
	if(x<=t)num[x]--;
	else vec.erase(lower_bound(vec.begin(),vec.end(),x));
	for(int i=1;i<=t;i++)change(abs(x-i),-num[i]);
	for(auto i:vec)change(abs(x-i),-1);
}
void add(int x,int y)
{
	for(int i=1;i<=t;i++)change(abs(size[x]-i),num[i]);
	for(auto i:vec)change(abs(size[x]-i),1);
	if(size[x]<=t)num[size[x]]++;
	else vec.insert(lower_bound(vec.begin(),vec.end(),size[x]),size[x]);
}
long long ask(int x)
{
	long long res=0;
	for(int i=x;i<=bl[x]*t;i++)res+=ans[0][i];
	for(int i=bl[x]+1;i<=bl[n];i++)res+=ans[1][i];
	return res;
}
int main()
{
	scanf("%d%d",&n,&m);
	t=sqrt(n);
	for(int i=1;i<=n;i++)
	{
		fa[i]=i;
		size[i]=1;
		bl[i]=(i-1)/t+1;
	}
	num[1]=n;ans[0][0]=ans[1][0]=1LL*n*(n-1)/2;
	while(m--)
	{
		int opt;scanf("%d",&opt);
		switch(opt)
		{
			case 1:
				int x,y;
				scanf("%d%d",&x,&y);
				x=find(x);y=find(y);
				if(x==y)continue;
				del(size[x]);
				del(size[y]);
				size[x]+=size[y];
				fa[y]=x;
				add(x,y);
			break;
			case 2:
				int c;scanf("%d",&c);
				printf("%lld\n",ask(max(c,0)));
			break;
		}
	}
	return 0;
}

---

rp++