问题 L: 超超的中等意思

问题 L: 超超的中等意思

时间限制: 1 Sec  内存限制: 128 MB
提交: 366  解决: 27
[提交] [状态] [命题人:jsu_admin]

题目描述

已知p,q,k和一个难搞得多项式(px+qy)^k。想知道在给定a和b的值下计算多项式展开后x^a*y^b得系数s。

输入

多组输入，每组数据一行输入p,q,k,a,b。其中保证k = a+b，所有输入都为非负数且不大于50000

 

 

输出

输出系数s对2^61-1取模后的值

样例输入 Copy

1 1 2 1 1

样例输出 Copy

2

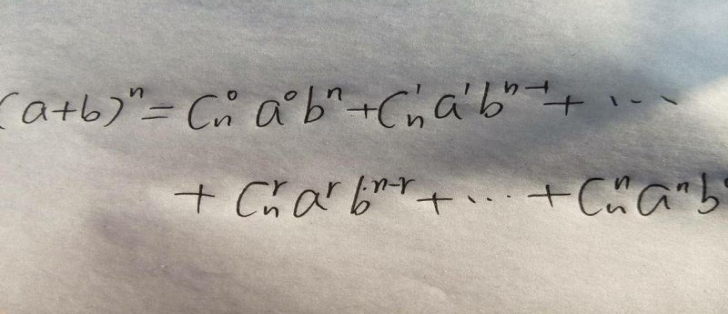
式子我们很容易就可以得知我们要求的是那个系数， 答案也就是求 组合数*x 的系数的 a 次方*y 的系数的 b 次方，

根据这个

我们在计算次方的时候可以用快速幂节约时间，组合数也可以由     C（m+1,n+1）

=C(m,n)+C(m+1,n)递推打表

 #include<iostream>
 #include<cmath>
 //using namespace std;
 //#include <iostream>
 #include<string.h>
 #include <stdio.h>
 #define ll long long
 typedef __int128 lll;
 const lll MOD = ;
 using namespace std;
 const int N = ;
 lll nn[N],mm[N];

  lll dp[][];
 void D()
 {
   lll n, k;
     dp[][] = ;
     for(int i = ; i < ; i++)
     {
         dp[i][] = ;
     }
     for(int i = ; i < ; i++)
     {
         for(int j = ; j <= i; j++)
             dp[i][j] = dp[i - ][j] + dp[i - ][j - ];
     }
     //int n, k;
     //while(scanf("%d %d", &n, &k) == 2)
    // {
         //printf("%d\n", dp[n][k]);
    // }
    return ;
   //  return 0;
 }
 lll C(lll n,lll m)
 {
     if(m==||n==m) return ;
     lll sb=min(m,n-m);
     lll f=,f1;
     for(lll i=;i<=sb;i++)
     {
         f1=f*(n-i+)/(i);
         f=f1;
     }
     return f1;
 }
 lll pow64(lll x, lll y) {

     if(!y) return ;
     if(x >= MOD) x %= MOD;
     lll ans = ;
     while(y) {

         if(y & ) ans = ans * x % MOD;
         x = x * x % MOD;
         y >>= ;

     }
     return ans;

 }
 int main()
 {
     int p,q,k,a,b;
 //    D();
         while(scanf("%d%d%d%d%d",&p,&q,&k,&a,&b)!=EOF){

    // long long m,n;
 //    while(cin>>m>>n)///C(m,n)
 //    {
        // cout<<C[m][n]<<endl;
 //    }
 //int c = (int)C(m,n);
 //int l = (int)pow(p,b);
 //int f = (int)pow(q,n);
 //prlong longf("%lld",(long long)pow(p,b));
 printf("%lld\n",ll(pow64(p, a) * pow64(q, b) % MOD * C(k, a) % MOD));
    // return 0;
 }
 }