一文读懂PID控制算法（抛弃公式，从原理上真正理解PID控制）

 

PID控制应该算是应用非常广泛的控制算法了。小到控制一个元件的温度，大到控制无人机的飞行姿态和飞行速度等等，都可以使用PID控制。这里我们从原理上来理解PID控制。
PID(proportion integration differentiation)其实就是指比例，积分，微分控制。先把图片和公式摆出来，看不懂没关系。（一开始看这个算法，公式能看懂，具体怎么用怎么写代码也知道，但是就是不知道原理，不知道为什么要用比例，微分，积分这3个项才能实现最好的控制，用其中两个为什么不行，用了3个项能好在哪里，每一个项各有什么作用）

 

 

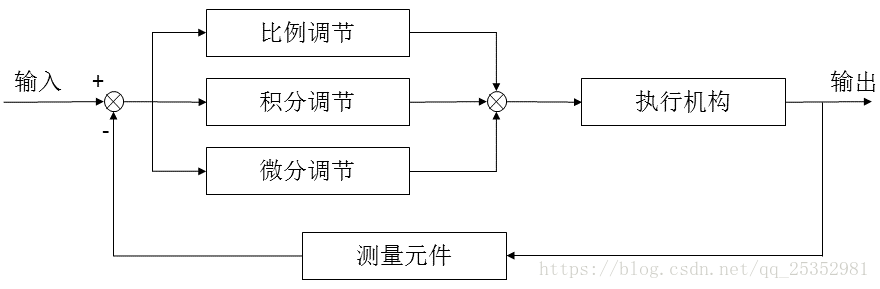
总的来说，当得到系统的输出后，将输出经过比例，积分，微分3种运算方式，叠加到输入中，从而控制系统的行为，下面用一个简单的实例来说明。

 

比例控制算法

我们先说PID中最简单的比例控制，抛开其他两个不谈。还是用一个经典的例子吧。假设我有一个水缸，最终的控制目的是要保证水缸里的水位永远的维持在1米的高度。假设初试时刻，水缸里的水位是0.2米，那么当前时刻的水位和目标水位之间是存在一个误差的error，且error为0.8.这个时候，假设旁边站着一个人，这个人通过往缸里加水的方式来控制水位。如果单纯的用比例控制算法，就是指加入的水量u和误差error是成正比的。即
u=kp*error
假设kp取0.5，
那么t=1时（表示第1次加水，也就是第一次对系统施加控制），那么u=0.5*0.8=0.4，所以这一次加入的水量会使水位在0.2的基础上上升0.4，达到0.6.
接着，t=2时刻（第2次施加控制），当前水位是0.6，所以error是0.4。u=0.5*0.4=0.2，会使水位再次上升0.2，达到0.8.
如此这么循环下去，就是比例控制算法的运行方法。
可以看到，最终水位会达到我们需要的1米。
但是，单单的比例控制存在着一些不足，其中一点就是 –稳态误差！（我也是看了很多，并且想了好久才想通什么是稳态误差以及为什么有稳态误差）。
像上述的例子，根据kp取值不同，系统最后都会达到1米，不会有稳态误差。但是，考虑另外一种情况，假设这个水缸在加水的过程中，存在漏水的情况，假设每次加水的过程，都会漏掉0.1米高度的水。仍然假设kp取0.5，那么会存在着某种情况，假设经过几次加水，水缸中的水位到0.8时，水位将不会再变换！！！因为，水位为0.8，则误差error=0.2.  所以每次往水缸中加水的量为u=0.5*0.2=0.1.同时，每次加水缸里又会流出去0.1米的水！！！加入的水和流出的水相抵消，水位将不再变化！！
也就是说，我的目标是1米，但是最后系统达到0.8米的水位就不在变化了，且系统已经达到稳定。由此产生的误差就是稳态误差了。
（在实际情况中，这种类似水缸漏水的情况往往更加常见，比如控制汽车运动，摩擦阻力就相当于是“漏水”，控制机械臂、无人机的飞行，各类阻力和消耗都可以理解为本例中的“漏水”）
所以，单独的比例控制，在很多时候并不能满足要求。

积分控制算法

还是用上面的例子，如果仅仅用比例，可以发现存在暂态误差，最后的水位就卡在0.8了。于是，在控制中，我们再引入一个分量，该分量和误差的积分是正比关系。所以，比例+积分控制算法为：
u=kp*error+ ki∗∫∗∫error
还是用上面的例子来说明，第一次的误差error是0.8，第二次的误差是0.4，至此，误差的积分（离散情况下积分其实就是做累加），∫∫error=0.8+0.4=1.2.   这个时候的控制量，除了比例的那一部分，还有一部分就是一个系数ki乘以这个积分项。由于这个积分项会将前面若干次的误差进行累计，所以可以很好的消除稳态误差（假设在仅有比例项的情况下，系统卡在稳态误差了，即上例中的0.8，由于加入了积分项的存在，会让输入增大，从而使得水缸的水位可以大于0.8，渐渐到达目标的1.0.）这就是积分项的作用。

 

微分控制算法

换一个另外的例子，考虑刹车情况。平稳的驾驶车辆，当发现前面有红灯时，为了使得行车平稳，基本上提前几十米就放松油门并踩刹车了。当车辆离停车线非常近的时候，则使劲踩刹车，使车辆停下来。整个过程可以看做一个加入微分的控制策略。
微分，说白了在离散情况下，就是error的差值，就是t时刻和t-1时刻error的差，即u=kd*（error（t）-error（t-1）），其中的kd是一个系数项。可以看到，在刹车过程中，因为error是越来越小的，所以这个微分控制项一定是负数，在控制中加入一个负数项，他存在的作用就是为了防止汽车由于刹车不及时而闯过了线。从常识上可以理解，越是靠近停车线，越是应该注意踩刹车，不能让车过线，所以这个微分项的作用，就可以理解为刹车，当车离停车线很近并且车速还很快时，这个微分项的绝对值（实际上是一个负数）就会很大，从而表示应该用力踩刹车才能让车停下来。
切换到上面给水缸加水的例子，就是当发现水缸里的水快要接近1的时候，加入微分项，可以防止给水缸里的水加到超过1米的高度，说白了就是减少控制过程中的震荡。

现在在回头看这个公式，就很清楚了

 

 

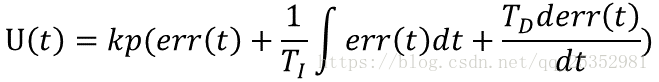
括号内第一项是比例项，第二项是积分项，第三项是微分项，前面仅仅是一个系数。很多情况下，仅仅需要在离散的时候使用，则控制可以化为
 
 

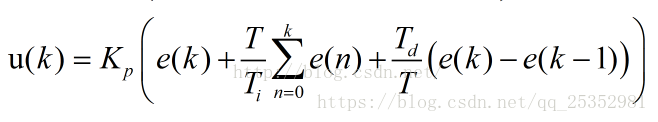
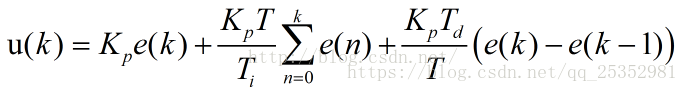
每一项前面都有系数，这些系数都是需要实验中去尝试然后确定的，为了方便起见，将这些系数进行统一一下：
 

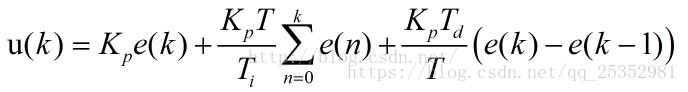
这样看就清晰很多了，且比例，微分，积分每个项前面都有一个系数，且离散化的公式，很适合编程实现。
讲到这里，PID的原理和方法就说完了，剩下的就是实践了。在真正的工程实践中，最难的是如果确定三个项的系数，这就需要大量的实验以及经验来决定了。通过不断的尝试和正确的思考，就能选取合适的系数，实现优良的控制器。
————————————————
版权声明：本文为CSDN博主「确定有穷自动机」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/qq_25352981/article/details/81007075