[CSP-S模拟测试]:蛇（DP+构造+哈希）

题目传送门（内部题140）

---

输入格式

　　前两行有两个长度相同的字符串，描述林先森花园上的字母。
　　第三行一个字符串$S$。

---

输出格式

　　输出一行一个整数，表示有多少种可能的蛇，对$10^9+7$取模。

---

样例

样例输入1：

rwby
ybwr
rwby

样例输出1：

4

样例输入2：

ooo
ooo
oo

样例输出2：

14

---

数据范围与提示

　　对于$20\%$的数据，$n,|S|\leqslant 16$。
　　对于$40\%$的数据，$n,|S|\leqslant 40$。
　　对于$60\%$的数据，$n,|S|\leqslant 200$。
　　对于$100\%$的数据，$1\leqslant n,|S|\leqslant 2,000$，输入中只包含小写字母。

---

题解

先来考虑路径蛇的路径，可以将其拆解成如下图中的三部分$\downarrow$

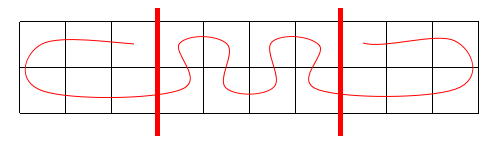
蛇一定是先向一个方向走$a$格，再回来；然后乱走（扭动着），然后再向另一个方向走$b$格，再回来。

一样不一样可以用哈希判断。

然后考虑$DP$，定义$dp[i]][j][k]$表示到了点$(i,j)$，匹配到了$k$的方案数。

避免出现环可以外层循环$k$。

为了方便，可以先默认向一个方向走；然后再把整张图翻转再跑一遍就好了。

注意蛇的长度为$1$和$2$的情况下需要特判。

时间复杂度：$\Theta(|S|^2)$。

期望得分：$100$分。

实际得分：$100$分。

---

代码时刻

#include<bits/stdc++.h>
using namespace std;
const int mod=1000000007;
struct rec{int s,x,y;};
int a[2][2001],b[2001],n,s;
char ch[2001];
long long dp[2][2001][4001][2],ans;
unsigned long long hsh[2001],flag[2001]={1},has[2][2][2002];
unsigned long long ask(bool x,bool y,int l,int r){return y?has[x][y][r]-has[x][y][l+1]*flag[l-r+1]:has[x][y][r]-has[x][y][l-1]*flag[r-l+1];}
unsigned long long get(int l,int r){return hsh[r]-hsh[l-1]*flag[r-l+1];}
void work()
{
	for(int i=0;i<2;i++)
		for(int j=1;j<=n;j++)
			has[i][0][j]=has[i][0][j-1]*131+a[i][j];
	for(int i=0;i<2;i++)
		for(int j=n;j;j--)
			has[i][1][j]=has[i][1][j+1]*131+a[i][j];
	for(int i=0;i<2;i++)
		for(int j=1;j<=n;j++)
		{
			dp[i][j][1][0]=(a[i][j]==b[1]);
			for(int k=2;k<=j;k++)
				dp[i][j][k<<1][1]=(ask(i^1,1,j,j-k+1)==get(1,k))&&(ask(i,0,j-k+1,j)==get(k+1,k<<1));
		}
	for(int k=1;k<=s;k++)
		for(int i=0;i<2;i++)
			for(int j=1;j<=n;j++)
			{
				if(a[i][j]!=b[k])continue;
				dp[i][j][k][0]=(dp[i][j][k][0]+dp[i][j-1][k-1][0]+dp[i][j-1][k-1][1])%mod;
				dp[i][j][k][1]=(dp[i][j][k][1]+dp[i^1][j][k-1][0])%mod;
			}
	for(int i=0;i<2;i++)
		for(int j=1;j<=n;j++)
			for(int k=0;k<=s;k++)
			{
				int res=(s-k)>>1;
				if(!((s-k)&1)&&res!=1&&(s==k||(j+res<=n&&ask(i,0,j+1,j+res)==get(k+1,k+res)&&ask(i^1,1,j+res,j+1)==get(s-res+1,s))))
					ans=(ans+dp[i][j][k][0]+dp[i][j][k][1])%mod;
			}
}
int main()
{
	scanf("%s",ch+1);n=strlen(ch+1);
	for(int i=1;i<=n;i++)a[0][i]=ch[i]-'a'+1;
	scanf("%s",ch+1);
	for(int i=1;i<=n;i++)a[1][i]=ch[i]-'a'+1;
	scanf("%s",ch+1);s=strlen(ch+1);
	for(int i=1;i<=s;i++)
	{
		b[i]=ch[i]-'a'+1;
		flag[i]=flag[i-1]*131;
		hsh[i]=hsh[i-1]*131+b[i];
	}
	work();
	reverse(a[0]+1,a[0]+n+1);
	reverse(a[1]+1,a[1]+n+1);
	memset(dp,0,sizeof(dp));
	work();
	if(s==1)
	{
		for(int i=0;i<2;i++)
			for(int j=1;j<=n;j++)
				ans-=(a[i][j]==b[1]);
	}
	if(s==2)
	{
		for(int i=0;i<2;i++)
			for(int j=1;j<=n;j++)
				ans-=(a[i][j]==b[1]&&a[i^1][j]==b[2]);
	}
	printf("%lld",ans);
	return 0;
}

---

rp++