POJ 1410 Intersection (计算几何)

题目链接：POJ 1410

Description

You are to write a program that has to decide whether a given line segment intersects a given rectangle.

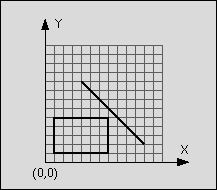
An example:

line: start point: (4,9)

end point: (11,2)

rectangle: left-top: (1,5)

right-bottom: (7,1)

Figure 1: Line segment does not intersect rectangle

The line is said to intersect the rectangle if the line and the rectangle have at least one point in common. The rectangle consists of four straight lines and the area in between. Although all input values are integer numbers, valid intersection points do not have to lay on the integer grid.

Input

The input consists of n test cases. The first line of the input file contains the number n. Each following line contains one test case of the format:

xstart ystart xend yend xleft ytop xright ybottom

where (xstart, ystart) is the start and (xend, yend) the end point of the line and (xleft, ytop) the top left and (xright, ybottom) the bottom right corner of the rectangle. The eight numbers are separated by a blank. The terms top left and bottom right do not imply any ordering of coordinates.

Output

For each test case in the input file, the output file should contain a line consisting either of the letter "T" if the line segment intersects the rectangle or the letter "F" if the line segment does not intersect the rectangle.

Sample Input

1
4 9 11 2 1 5 7 1

Sample Output

F

Source

Southwestern European Regional Contest 1995

Solution

题意

给定一个矩形和一条线段，判断线段是否与矩形相交或者在矩形内部。

思路

判断线段是否与矩形每条边相交。至于线段是否在矩形内，判断是否线段两个端点在矩形内即可。

计算几何模板来在 kuangbin 的模板。

Code

#include <cstdio>
#include <iostream>
#include <vector>
#include <cmath>
#include <algorithm>
using namespace std;
typedef long long ll;
typedef double db;
const db eps = 1e-10;
const db pi = acos(-1.0);
const ll inf = 0x3f3f3f3f3f3f3f3f;
const ll maxn = 1e5 + 10;

inline int sgn(db x) {
    if(fabs(x) < eps) return 0;
    return x > 0? 1: -1;
}

class Point {
public:
    double x, y;
    Point(double x = 0, double y = 0) : x(x), y(y) {}
    void input() {
        scanf("%lf%lf", &x, &y);
    }
    bool operator ==(Point b) const {
		return sgn(x-b.x) == 0 && sgn(y-b.y) == 0;
	}
    Point operator -(const Point &b) const {
		return Point(x - b.x, y - b.y);
	}
    //叉积
	double operator ^(const Point &b) const {
		return x*b.y - y*b.x;
	}
	//点积
	double operator *(const Point &b) const {
		return x*b.x + y*b.y;
	}
};

class Line {
public:
    Point s, e;
    db angle;
    Line() {}
    Line(Point s, Point e) : s(s), e(e) {}
    inline void input() {
        scanf("%lf%lf%lf%lf", &s.x, &s.y, &e.x, &e.y);
    }
    //`两线段相交判断`
	//`2 规范相交`
	//`1 非规范相交`
	//`0 不相交`
	int segcrossseg(Line v){
		int d1 = sgn((e - s) ^ (v.s - s));
		int d2 = sgn((e - s) ^ (v.e - s));
		int d3 = sgn((v.e - v.s) ^ (s - v.s));
		int d4 = sgn((v.e - v.s) ^ (e - v.s));
		if( (d1 ^ d2) == -2 && (d3 ^ d4) == -2 ) return 2;
		return (d1 == 0 && sgn((v.s - s)*(v.s - e)) <= 0) ||
			    (d2 == 0 && sgn((v.e - s)*(v.e - e)) <= 0) ||
			    (d3 == 0 && sgn((s - v.s) * (s - v.e)) <= 0) ||
			    (d4 == 0 && sgn((e - v.s) * (e - v.e)) <= 0);
	}
    // 点在线段上的判断
	bool pointonseg(Point p) {
		return sgn((p - s) ^ (e - s)) == 0 && sgn((p - s) * (p - e)) <= 0;
	}
};

struct Rec {
    const static int n = 4;
    Point p[4];
    Line l[4];
    void getline(){
		for(int i = 0; i < n; ++i) {
			l[i] = Line(p[i], p[(i + 1) % n]);
		}
	}
    //`判断点和任意多边形的关系`
    //` 3 点上`
    //` 2 边上`
    //` 1 内部`
    //` 0 外部`
    int relationpoint(Point q) {
        for(int i = 0; i < n; ++i) {
            if(p[i] == q) return 3;
        }
        getline();
        for(int i = 0; i < n; ++i) {
            if(l[i].pointonseg(q)) return 2;
        }
        int cnt = 0;
        for(int i = 0; i < n; ++i) {
            int j = (i + 1) % n;
            int k = sgn((q - p[j])^(p[i] - p[j]));
            int u = sgn(p[i].y - q.y);
            int v = sgn(p[j].y - q.y);
            if(k > 0 && u < 0 && v >= 0) cnt++;
            if(k < 0 && v < 0 && u >= 0) cnt--;
        }
        return cnt != 0;
    }
};

int main() {
    int T;
    scanf("%d", &T);
    while(T--) {
        Point a, b;
        a.input(), b.input();
        Line l = Line(a, b);
        Rec rec;
        a.input(), b.input();
        rec.p[0] = Point(min(a.x, b.x), min(a.y, b.y));
        rec.p[1] = Point(max(a.x, b.x), min(a.y, b.y));
        rec.p[2] = Point(max(a.x, b.x), max(a.y, b.y));
        rec.p[3] = Point(min(a.x, b.x), max(a.y, b.y));
        if(l.segcrossseg(Line(rec.p[0], rec.p[1]))) {
            printf("T\n");
            continue;
        }
        if(l.segcrossseg(Line(rec.p[1], rec.p[2]))) {
            printf("T\n");
            continue;
        }
        if(l.segcrossseg(Line(rec.p[2], rec.p[3]))) {
            printf("T\n");
            continue;
        }
        if(l.segcrossseg(Line(rec.p[3], rec.p[0]))) {
            printf("T\n");
            continue;
        }
        if(rec.relationpoint(l.s) || rec.relationpoint(l.e)) {
            printf("T\n");
            continue;
        }
        printf("F\n");
    }
    return 0;
}