分享某Python下的mpi教程 —— A Python Introduction to Parallel Programming with MPI 1.0.2 documentation

如题：

无意中发现了一个Python下的mpi教程《A Python Introduction to Parallel Programming with MPI 1.0.2 documentation》

地址如下：

https://materials.jeremybejarano.com/MPIwithPython/#

=================================================================

这里给出自己的一些学习笔记：

Point-to-Point Communication

The Trapezoidal Rule

关于这个梯形规则，推荐资料：

https://wenku.baidu.com/view/20a29f97dd88d0d233d46a48.html

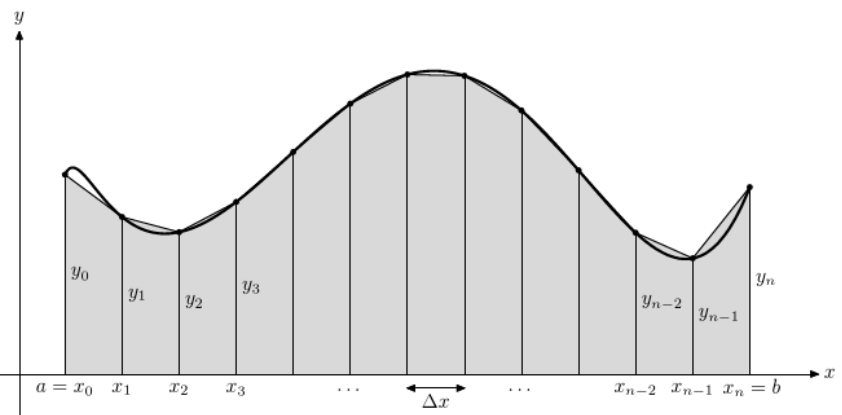
这个梯形规则就是将一个函数的积分形式用一个近似的采样计算的方法来进行求解。

也就有了原文中的公式：

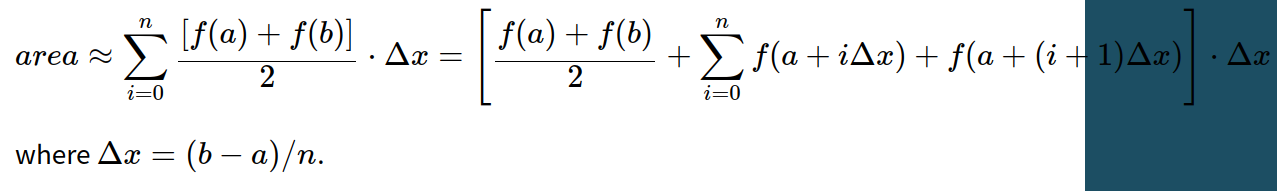
不过原文中的公式不是很好看懂，还是百度文库的那个文档讲解的比较好：

https://wenku.baidu.com/view/20a29f97dd88d0d233d46a48.html

原文中的代码，修改后：

# trapSerial.py
# example to run: python trapSerial.py 0.0 1.0 10000

import numpy
import sys
import time

# takes in command-line arguments [a,b,n]
a = float(sys.argv[1])
b = float(sys.argv[2])
n = int(sys.argv[3])

def f(x):
    return x * x

def integrateRange(a, b, n):
    '''Numerically integrate with the trapezoid rule on the interval from
        a to b with n trapezoids.
        '''
    integral = -(f(a) + f(b)) / 2.0

    # n+1 endpoints, but n trapazoids
    #for x in numpy.linspace(a, b, n + 1):
    #    integral = integral + f(x)
    integral = integral + numpy.sum( f(numpy.linspace(a, b, n + 1)) )

    integral = integral * (b - a) / n
    return integral

begin_time = time.time()
integral = integrateRange(a, b, n)
end_time = time.time()

print("With n =", n, "trapezoids, our estimate of the integral\
from", a, "to", b, "is", integral)

print("total run time :", end_time - begin_time)

该代码为单机代码，在原始代码基础上改进为向量计算，进一步提高运算的效率。

改进后的mpi代码：

# trapParallel_1.py
# example to run: mpiexec -n 4 python trapParallel_1.py 0.0 1.0 10000
import numpy
import sys
import time
from mpi4py import MPI
from mpi4py.MPI import ANY_SOURCE

comm = MPI.COMM_WORLD
rank = comm.Get_rank()
size = comm.Get_size()

# takes in command-line arguments [a,b,n]
a = float(sys.argv[1])
b = float(sys.argv[2])
n = int(sys.argv[3])

# we arbitrarily define a function to integrate
def f(x):
    return x * x

# this is the serial version of the trapezoidal rule
# parallelization occurs by dividing the range among processes
def integrateRange(a, b, n):
    integral = -(f(a) + f(b)) / 2.0
    # n+1 endpoints, but n trapazoids
    # for x in numpy.linspace(a, b, n + 1):
    #    integral = integral + f(x)
    integral = integral + numpy.sum(f(numpy.linspace(a, b, n + 1)))
    integral = integral * (b - a) / n
    return integral

# local_n is the number of trapezoids each process will calculate
# note that size must divide n
local_n = int(n / size)
# h is the step size. n is the total number of trapezoids
h = (b - a) / (local_n*size)

# we calculate the interval that each process handles
# local_a is the starting point and local_b is the endpoint
local_a = a + rank * local_n * h
local_b = local_a + local_n * h

# initializing variables. mpi4py requires that we pass numpy objects.
recv_buffer = numpy.zeros(size)

if rank == 0:
    begin_time = time.time()
# perform local computation. Each process integrates its own interval
integral = integrateRange(local_a, local_b, local_n)

# communication
# root node receives results from all processes and sums them
if rank == 0:
    recv_buffer[0] = integral
    for i in range(1, size):
        comm.Recv(recv_buffer[i:i+1], ANY_SOURCE)
    total = numpy.sum(recv_buffer)
else:
    # all other process send their result
    comm.Send(integral, dest=0)

# root process prints results
if comm.rank == 0:
    end_time = time.time()
    print("With n =", n, "trapezoids, our estimate of the integral from" \
          , a, "to", b, "is", total)
    print("total run time :", end_time - begin_time)
    print("total size: ", size)

运行命令：

mpiexec -np 4  python  trapSerial_1.py  0 1000000 100000000

上面改进的代码本身也实现了原文中所提到的计算负载均衡的问题，不过上面的改进方法是通过修改总的切分个数，从而实现总的切分个数可以被运行进数所整除。

假设我们总共要切分的数量为1099，但是我们要进行计算的进程数量为100，那么每个进程需要分配多少切分数来进行计算呢，下面给出另一种改进方式，在改变总切分数量的前提下使每个进程所负责计算的切分数均为平均。

改进代码：

# trapParallel_2.py
# example to run: mpiexec -n 4 python trapParallel_1.py 0.0 1.0 10000
import numpy
import sys
import time
from mpi4py import MPI
from mpi4py.MPI import ANY_SOURCE

comm = MPI.COMM_WORLD
rank = comm.Get_rank()
size = comm.Get_size()

# takes in command-line arguments [a,b,n]
a = float(sys.argv[1])
b = float(sys.argv[2])
n = int(sys.argv[3])

# we arbitrarily define a function to integrate
def f(x):
    return x * x

# this is the serial version of the trapezoidal rule
# parallelization occurs by dividing the range among processes
def integrateRange(a, b, n):
    integral = -(f(a) + f(b)) / 2.0
    # n+1 endpoints, but n trapazoids
    # for x in numpy.linspace(a, b, n + 1):
    #    integral = integral + f(x)
    integral = integral + numpy.sum(f(numpy.linspace(a, b, n + 1)))
    integral = integral * (b - a) / n
    return integral

# h is the step size. n is the total number of trapezoids
h = (b - a) / n
# local_n is the number of trapezoids each process will calculate
# note that size must divide n
local_n = numpy.zeros(size, dtype=numpy.int32)
local_n[:] = n // size
if n%size!=0:
    local_n[-(n%size):] += 1

# we calculate the interval that each process handles
# local_a is the starting point and local_b is the endpoint
local_a = numpy.sum(local_n[:rank]) * h
local_b = local_a + local_n[rank] * h

# initializing variables. mpi4py requires that we pass numpy objects.
recv_buffer = numpy.zeros(size)

if rank == 0:
    begin_time = time.time()
# perform local computation. Each process integrates its own interval
integral = integrateRange(local_a, local_b, local_n[rank])

# communication
# root node receives results from all processes and sums them
if rank == 0:
    recv_buffer[0] = integral
    for i in range(1, size):
        comm.Recv(recv_buffer[i:i+1], ANY_SOURCE)
    total = numpy.sum(recv_buffer)
else:
    # all other process send their result
    comm.Send(integral, dest=0)

# root process prints results
if comm.rank == 0:
    end_time = time.time()
    print("With n =", n, "trapezoids, our estimate of the integral from" \
          , a, "to", b, "is", total)
    print("total run time :", end_time - begin_time)
    print("total size: ", size)

计算负载均衡的核心代码为：

# h is the step size. n is the total number of trapezoids
h = (b - a) / n
# local_n is the number of trapezoids each process will calculate
# note that size must divide n
local_n = numpy.zeros(size, dtype=numpy.int32)
local_n[:] = n // size
if n%size!=0:
    local_n[-(n%size):] += 1

# we calculate the interval that each process handles
# local_a is the starting point and local_b is the endpoint
local_a = numpy.sum(local_n[:rank]) * h
local_b = local_a + local_n[rank] * h

运行命令：

mpiexec      --oversubscribe      -np 100       python   trapSerial_2.py    0     1000000       1099

最后的改进方法更好的实现了计算的负载均衡。

==================================================

上面的改进方法对应集体通信的话又该如何改进呢？？？

Collective Communication

The Parallel Trapezoidal Rule 2.0

改进方法1对应的 trapParallel_1.py   改进：

# trapParallel_1.py
# example to run: mpiexec -n 4 python26 trapParallel_2.py 0.0 1.0 10000
import numpy
import sys
import time
from mpi4py import MPI
from mpi4py.MPI import ANY_SOURCE

comm = MPI.COMM_WORLD
rank = comm.Get_rank()
size = comm.Get_size()

# takes in command-line arguments [a,b,n]
a = float(sys.argv[1])
b = float(sys.argv[2])
n = int(sys.argv[3])

# we arbitrarily define a function to integrate
def f(x):
    return x * x

# this is the serial version of the trapezoidal rule
# parallelization occurs by dividing the range among processes
def integrateRange(a, b, n):
    integral = -(f(a) + f(b)) / 2.0
    # n+1 endpoints, but n trapazoids
    #for x in numpy.linspace(a, b, n + 1):
    #    integral = integral + f(x)
    integral = integral + numpy.sum(f(numpy.linspace(a, b, n + 1)))
    integral = integral * (b - a) / n
    return integral

# local_n is the number of trapezoids each process will calculate
# note that size must divide n
local_n = int(n / size)
# h is the step size. n is the total number of trapezoids
h = (b - a) / (local_n*size)

# we calculate the interval that each process handles
# local_a is the starting point and local_b is the endpoint
local_a = a + rank * local_n * h
local_b = local_a + local_n * h

# initializing variables. mpi4py requires that we pass numpy objects.
#integral = numpy.zeros(1)
total = numpy.zeros(1)

if rank == 0:
    begin_time = time.time()
# perform local computation. Each process integrates its own interval
integral = integrateRange(local_a, local_b, local_n)

# communication
# root node receives results with a collective "reduce"
comm.Reduce(integral, total, op=MPI.SUM, root=0)

# root process prints results
if comm.rank == 0:
    end_time = time.time()
    print("With n =", n, "trapezoids, our estimate of the integral from" \
          , a, "to", b, "is", total)
    print("total run time :", end_time - begin_time)
    print("total size: ", size)

运行命令：

mpiexec  --oversubscribe -np 100   python    trapSerial_1.py     0    1000000    1099

改进方法2 对应的 trapParallel_2.py   改进：

# trapParallel_2.py
# example to run: mpiexec -n 4 python26 trapParallel_2.py 0.0 1.0 10000
import numpy
import sys
import time
from mpi4py import MPI
from mpi4py.MPI import ANY_SOURCE

comm = MPI.COMM_WORLD
rank = comm.Get_rank()
size = comm.Get_size()

# takes in command-line arguments [a,b,n]
a = float(sys.argv[1])
b = float(sys.argv[2])
n = int(sys.argv[3])

# we arbitrarily define a function to integrate
def f(x):
    return x * x

# this is the serial version of the trapezoidal rule
# parallelization occurs by dividing the range among processes
def integrateRange(a, b, n):
    integral = -(f(a) + f(b)) / 2.0
    # n+1 endpoints, but n trapazoids
    #for x in numpy.linspace(a, b, n + 1):
    #    integral = integral + f(x)
    integral = integral + numpy.sum(f(numpy.linspace(a, b, n + 1)))
    integral = integral * (b - a) / n
    return integral

# h is the step size. n is the total number of trapezoids
h = (b - a) / n
# local_n is the number of trapezoids each process will calculate
# note that size must divide n
local_n = numpy.zeros(size, dtype=numpy.int32)
local_n[:] = n // size
if n%size!=0:
    local_n[-(n%size):] += 1

# we calculate the interval that each process handles
# local_a is the starting point and local_b is the endpoint
local_a = numpy.sum(local_n[:rank]) * h
local_b = local_a + local_n[rank] * h

# initializing variables. mpi4py requires that we pass numpy objects.
#integral = numpy.zeros(1)
total = numpy.zeros(1)

if rank == 0:
    begin_time = time.time()
# perform local computation. Each process integrates its own interval
integral = integrateRange(local_a, local_b, local_n[rank])

# communication
# root node receives results with a collective "reduce"
comm.Reduce(integral, total, op=MPI.SUM, root=0)

# root process prints results
if comm.rank == 0:
    end_time = time.time()
    print("With n =", n, "trapezoids, our estimate of the integral from" \
          , a, "to", b, "is", total)
    print("total run time :", end_time - begin_time)
    print("total size: ", size)

运行命令：

mpiexec  --oversubscribe -np 100   python    trapSerial_2.py     0    1000000    1099

====================================================