Codeforces Round #739 (Div. 3) 个人题解（A~F2）

比赛链接：Here

1560A. Dislike of Threes

Description

找出第 $k$ 大的不可被 $3$ 整除以及非 $3$ 结尾的整数

直接枚举出前 1000 个符合条件的数，然后输出

int main() {

    cin.tie(nullptr)->sync_with_stdio(false);

    vector<int>a;

    int i = 1;

    while (a.size() != 1000) {

        if (i % 3 != 0 && i % 10 != 3) a.push_back(i);

        i += 1;

    }

    int _; for (cin >> _; _--;) {

        int n; cin >> n;

        cout << a[n - 1] << "\n";

    }

}

1560B. Who's Opposite?

Description

一些人均匀站成一圈，每人的编号从 $1$ 开始，给定 $a,b,c$ 三个整数，$a,b$ 是通过圆心看向对方，请问是否存在 $c$ 的对位，如果存在则输出相应编号，否则输出 $-1$

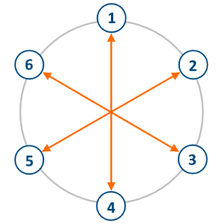
通过样图容易发现对位的编号差的两倍即 $n$ 的大小，所以如果 $c$ 存在对位的话，肯定是 $c + Siz / 2\ or\ c - Siz/2$

当然注意边界

int main() {

    cin.tie(nullptr)->sync_with_stdio(false);

    int _; for (cin >> _; _--;) {

        int a, b, c; cin >> a >> b >> c;

        int n = 2 * abs(a - b);

        if (a > n || b > n || c > n) {cout << "-1\n"; continue;}

        cout << (n / 2 + c - 1) % n + 1 << "\n";

    }

}

1560C. Infinity Table

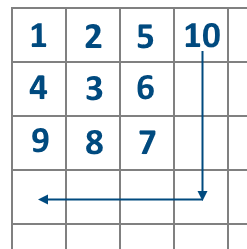
题意：给定 $n$ 请问 $n$ 在第几行第几列

好明显的规律题？但赛时没想太多，跑了暴力

先找到第 $i$ 行第 $i$ 列的数值，然后在第 $i$ 行和第 $i$ 列上循环跑一下即可
因为 $n\le 10^9$ 最多 $10^3$ 行保证不会 TLE

void solve() {

    ll x; cin >> x;

    ll i = 1;

    while (i * i < x) i++;

    ll j = i - 1;

    ll tmp = x - j * j;

    if (tmp <= i) cout << tmp << " " << i << endl;

    else {

        int t = i * i - x;

        cout << i << " " << t + 1 << endl;

    }

}

1560D. Make a Power of Two

D题开始搞自己了，

给定一个整数 $n (n\le 10^9)$ 和两种操作，

删除 $n$ 的任何一位
在最右边加一位（可以是 $0\sim 9$ 任何一个数）

请问最少的操作数使得 $n$ 为 $2^k(0\le k)$

\[QAQ
\]

这很明显 $k$ 最大也就 $64$ ，直接枚举了，然后比较原字符串和 $2^k$ 的位数差：$len_s +len_t - 2 * cnt$ ，$cnt$ 为相同位数个数

相同类型：AcWing 3796. 凑平方

来自群友的详细思路，From 群友d3ac

题目关键信息: 随便删除,只能在右边加,前导零不自动删除

因为要看看到底操作几次就可以变得和$2^k\ \ (0\le k\le 63)$相等,拿到题我们就先想暴力一点的做法,判断时间复杂度,再考虑优化.所以最暴力的就是直接枚举$2^k$,再与$n$来作比较,看看需要操作几次

计算时间复杂度:$10^4*63*9$<$10^{8-9}$,所以行.

然后再来考虑怎么把$n$与$2^k$进行比较,来计算需要几个操作,这个其实就是字符串匹配,将$2^k$来匹配原来的$n$,因为只能从左边添加字符,假设$2^k=1024$所以$n$中必须是有从$1$到$4$连续且有顺序排列的才行,举个例子:$n=1052$,匹配成功了$3$个,$n=2052$,匹配成功$0$个,因为必须要删除完所有的才能加入$1$.

再考虑一点小小的优化和怎么写才好写
将$2^k$预处理出来,放在一个数组里面方便每次用,减少时间复杂度.

将$n$和$2^k$都转换为字符串,方便处理.

设$n$的字符串下长度为$Len$,匹配成功了$now$个(注意,$now$指向的是下一个位置,所以要$now--$),当前$2^k$的长度是$len[i]$.最终的答案就是$len[i]-now+Len-now$,其中$len[i]-now$是$n$需要添加的,$Len-now$是需要删除的.

注意:需要枚举到$2^{32}$才行

int main() {

    cin.tie(nullptr)->sync_with_stdio(false);

    int _; for (cin >> _; _--;) {

        string s; cin >> s;

        int ans = 1e9;

        for (int i = 0; i < 64; ++i) {

            string t = to_string(1ull << i);

            int k = 0;

            for (int j = 0; j < int(s.size()); ++j)

                if (k < int(t.size()) && s[j] == t[k]) k += 1;

            ans = min(ans, int(s.size() + int(t.size()) - 2 * k));

        }

        cout << ans << '\n';

    }

}

1560E. Polycarp and String Transformation

From 群友d3ac

首先思考一下给出的字符串那么长,到底该怎么去分割开,要是分割开,那就爽歪歪.

以$everywherevrywhrvryhrvrhrvhv$为例子

正常分割$everywhere \ \ vrywhr \ \ vryhr \ \ vrhr \ \ vh \ \ v$

所以不难看到,要想把他分出来还是有点难度的,但是每次会删除一个字符,我们再倒过来看看,先是只有一种字母,然后再是只有两种字符……有全部的字母,所以我们倒序枚举,从字符串的末尾开始向头开始枚举的话,就可以找到删除的顺序,因为后删除的字符肯定在后面还会出现的,而先删除的字符就只会在前面,会后被枚举到,因此,我们找到了删除的顺序

再来考虑原字符串是什么,先这样,我们统计一下每个字母在大字符串出现了多少次,结果是这样的:

$e=4$,$w=2$,$y=3$,$r=8$,$h=5$,$v=6$.

每个字符在每次轮回的时候出现次数都是一样的,在删除了它之前是一个特定值$x$,删除后就是$0$,所以我们将所有的字符出现次数除上它是第几个被删除掉的,结果就是这样了

$e=4$,$w=1$,$y=1$,$r=2$,$h=1$,$v=1$

然而母串,也就是原字符串中,每个字母出现次数也是也么多次.

至此,我们已经求出了字符串和顺序,要考虑$-1$就简单了,就是模拟题目所说过程,用我们得到的字符串去看,行不行就好了

注意:要memset 反例:aaabbb

int main() {

    cin.tie(nullptr)->sync_with_stdio(false);

    int _; for (cin >> _; _--;) {

        string t; cin >> t;

        reverse(t.begin(), t.end());

        map<char, int> freq;

        string ord;

        for (char c : t) {

            if (!freq[c]) ord += c;

            freq[c] += 1;

        }

        int n = int(ord.length());

        int len = 0;

        for (int i = 0; i < n; ++i) len += freq[ord[i]] / (n - i);

        reverse(t.begin(), t.end());

        if (len > t.size()) {

            cout << "-1\n";

            continue;

        }

        string s = t.substr(0, len);

        reverse(ord.begin(), ord.end());

        string reals = s;

        string fin = "";

        for (char c : ord) {

            fin += s;

            string news ;

            for (char d : s)

                if (d != c) news += d;

            s = news;

        }

        if (fin == t) cout << reals << " " << ord << "\n";

        else cout << "-1\n";

    }

}

1560F2. Nearest Beautiful Number (hard version)

翻译一下官方题解（官方题解解释的很清楚，好评）

假设数字 $n$ 包含 $m$ 位数字，其十进制表示为 $d_1d_2…d_m$。所需的数字 $x$ 不大于由 $m$ 个数字 9 组成的数字。这个数字是 1-beautiful，而任何 1-beautiful 数字同时是 k-beautiful，所以 $x$ 最多包含 $m$ 个数字。同时，$x≥n$ 所以 $x$ 至少包含 $m$ 位数字。因此，所需的数字正好包含 $m$ 位数字。

因为我们要寻找最小的 $x$，所以我们需要首先最小化第一个数字，然后再最小化第二个数字，等等。因此，我们需要找到 $n$ 的十进制表示的前缀，它是十进制表示的前缀的 $x$。让我们贪心地做吧。

我们找出包含不超过 $k$ 个不同数字的 $n$ 的最大前缀。假设前缀的长度为 $p$。如果 $p=m$，那么 $n$ 已经是 k-beautiful 的了，直接输出即可。否则，让我们像数字一样将前缀增加 $1$，例如如果 $n=1294$ 且 $p=3$，那么我们将 $129$ 加 $1$，结果前缀为 $130$。所有其他数字 $(d_{p+2},d_{p+3},...,d_m)$，让我们设置为零（例如，如果 $n=1294$ 并且 $p=3$，那么 $n$ 就会变成 $1300$ ）。旧 $n$ 的答案就是新 $n$ 的答案。为了得到新 $n$ 的答案，让我们再次开始描述的过程来准备新 $n$。

具体可以再参考代码理解

时间复杂度：$\mathcal{O}(m^2)$

void solve() {

    string s;

    int k;

    cin >> s >> k;

    while (true) {

        set<char> cs;

        for (auto c : s) cs.insert(c);

        if (cs.size() <= k) {cout << s << "\n"; return ;}

        cs.clear();

        int lst = 0;

        for (;; lst++) {

            cs.insert(s[lst]);

            if (cs.size() > k) {

                while (s[lst] == '9') lst -= 1;

                s[lst]++;

                for (int i = lst + 1; i < s.size(); ++i) s[i] = '0';

                break;

            }

        }

    }

}

JLY 关于F1的代码：Here