A* 算法、PathFinding问题中的 allow diagonal 和 don't cross corners，以及 .map文件格式（续）

前文：

A* 算法、PathFinding问题中的 allow diagonal 和 don't cross corners，以及 .map文件格式

上篇讲了些关于地图文件 .map 的介绍，本文主要讲下PathFindding中的allow diagonal 和 don't cross corners。

---

---

在PathFinding问题中每个点都是一个坐标点，在地图中大致形式如下：

但是在实际地图显示中是不会以点的显示来形式的，地图上每一个坐标点都是用一个小方块来进行表示的，一个完整的地图（带有坐标点的形式）如下：

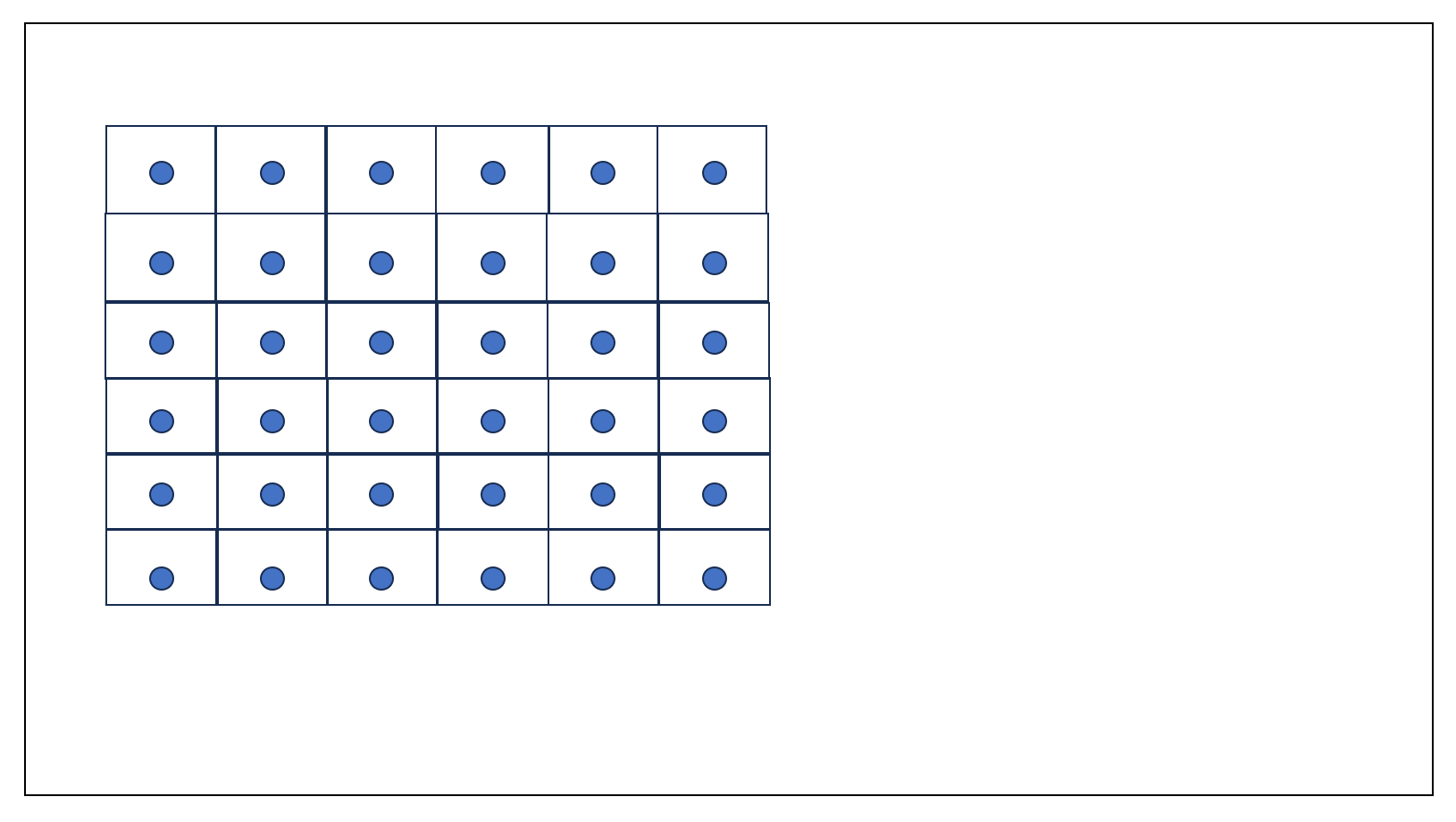
也就是说每个坐标点是(x, y)的形式，但是在图形显示的时候是使用一个方块的形式，在实际计算的时候我们依然使用坐标点(x, y)的形式，方块只是用于可视化形式，一个坐标点和其具体的显示形式如下：

关于 allow diagonal ：

顾名思义，这个选项代表是否可以用对角线的形式连接坐标点，下面给出一个不使用对角线连接的一个路径图示意：

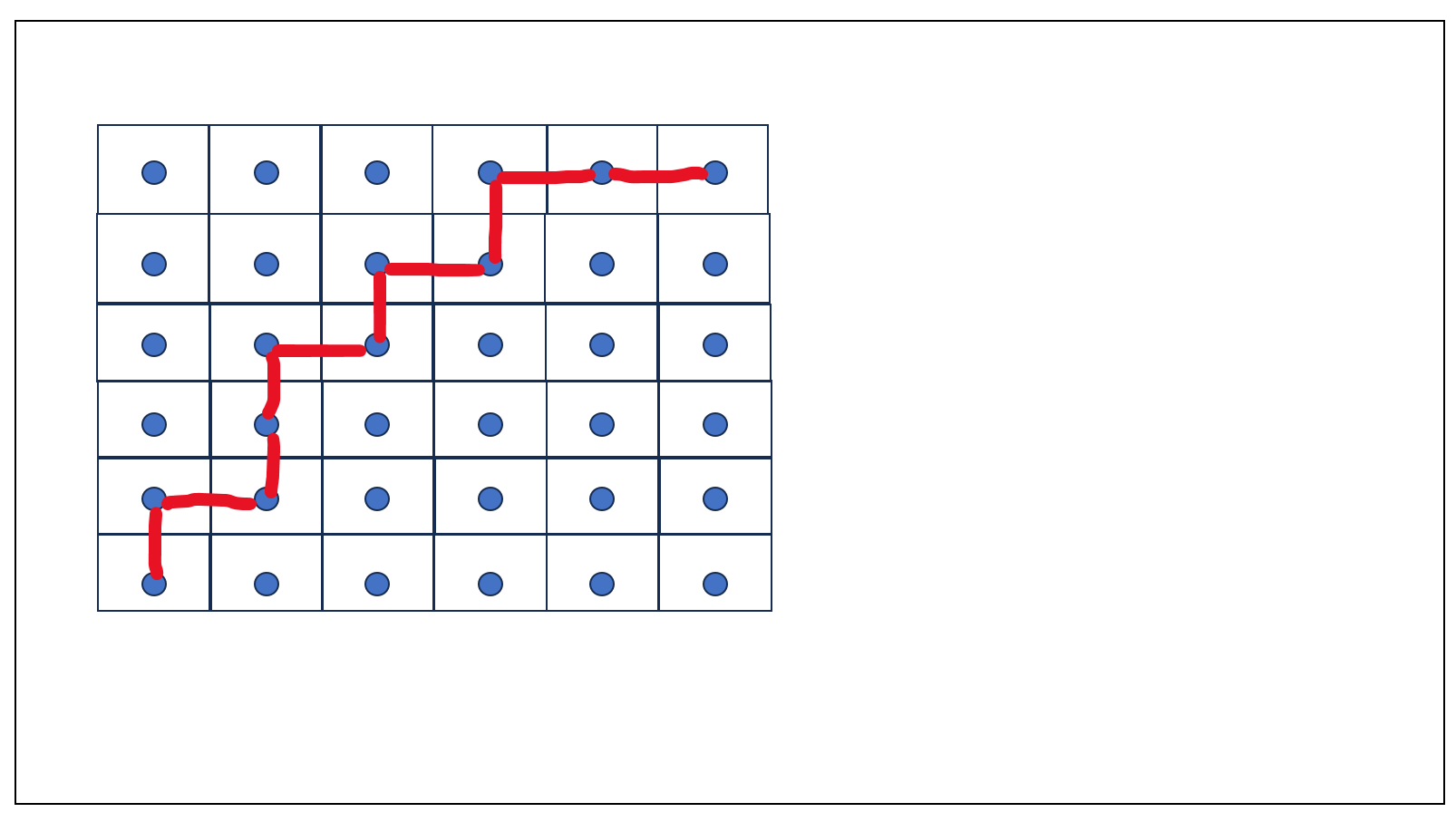
可以看到坐标点之间的连接都是横向和纵向的，没有对角线方向的。

如果使用对角线连接的方式，示意图如下：

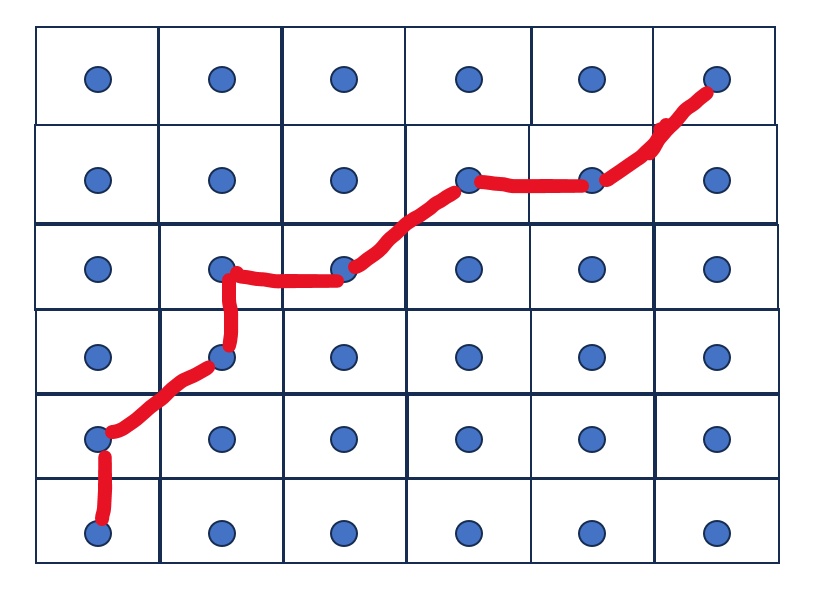
重点在于下面的这个对角结构：

假设坐标点之间的间距为1，那么方块的长宽也为1，如果不允许对角线连接的情况下坐标点之间的连接长度只能为1，但是如果允许对角线连接那么相邻坐标点之间的连接距离可以为1也可以为\(\sqrt{2}\)

关于don't cross corners ：

在论文：https://webdocs.cs.ualberta.ca/~nathanst/papers/benchmarks.pdf

中可以知道，在允许对角线连接的情况下（ allow diagonal ），如果don't cross corners对角线两侧的坐标均不能被占用（不能有障碍物，必须是可穿越的）

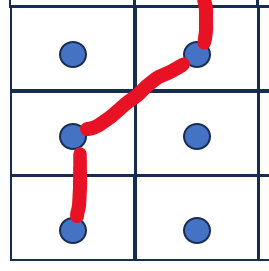
下面这个对角线是可以穿越的（allow diagonal 并且 don't cross corners）：

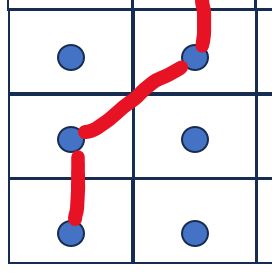
但是，如果对角线两侧有障碍物则不能对角线连接，如：

（下面三种形式在allow diagonal 并且 don't cross corners情况下是违法的，是不允许存在的）

(1)

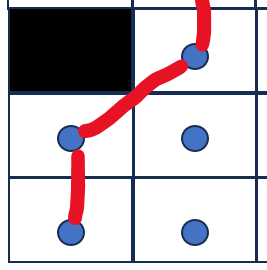
(2)

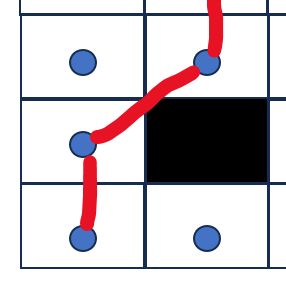
(3)（这种情况不论是否 allow diagonal 也不论是否 don't cross corners 均是违法的）

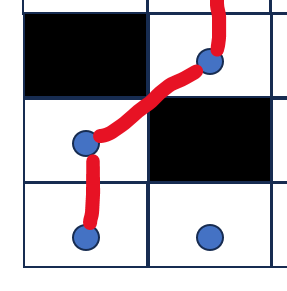
也就是说在don't cross corners情况下，即使allow diagonal，那么在上面的三种情况不能进行对角线连接。

在don't cross corners情况下，如果allow diagonal，那么上面的三种情况只能像下面这样处理：

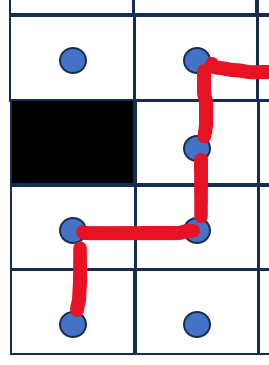
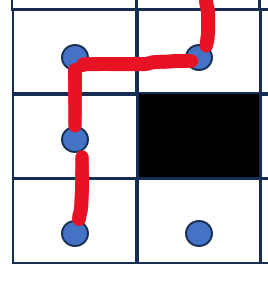
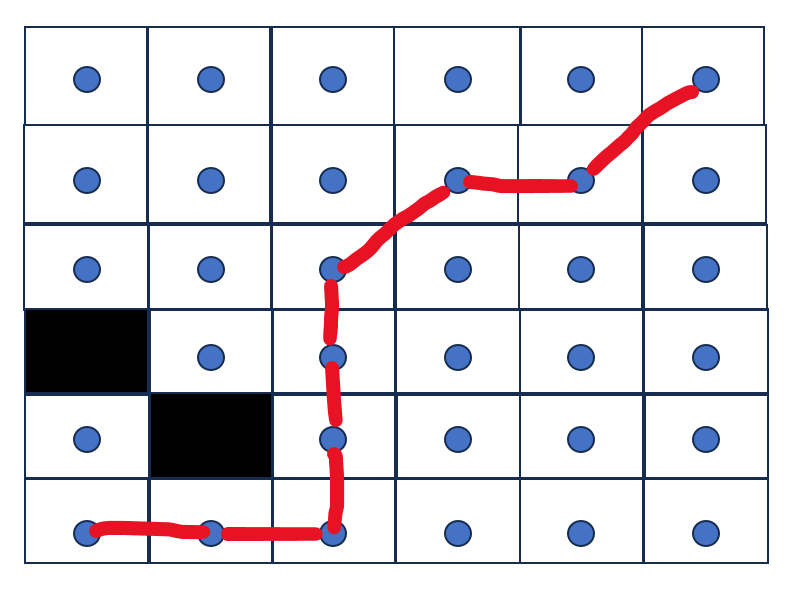
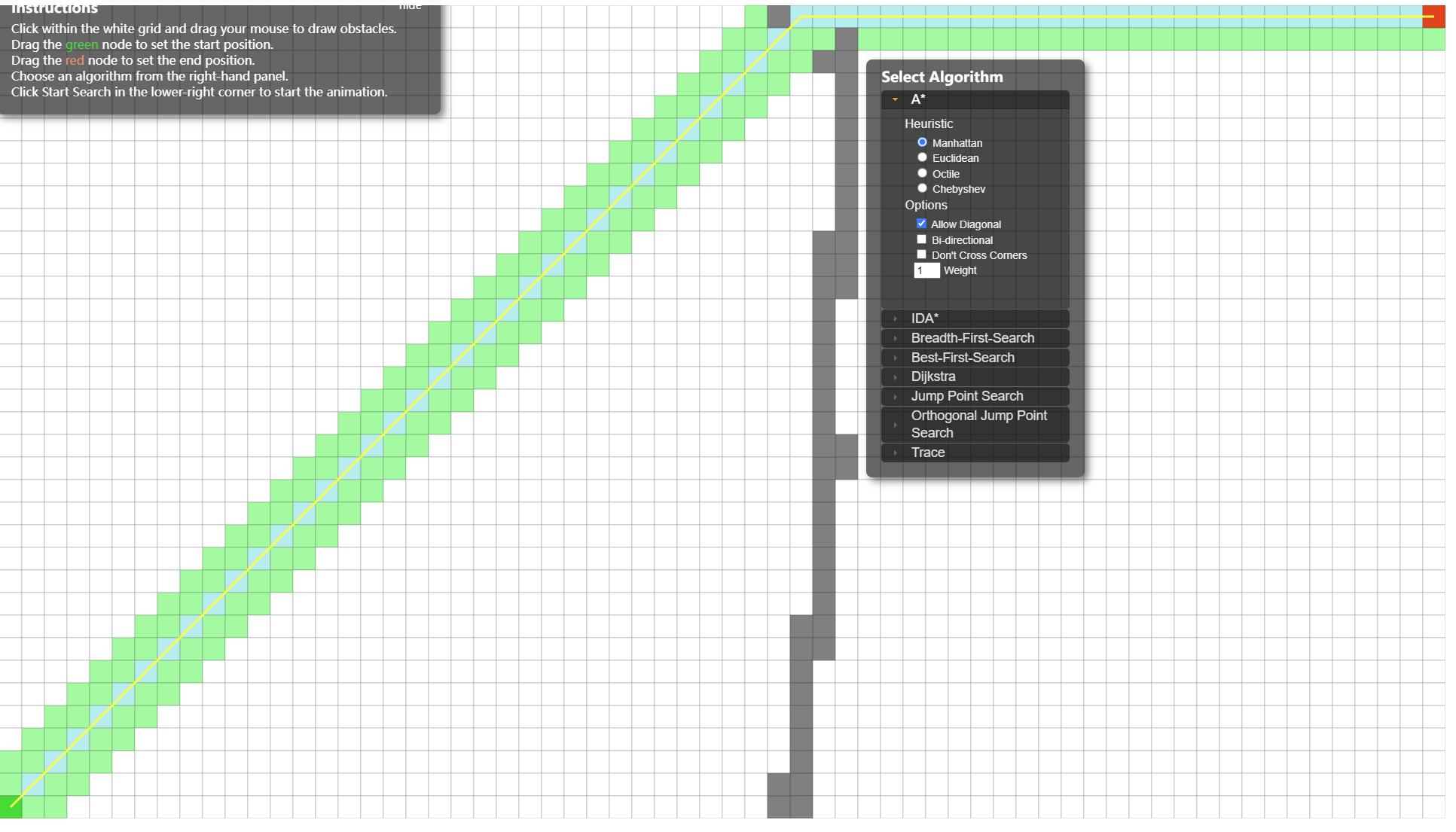
为了更形象的说明在don't cross corners情况下，allow diagonal是不能在相邻坐标点的连接对角线两侧有不可穿越点的，给出下面的App应用的演示：

App地址：https://qiao.github.io/PathFinding.js/visual/

例子：(允许cross corners)

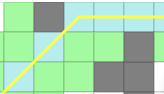
重点在：

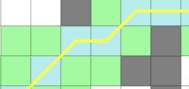
上面的情况，如果 allow diagonal 并且 don't cross corners，则有：