2023 版 Java和python开发线性代数探索

目录

• 前景提示
• 需求
• 分析
  • 1、初始化不需要指定矩阵的尺寸，并且可以直接传入数据。
  • 2、可以计算2x2矩阵的逆
  • 3、可以做2x2的矩阵乘法
• Java版本开发
  • 一、 开发详情
    • 1、开发一个子类，如图所示。
    • 2、根据问题修改子类，父类，以便真实可用
      • 解决1、初始化不需要指定矩阵的尺寸，并且可以直接传入数据。
      • 解决 2、可以计算2x2矩阵的逆
      • （1） 第二题第一问，全为零打印
      • （2）第二题第二问，逆矩阵输出
      • 解决 3、可以做2x2的矩阵乘法
      • （1） 第三题第一问，逆矩阵乘法
      • （2）第三题第二问，复合乘法
  • 二、最终完整版
  • 三、其他相关方法的测试
• Python版本开发
  • 一、python代码
    • 1、导入 包
    • 2、创建数组
    • 3、打印数组
    • 4、求矩阵的逆
    • 5、矩阵的乘法
    • 6、完整版
    • 7、测试结果
    • 8、拓展其他功能

前景提示

• 最近小伙伴问了一个题目，就是用Java开发线性代数，本身Java的能力并不是很擅长做这样的工作，需要计算的话还是用python开发更好，方便快捷，简单方便，但是，既然有这样的需求还是需要进行开发的，毕竟没有客户会管你多么费劲，只会说你开发不了水平不够，这边进行了九个小时的开发，开发了Java和python两个版本，本文的优势就在于系统全面，并且拿来可用，对于那些急于解决问题，完成作业的小伙伴，非常友好，因此，这篇文章对你帮助极大，希望你喜欢。

需求

• 题目如下如这样。

分析

1、初始化不需要指定矩阵的尺寸，并且可以直接传入数据。

• 题目一的要求翻译一下，就是要(1)写一个子类继承父类，(2)子类要有一个构造方法可以传入double[]类型的数据，（3）打印的结果要像图例那样，所以要重写showInfo方法（这是没重写实际运行发现的，初期没觉得要重写）

2、可以计算2x2矩阵的逆

• 题目翻译：(1) 要开发一个get_inverse()在子类中（2）要增加一个判断判断在矩阵中全是0的时候要有判断输出。

3、可以做2x2的矩阵乘法

• 题目翻译：(1) 要开发一个方法mul(m3)，可以做矩阵的乘法 （2）方法之间可以互相调用mul().showInfo().

Java版本开发

一、 开发详情

1、开发一个子类，如图所示。

---

父类

package com.grandfather.www.marixs;

/**
 * @projectName: marixs
 * @package: com.grandfathers.www.marixs
 * @className: BaseMatrix
 * @author: your-father
 * @description: TODO
 * @date: 2023-09-30 20:58
 * @version: 1.0
 */
public class BaseMatrix {

    // 矩阵的行列数
    int m = 0, n = 0;

    // 矩阵的数据
    float data[];

    public BaseMatrix() {
    }

    // 构造函数
    public BaseMatrix(int m, int n) {
        this.m = m;
        this.n = n;
        this.data = new float[m * n];
    }

    // 设置矩阵
    public void setData(float[] data) {
        this.data = data;
    }

    public float[] getData() {
        return data;
    }

    // 显示矩阵的信息
    void showInfo() {

        System.out.println("-----------");

        System.out.println("矩阵尺寸为: " + m + "x" + n);

        System.out.println("矩阵的数据为 : ");

        for (int i = 0; i < this.data.length; i++) {

            System.out.println(this.data[i] + ",");

            if ((i + 1) % n == 0) {
                System.out.println("\n");
            }
        }

        System.out.println("------------");

    }

    // 矩阵加法
    BaseMatrix add(BaseMatrix m2) {

        if ((this.m == m2.m) && (this.n == m2.n)) {

            float[] d = new float[m * n];

            for (int i = 0; i < m * n; i++) {
                d[i] = this.data[i] + m2.data[i];
            }

            BaseMatrix baseMatrix = new BaseMatrix(m, n);

            // 结果放到新的矩阵中
            baseMatrix.setData(d);

            return baseMatrix;
        } else {

            System.out.println("两个矩阵尺寸不一致,无法做加法");

            return null;
        }

    }

}

子类

public class Marix_2X2 extends BaseMatrix {

    public static void main(String[] args) {

        // 查看矩阵
        Marix_2X2 marix2X2 = new Marix_2X2();
        marix2X2.setData(new float[]{1, 2, 2, 5});
        marix2X2.n=2;
        marix2X2.showInfo();

    }

}

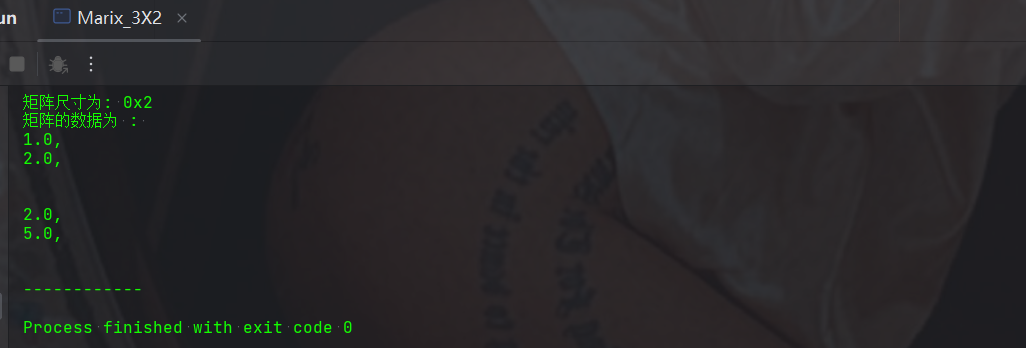
• 建个基础的版本，可以做个继承BaseMatrix，查看其父类的方法，什么也不改就只能像上面这样使用，可以看到，跟测试完全不一样，打印的结果中间有个大空格，这样不符合题目的要求，因此，需要改造。

2、根据问题修改子类，父类，以便真实可用

解决1、初始化不需要指定矩阵的尺寸，并且可以直接传入数据。

• 首先要在子类里添加构造方法

  public class Marix_2X2 extends BaseMatrix {

    public Marix_2X2() {
    }

    public Marix_2X2(float[] data) {
        super();
        this.data = data;
        createBase(data);
    }

    BaseMatrix createBase(float[] data) {

        int m = 0, n = 0;

        for (int i = 0; i < data.length; i++) {

            if (i % 2 == 0) {
                n = i;
            } else {
                m = i;
            }

        }

        this.m = m;
        this.n = n;

        BaseMatrix baseMatrix = new BaseMatrix(m, n);

        // 结果放到新的矩阵中
        baseMatrix.setData(data);

        return baseMatrix;
    }

}

• 其次要重写showInfo() 方法

  // 显示矩阵的信息
      @Override
      void showInfo() {
  
          System.out.println("-----------");
  
          System.out.println("矩阵尺寸为: " + (m - 1) + "x" + n);
  
          System.out.println("矩阵的数据为 : ");
  
          for (int i = 0; i < this.data.length; i++) {
  
              System.out.print(this.data[i] + ",");
  
              if ((i + 1) % n == 0) {
                  System.out.println();
              }
          }
  
          System.out.println("------------");
          System.out.println();
  
      }
  
  

• 最终第一个版本结果。（题目一的要求就满足了）

  package com.grandfather.www.marixs;
  
  /**
   * @projectName: marixs
   * @package: com.grandfathers.www.marixs
   * @className: Marix_2X2
   * @author: your-father
   * @description: TODO
   * @date: 2023-09-30 21:14
   * @version: 1.0
   */
  public class Marix_2X2 extends BaseMatrix {
  
      public Marix_2X2() {
      }
  
      public Marix_2X2(float[] data) {
          super();
          this.data = data;
          createBase(data);
      }
  
      BaseMatrix createBase(float[] data) {
  
          int m = 0, n = 0;
  
          for (int i = 0; i < data.length; i++) {
  
              if (i % 2 == 0) {
                  n = i;
              } else {
                  m = i;
              }
  
          }
  
          this.m = m;
          this.n = n;
  
          BaseMatrix baseMatrix = new BaseMatrix(m, n);
  
          // 结果放到新的矩阵中
          baseMatrix.setData(data);
  
          return baseMatrix;
      }
  
      // 显示矩阵的信息
      @Override
      void showInfo() {
  
          System.out.println("-----------");
  
          System.out.println("矩阵尺寸为: " + (m - 1) + "x" + n);
  
          System.out.println("矩阵的数据为 : ");
  
          for (int i = 0; i < this.data.length; i++) {
  
              System.out.print(this.data[i] + ",");
  
              if ((i + 1) % n == 0) {
                  System.out.println();
              }
          }
  
          System.out.println("------------");
          System.out.println();
  
      }
  
      public static void main(String[] args) {
  
          // 查看矩阵
          Marix_2X2 marix2X2 = new Marix_2X2(new float[]{1, 2, 2, 5});
          marix2X2.showInfo();
  
      }
  }
  
  

  

解决 2、可以计算2x2矩阵的逆

• 这里就写的比较复杂了，主要是一般都是按照二维数组的处理方式处理的，而题目给的书传入一个一维数组，所以这里总是要处理，一维数组变二维，二维数组变一维这样的问题。

样例一

 // 判断数组的元素是否全为0
 boolean flag = true;

 private Marix_2X2 get_inverse() {

        Marix_2X2 m1 = new Marix_2X2(this.data);

        if (null != this.data) {

            float[] newdata = this.data;

            int temp = 0;

            for (int i = 0; i < newdata.length; i++) {
                if (newdata[i] == 0) {
                    temp++;
                }
            }

            if (temp == newdata.length) {
                m1.flag = false;
            } else {

                float[][] newdata2 = new float[this.m - 1][this.n];
                newdata2 = one2Two(newdata, newdata2);

                float[][] floats = gaussianElimination(newdata2);

                float[] result = two2One(floats, newdata);

                m1.setData(result);

                return m1;
            }

            return m1;
        } else {

            System.out.println("为传入合法的数据....");

            return null;
        }
    }

    float[][] gaussianElimination(float[][] arr) {
        int i, j, k;

        float tem_1, tem_2, tem_3;
        int N = arr.length;
        float[][] W = new float[N][2 * N];
        float[][] result = new float[N][N];

        // 对矩阵右半部分进行扩增
        for (i = 0; i < arr.length; i++) {
            for (j = 0; j < 2 * arr.length; j++) {
                if (j < arr.length) {
                    W[i][j] = arr[i][j];
                } else {
                    W[i][j] = (float) (j - N == i ? 1 : 0);
                }
            }
        }

        for (i = 0; i < N; i++) {
            // 判断矩阵第一行第一列的元素是否为0，若为0，继续判断第二行第一列元素，直到不为0，将其加到第一行
            if (((int) W[i][i]) == 0) {
                for (j = i + 1; j < N; j++) {
                    if (((int) W[j][i]) != 0) {
                        break;
                    }
                }
                if (j == N) {
                    System.out.print("这个矩阵不能求逆");
                    break;
                }
                //将前面为0的行加上后面某一行
                for (k = 0; k < 2 * N; k++) {
                    W[i][k] += W[j][k];
                }
            }

            //将前面行首位元素置1
            tem_1 = W[i][i];
            for (j = 0; j < 2 * N; j++) {
                W[i][j] = W[i][j] / tem_1;
            }

            //将后面所有行首位元素置为0
            for (j = i + 1; j < N; j++) {
                tem_2 = W[j][i];
                for (k = i; k < 2 * N; k++) {
                    W[j][k] = W[j][k] - tem_2 * W[i][k];
                }
            }
        }

        // 将矩阵前半部分标准化
        for (i = N - 1; i >= 0; i--) {
            for (j = i - 1; j >= 0; j--) {
                tem_3 = W[j][i];
                for (k = i; k < 2 * N; k++) {
                    W[j][k] = W[j][k] - tem_3 * W[i][k];
                }
            }
        }

        //得出逆矩阵
        for (i = 0; i < N; i++) {
            for (j = N; j < 2 * N; j++) {
                result[i][j - N] = W[i][j];
            }
        }

        return result;

    }

    /*！！！注意：
     * 1.传入的数组里两个数组的大小（一维数组length为10，则二维数组的行数乘列数也为10
     * 2.数组类型必须一样
     * */
    public static float[][] one2Two(float[] data, float[][] da) {
        int k = 0;
        int hang = da.length;
        int lie = 0;

        if (!isAllZero(da)) {
            lie = da[0].length;
        } else {
            lie = 1;
        }

        for (int i = 0; i < hang; i++) {
            for (int j = 0; j < lie; j++) {
                da[i][j] = data[k];
                k++;
            }
        }

        return da;
    }

    /*！！！注意：
     * 1.传入的数组里两个数组的大小（一维数组length为10，则二维数组的行数乘列数也为10
     * 2.数组类型必须一样
     * */
    public static float[] two2One(float[][] da, float[] data) {
        int k = 0;
        int hang = da.length;
        int lie = 0;
        if (!isAllZero(da)) {
            lie = da[0].length;
        } else {
            lie = 1;
        }

        for (int i = 0; i < hang; i++) {
            for (int j = 0; j < lie; j++) {
                data[k] = da[i][j];
                k++;
            }
        }

        return data;
    }

    private static boolean isAllZero(float[][] onwResult) {
        int temp = 0;

        for (float[] floats : onwResult) {
            for (float aFloat : floats) {
                if (aFloat == 0) {
                    temp++;
                }
            }
        }

        if (temp == onwResult.length) {
            return true;
        } else {
            return false;
        }
    }

    // 添加了全为0 的判断
    // 显示矩阵的信息
    @Override
    void showInfo() {

        if (flag) {
            System.out.println("-----------");

            System.out.println("矩阵尺寸为: " + (m - 1) + "x" + n);

            System.out.println("矩阵的数据为 : ");

            for (int i = 0; i < this.data.length; i++) {

                System.out.print(this.data[i] + ",");

                if ((i + 1) % n == 0) {
                    System.out.println();
                }
            }

            System.out.println("------------");
            System.out.println();
        } else {
            System.out.println("行列式为0,不能求逆矩阵");
            System.out.println();
        }

    }

测试

       // 全为0的矩阵
        Marix_2X2 m1 = new Marix_2X2(new float[]{0, 0, 0, 0});
        Marix_2X2 tmp = m1.get_inverse();
        assert tmp != null;
        tmp.showInfo();

（1） 第二题第一问，全为零打印

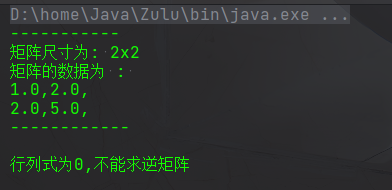
（2）第二题第二问，逆矩阵输出

解决 3、可以做2x2的矩阵乘法

• 矩阵乘法也没有什么问题，但是这里发现第一个结果跟题目的答案不一样，因此，经过反复debug发现是上个逆矩阵的算法有问题，因此这里又修改了逆矩阵的算法，最终，结果一致了。

• 错误的输出

  

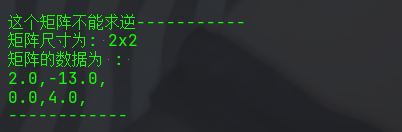
矩阵的乘法

private Marix_2X2 mul(Marix_2X2 m3) {

        float[][] a = new float[this.m - 1][this.n];
        one2Two(this.getData(), a);

        float[][] b = new float[this.m - 1][this.n];
        one2Two(m3.getData(), b);

        float[][] c = new float[this.m - 1][this.n];
        float[] newdata = this.data;

        for (int i = 0; i < a.length; i++) {
            for (int j = 0; j < a.length; j++) {
                for (int k = 0; k < a.length; k++) {
                    c[i][j] += a[i][k] * b[k][j];
                }
            }
        }

        float[] result = two2One(c, newdata);

        m3.setData(result);

        return m3;
    }

替换逆矩阵算法

    //求解逆矩阵
    public Marix_2X2 get_inverse_2() {

        Marix_2X2 m1 = new Marix_2X2(this.data);

        if (null != this.data) {

            int temp = 0;

            float[] onwResult = this.data;

            temp = isAllZero(temp, onwResult);

            if (temp == onwResult.length) {
                m1.flag = false;
            } else {

                float[][] floats = new float[this.m - 1][this.n];

                float[][] floats2 = one2Two(m1.getData(), floats);

                int row = floats2.length;
                float[][] floats1 = CopyArry(floats2);
                float[][] floats6 = new float[row][row];
                float[][] floats7 = AdjointMatrix(floats1);
                for (int i = 0; i < row; i++) {
                    for (int i1 = 0; i1 < row; i1++) {
                        floats6[i][i1] = floats7[i][i1] / ArrayCount(floats1, row);
                    }
                }

                float[] result = two2One(floats6, onwResult);

                m1.setData(result);

            }
            return m1;
        } else {

            System.out.println("为传入合法的数据....");

            return null;
        }
    }

    //矩阵的复制
    public static float[][] CopyArry(float[][] floats) {
        int row = floats.length;
        float[][] floats1 = new float[row][row];
        for (int i = 0; i < row; i++) {
            for (int i1 = 0; i1 < row; i1++) {
                floats1[i][i1] = floats[i][i1];
            }
        }
        return floats1;
    }

    //矩阵求伴随矩阵
    public static float[][] AdjointMatrix(float[][] floats) {

        int row = floats.length;
        float[][] floats1 = CopyArry(floats);

        float[][] floats4 = new float[row][row];
        for (int i = 0; i < row; i++) {
            for (int i1 = 0; i1 < row; i1++) {

                floats4[i1][i] = (-1) * (((i + i1) % 2) == 1 ? 1 : -1) * ArrayCount(RemoveRC(floats1, row, i, i1), row - 1);
            }
        }
        return floats4;
    }

    // 计算数组行列式方法
    public static float ArrayCount(float a[][], int n) {

        float p = 0;

        for (int k = 0; k <= n - 2; k++) {
            for (int r = k + 1; r <= n - 1; r++) {
                if (a[k][k] == 0) {
                    try {
                        ArrayChange(a, k, n);
                    } catch (Exception e) {
                        System.out.println(e.getMessage());
                        return 0;
                    }
                }
                p = -(a[r][k] / a[k][k]);
                for (int i = k; i <= n - 1; i++) {
                    a[r][i] = a[k][i] * p + a[r][i];
                }
            }

        }
        float result = 1;
        for (int i = 0; i <= n - 1; i++) {
            result *= a[i][i];

        }

        return result;
    }

    /**
     * @param a 传入的数组
     * @param k 出现问题的元素的行和列的坐标数值
     * @param n 数组的长度 ，虽然是从0 标开始，但是这里仍然使用n来计数
     */
    public static void ArrayChange(float a[][], int k, int n) {
        float b[] = new float[n - k];
        int c = k;
        for (int i = k + 1; i <= n - 1; i++) {
            if (a[i][k] != 0) {
                c = i;
            }
        }
        if (c == k) {
            throw new RuntimeException("高斯求解失败");
        }
        int w = 0;
        for (int i = k; i <= n - 1; i++) {
            b[w] = a[k][i];
            a[k][i] = a[c][i];
            a[c][i] = b[w];
            w++;
        }

    }

    //去掉固定的行和列的行列式
    public static float[][] RemoveRC(float[][] floats, int n, int p, int q) {
        float[][] floats1 = new float[n][n];
        float[][] floats2 = new float[n - 1][n - 1];
        ArrayList<Float> arrayList = new ArrayList<>((n - 1) * (n - 1));
        for (int i = 0; i <= n - 1; i++) {
            for (int i1 = 0; i1 <= n - 1; i1++) {
                floats1[i][i1] = floats[i][i1];
            }

        }
        for (int i = 0; i <= n - 1; i++) {
            for (int i1 = 0; i1 <= n - 1; i1++) {
                if (i == p || i1 == q) {

                } else {
                    arrayList.add(floats[i][i1]);

                }
            }

        }
        Object[] objects = arrayList.toArray();
        int index = 0;
        for (int i = 0; i < n - 1; i++) {
            for (int i1 = 0; i1 < n - 1; i1++) {
                floats2[i][i1] = (float) objects[index];
                index++;

            }

        }

        return floats2;
    }

（1） 第三题第一问，逆矩阵乘法

• 测试代码

         // 矩阵的乘法
          Marix_2X2 m2 = new Marix_2X2(new float[]{2, 5, 1, 3});
          Marix_2X2 m3 = new Marix_2X2(new float[]{4, -6, 2, 1});
          m2.get_inverse_2().mul(m3).showInfo();
  

（2）第三题第二问，复合乘法

• 测试代码

          // 矩阵的复合乘法
          Marix_2X2 m4 = new Marix_2X2(new float[]{1, 4, -1, 2});
          Marix_2X2 m5 = new Marix_2X2(new float[]{3, 1, 0, -1});
          Marix_2X2 m6 = new Marix_2X2(new float[]{2, 0, -1, 1});
          m4.get_inverse_2().mul(m5).mul(m6.get_inverse_2()).showInfo();
  

  

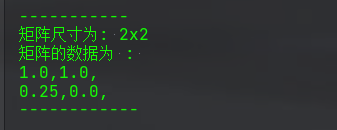
二、最终完整版

• 父类

package com.grandfathers.www.exersice;/**
 * @author: MrLiu
 * @createTime: 2023/09/30 20:58
 * @description: xxx
 */

/**
 * @projectName: anlysistSentence
 * @package: com.grandfathers.www.exersice
 * @className: BaseMatrix
 * @author: your-father
 * @description: TODO
 * @date: 2023-09-30 20:58
 * @version: 1.0
 */
public class BaseMatrix {

    // 矩阵的行列数
    int m = 0, n = 0;

    // 矩阵的数据
    float data[];

    public BaseMatrix() {
    }

    // 构造函数
    public BaseMatrix(int m, int n) {
        this.m = m;
        this.n = n;
        this.data = new float[m * n];
    }

//    public BaseMatrix(float[] data) {
//        this.data = data;
//        createBase(data);
//    }

    // 设置矩阵睡觉
    public void setData(float[] data) {
        this.data = data;
    }

    public float[] getData() {
        return data;
    }

    // 显示矩阵的信息
    void showInfo() {

        System.out.println("-----------");

        System.out.println("矩阵尺寸为: " + m + "x" + n);

        System.out.println("矩阵的数据为 : ");

        for (int i = 0; i < this.data.length; i++) {

            System.out.println(this.data[i] + ",");

            if ((i + 1) % n == 0) {
                System.out.println("\n");
            }
        }

        System.out.println("------------");

    }

    // 矩阵加法
    BaseMatrix add(BaseMatrix m2) {

        if ((this.m == m2.m) && (this.n == m2.n)) {

            float[] d = new float[m * n];

            for (int i = 0; i < m * n; i++) {
                d[i] = this.data[i] + m2.data[i];
            }

            BaseMatrix baseMatrix = new BaseMatrix(m, n);

            // 结果放到新的矩阵中
            baseMatrix.setData(d);

            return baseMatrix;
        } else {

            System.out.println("两个矩阵尺寸不一致,无法做加法");

            return null;
        }

    }

}

• 子类

  package com.grandfathers.www.exersice;/**
   * @author: MrLiu
   * @createTime: 2023/09/30 21:14
   * @description: xxx
   */
  
  import java.util.ArrayList;
  import java.util.Objects;
  
  import static java.lang.Math.pow;
  
  /**
   * @projectName: anlysistSentence
   * @package: com.grandfathers.www.exersice
   * @className: Marix_2X2
   * @author: your-father
   * @description: TODO
   * @date: 2023-09-30 21:14
   * @version: 1.0
   */
  public class Marix_2X2 extends BaseMatrix {
  
      // 判断数组的元素是否全为0
      boolean flag = true;
  
      public Marix_2X2(float[] data) {
          super();
          this.data = data;
          createBase(data);
      }
  
      BaseMatrix createBase(float[] data) {
  
          int m = 0, n = 0;
  
          for (int i = 0; i < data.length; i++) {
  
              if (i % 2 == 0) {
                  n = i;
              } else {
                  m = i;
              }
  
          }
  
          this.m = m;
          this.n = n;
  
          BaseMatrix baseMatrix = new BaseMatrix(m, n);
  
          // 结果放到新的矩阵中
          baseMatrix.setData(data);
  
          return baseMatrix;
      }
  
      // 显示矩阵的信息
      @Override
      void showInfo() {
  
          if (flag) {
              System.out.println("-----------");
  
              System.out.println("矩阵尺寸为: " + (m - 1) + "x" + n);
  
              System.out.println("矩阵的数据为 : ");
  
              for (int i = 0; i < this.data.length; i++) {
  
                  System.out.print(this.data[i] + ",");
  
                  if ((i + 1) % n == 0) {
                      System.out.println();
                  }
              }
  
              System.out.println("------------");
              System.out.println();
          } else {
              System.out.println("行列式为0,不能求逆矩阵");
              System.out.println();
          }
  
      }
  
      /**
       * <p>使用高斯消元法对矩阵进行求逆<p/>
       *
       * @param arr 二维矩阵
       * @return 矩阵的逆
       */
      float[][] gaussianElimination(float[][] arr) {
          int i, j, k;
  
          float tem_1, tem_2, tem_3;
          int N = arr.length;
          float[][] W = new float[N][2 * N];
          float[][] result = new float[N][N];
  
          // 对矩阵右半部分进行扩增
          for (i = 0; i < arr.length; i++) {
              for (j = 0; j < 2 * arr.length; j++) {
                  if (j < arr.length) {
                      W[i][j] = arr[i][j];
                  } else {
                      W[i][j] = (float) (j - N == i ? 1 : 0);
                  }
              }
          }
  
          for (i = 0; i < N; i++) {
              // 判断矩阵第一行第一列的元素是否为0，若为0，继续判断第二行第一列元素，直到不为0，将其加到第一行
              if (((int) W[i][i]) == 0) {
                  for (j = i + 1; j < N; j++) {
                      if (((int) W[j][i]) != 0) break;
                  }
                  if (j == N) {
                      System.out.print("这个矩阵不能求逆");
                      break;
                  }
                  //将前面为0的行加上后面某一行
                  for (k = 0; k < 2 * N; k++) {
                      W[i][k] += W[j][k];
                  }
              }
  
              //将前面行首位元素置1
              tem_1 = W[i][i];
              for (j = 0; j < 2 * N; j++) {
                  W[i][j] = W[i][j] / tem_1;
              }
  
              //将后面所有行首位元素置为0
              for (j = i + 1; j < N; j++) {
                  tem_2 = W[j][i];
                  for (k = i; k < 2 * N; k++) {
                      W[j][k] = W[j][k] - tem_2 * W[i][k];
                  }
              }
          }
  
          // 将矩阵前半部分标准化
          for (i = N - 1; i >= 0; i--) {
              for (j = i - 1; j >= 0; j--) {
                  tem_3 = W[j][i];
                  for (k = i; k < 2 * N; k++) {
                      W[j][k] = W[j][k] - tem_3 * W[i][k];
                  }
              }
          }
  
          //得出逆矩阵
          for (i = 0; i < N; i++) {
              for (j = N; j < 2 * N; j++) {
                  result[i][j - N] = W[i][j];
              }
          }
  
          return result;
  
      }
  
      /*！！！注意：
       * 1.传入的数组里两个数组的大小（一维数组length为10，则二维数组的行数乘列数也为10
       * 2.数组类型必须一样
       * */
      public static float[][] one2Two(float[] data, float[][] da) {
          int k = 0;
          int hang = da.length;
          int lie = 0;
  
          if (!isAllZero(da)) {
              lie = da[0].length;
          } else {
              lie = 1;
          }
  
          for (int i = 0; i < hang; i++) {
              for (int j = 0; j < lie; j++) {
                  da[i][j] = data[k];
                  k++;
              }
          }
  
          return da;
      }
  
      /*！！！注意：
       * 1.传入的数组里两个数组的大小（一维数组length为10，则二维数组的行数乘列数也为10
       * 2.数组类型必须一样
       * */
      public static float[] two2One(float[][] da, float[] data) {
          int k = 0;
          int hang = da.length;
          int lie = 0;
          if (!isAllZero(da)) {
              lie = da[0].length;
          } else {
              lie = 1;
          }
  
          for (int i = 0; i < hang; i++) {
              for (int j = 0; j < lie; j++) {
                  data[k] = da[i][j];
                  k++;
              }
          }
  
          return data;
      }
  
      private Marix_2X2 mul(Marix_2X2 m3) {
  
          float[][] a = new float[this.m - 1][this.n];
          one2Two(this.getData(), a);
  
          float[][] b = new float[this.m - 1][this.n];
          one2Two(m3.getData(), b);
  
          float[][] c = new float[this.m - 1][this.n];
          float[] newdata = this.data;
  
          for (int i = 0; i < a.length; i++) {
              for (int j = 0; j < a.length; j++) {
                  for (int k = 0; k < a.length; k++) {
                      c[i][j] += a[i][k] * b[k][j];
                  }
              }
          }
  
          float[] result = two2One(c, newdata);
  
          m3.setData(result);
  
          return m3;
      }
  
      //正交化
      public static float[][] Orthogonalization(float[][] floats) {
          float[][] floats1 = CopyArry(floats);
          int row = floats1.length;
  
          ArrayList<float[]> arrayList = new ArrayList<>();
          for (int i = 0; i < row; i++) {
              arrayList.add(i, new float[row]);
              for (int i1 = 0; i1 < row; i1++) {
                  arrayList.get(i)[i1] = floats1[i1][i];
              }
          }
  
          for (int i = 0; i < row; i++) {
              float[] floats2 = new float[row];
              CopySingleArray(arrayList.get(i), floats2);
              floats2 = XiuGindexN(floats1, i);
              CopySingleArray(floats1[i], floats2);
  
          }
  
          float[][] result = new float[row][row];
          for (int i = 0; i < row; i++) {
              for (int i1 = 0; i1 < row; i1++) {
                  result[i1][i] = floats1[i][i1];
              }
          }
          return result;
      }
  
      //定义单一数组的复制
  
      /**
       * @param floats1 即将要被修改的数组
       * @param floats2 参考数组
       *                修改了floats 1 数组
       */
      public static void CopySingleArray(float[] floats1, float[] floats2) {
          for (int i = 0; i < floats2.length; i++) {
              floats1[i] = floats2[i];
          }
      }
      //定义回溯积累的正交化中间方法
  
      /**
       * @param floats 传入的数组
       * @param index  数组的行数
       * @return 结果数组
       * 根据行数来求出第index个 正交化的行向量，
       */
      public static float[] XiuGindexN(float[][] floats, int index) {
          int row = floats.length;
          float[] result = new float[row];
          float[][] floats1 = CopyArry(floats);
          if (index == 0) {
              CopySingleArray(result, floats1[index]);
          } else {
              for (int i = index - 1; i >= 0; i--) {
                  float p = DeterminantProduct(floats1[index], floats1[i]) / DeterminantProduct(floats1[i], floats1[i]);
                  float[] floats2 = NumberTimesArray(-p, floats1[i]);
                  result = DeterminAntddition(result, floats2);
              }
              result = DeterminAntddition(result, floats1[index]);
          }
          return result;
      }
  
      //定义一个数和数组的乘法
      public static float[] NumberTimesArray(float f, float[] floats) {
          int row = floats.length;
          float[] floats1 = new float[row];
          for (int i = 0; i < row; i++) {
              floats1[i] = floats[i] * f;
          }
  
          return floats1;
      }
  
      //定义一个求两个数组积的方法
  
      /**
       * @param floats1 传入的第一个数组
       * @param floats2 传入的第二个数组
       * @return 返回一个结果，不对原有的参数地址内容进行修改，是一个可靠的方法
       */
      public static float DeterminantProduct(float[] floats1, float[] floats2) {
          float result = 0;
          int row = floats1.length;
          for (int i = 0; i < row; i++) {
              result += floats1[i] * floats2[i];
          }
  
          return result;
      }
  
      //定义正交基本矩阵计算
      public float[][] OrthogonalBasic(float[][] floats) {
          int row = floats.length;
          float[][] floats1 = getData(new Marix_2X2(this.getData()).Transpose());
  
          return Orthogonalization(floats1);
  
      }
  
      //定义正交基本单位化计算
      public static float[][] OrthogonalasicUnit(float[][] floats) {
          int row = floats.length;
          float[][] floats1 = CopyArry(floats);
          return Unitization(new Marix_2X2(two2One(floats1, new float[row])).OrthogonalBasic(floats1));
      }
  
      //矩阵的单位化
      //修改原矩阵
      public static float[][] Unitization(float[][] floats) {
          float[][] floats1 = CopyArry(floats);
          int row = floats1.length;
          for (int i = 0; i < row; i++) {
              float abVe = IntermediateAbsoluteValue(floats1, i);
              for (int i1 = 0; i1 < row; i1++) {
                  floats1[i1][i] = floats1[i1][i] / abVe;
  
              }
          }
  
          return floats1;
      }
      //定义单位化中间方法
  
      /**
       * @param floats 需要传入的数组
       * @param index  数组的列
       * @return 返回该列的 单位化数值
       * 不修改原矩阵
       */
      public static float IntermediateAbsoluteValue(float[][] floats, int index) {
          float[][] floats1 = CopyArry(floats);
          int row = floats1.length;
          int index1 = index;
          float abVe = 0;
          while (index == index1) {
              for (int i = 0; i < row; i++) {
                  abVe += floats1[i][index] * floats1[i][index];
              }
              index++;
          }
  
          return (float) Math.sqrt(abVe);
  
      }
  
      //定义数组的加法
  
      /**
       * @param floats1 传入的第一个数组
       * @param floats2 传入的第二个数组
       * @return 返回一个新的数组，不对原有的参数地址内容进行修改，是一个可靠的方法
       */
      public static float[] DeterminAntddition(float[] floats1, float[] floats2) {
          int row = floats1.length;
          float[] floats = new float[row];
          for (int i = 0; i < row; i++) {
              floats[i] = floats1[i] + floats2[i];
          }
  
          return floats;
      }
  
      //求解逆矩阵
      public Marix_2X2 get_inverse_2() {
  
          Marix_2X2 m1 = new Marix_2X2(this.data);
  
          if (null != this.data) {
  
              int temp = 0;
  
              float[] onwResult = this.data;
  
              temp = isAllZero(temp, onwResult);
  
              if (temp == onwResult.length) {
                  m1.flag = false;
              } else {
  
                  float[][] floats = new float[this.m - 1][this.n];
  
                  float[][] floats2 = one2Two(m1.getData(), floats);
  
                  int row = floats2.length;
                  float[][] floats1 = CopyArry(floats2);
                  float[][] floats6 = new float[row][row];
                  float[][] floats7 = AdjointMatrix(floats1);
                  for (int i = 0; i < row; i++) {
                      for (int i1 = 0; i1 < row; i1++) {
                          floats6[i][i1] = floats7[i][i1] / ArrayCount(floats1, row);
                      }
                  }
  
                  float[] result = two2One(floats6, onwResult);
  
                  m1.setData(result);
  
              }
              return m1;
          } else {
  
              System.out.println("为传入合法的数据....");
  
              return null;
          }
      }
  
      private static int isAllZero(int temp, float[] onwResult) {
  
          for (int i = 0; i < onwResult.length; i++) {
              if (onwResult[i] == 0) {
                  temp++;
              }
          }
          return temp;
      }
  
      private static boolean isAllZero(float[][] onwResult) {
          int temp = 0;
  
          for (float[] floats : onwResult) {
              for (float aFloat : floats) {
                  if (aFloat == 0) {
                      temp++;
                  }
              }
          }
  
          if (temp == onwResult.length) {
              return true;
          } else {
              return false;
          }
      }
  
      //矩阵的复制
      public static float[][] CopyArry(float[][] floats) {
          int row = floats.length;
          float[][] floats1 = new float[row][row];
          for (int i = 0; i < row; i++) {
              for (int i1 = 0; i1 < row; i1++) {
                  floats1[i][i1] = floats[i][i1];
              }
          }
          return floats1;
      }
  
      //矩阵求伴随矩阵
      public static float[][] AdjointMatrix(float[][] floats) {
  
          int row = floats.length;
          float[][] floats1 = CopyArry(floats);
  
          float[][] floats4 = new float[row][row];
          for (int i = 0; i < row; i++) {
              for (int i1 = 0; i1 < row; i1++) {
  
                  floats4[i1][i] = (-1) * (((i + i1) % 2) == 1 ? 1 : -1) * ArrayCount(RemoveRC(floats1, row, i, i1), row - 1);
              }
          }
          return floats4;
      }
  
      //去掉固定的行和列的行列式
      public static float[][] RemoveRC(float[][] floats, int n, int p, int q) {
          float[][] floats1 = new float[n][n];
          float[][] floats2 = new float[n - 1][n - 1];
          ArrayList<Float> arrayList = new ArrayList<>((n - 1) * (n - 1));
          for (int i = 0; i <= n - 1; i++) {
              for (int i1 = 0; i1 <= n - 1; i1++) {
                  floats1[i][i1] = floats[i][i1];
              }
  
          }
          for (int i = 0; i <= n - 1; i++) {
              for (int i1 = 0; i1 <= n - 1; i1++) {
                  if (i == p || i1 == q) {
  
                  } else {
                      arrayList.add(floats[i][i1]);
  
                  }
              }
  
          }
          Object[] objects = arrayList.toArray();
          int index = 0;
          for (int i = 0; i < n - 1; i++) {
              for (int i1 = 0; i1 < n - 1; i1++) {
                  floats2[i][i1] = (float) objects[index];
                  index++;
  
              }
  
          }
  
          return floats2;
      }
  
      // 计算数组行列式方法
      public static float ArrayCount(float a[][], int n) {
  
          float p = 0;
  
          for (int k = 0; k <= n - 2; k++) {
              for (int r = k + 1; r <= n - 1; r++) {
                  if (a[k][k] == 0) {
                      try {
                          ArrayChange(a, k, n);
                      } catch (Exception e) {
                          System.out.println(e.getMessage());
                          return 0;
                      }
                  }
                  p = -(a[r][k] / a[k][k]);
                  for (int i = k; i <= n - 1; i++) {
                      a[r][i] = a[k][i] * p + a[r][i];
                  }
              }
  
          }
          float result = 1;
          for (int i = 0; i <= n - 1; i++) {
              result *= a[i][i];
  
          }
  
          return result;
      }
  
      //行列式行互换方法
  
      /**
       * @param a 传入的数组
       * @param k 出现问题的元素的行和列的坐标数值
       * @param n 数组的长度 ，虽然是从0 标开始，但是这里仍然使用n来计数
       */
      public static void ArrayChange(float a[][], int k, int n) {
          float b[] = new float[n - k];
          int c = k;
          for (int i = k + 1; i <= n - 1; i++) {
              if (a[i][k] != 0) {
                  c = i;
              }
          }
          if (c == k) {
              throw new RuntimeException("高斯求解失败");
          }
          int w = 0;
          for (int i = k; i <= n - 1; i++) {
              b[w] = a[k][i];
              a[k][i] = a[c][i];
              a[c][i] = b[w];
              w++;
          }
  
      }
  
      //矩阵转置的方法
      public Marix_2X2 Transpose() {
  
          Marix_2X2 marix2X2 = new Marix_2X2(this.data);
  
          float[][] floats1 = new float[this.m - 1][this.n];
  
          float[][] floats2 = one2Two(marix2X2.getData(), floats1);
  
          for (int i = 0; i < floats2.length - 1; i++) {
              for (int j = 0; j < floats2[i].length; j++) {
  
                  float temp = floats2[i][j];
                  floats2[i][j] = floats2[j][i];
                  floats2[j][i] = temp;
              }
          }
  
          float[] floats3 = this.data;
  
          float[] floats = two2One(floats2, floats3);
  
          marix2X2.setData(floats);
  
          return marix2X2;
  
      }
  
      /**
       * 求（h，v）位置的余子式
       *
       * @param matrix
       * @param h
       * @param v
       * @return
       */
      public float[][] confactor(float[][] matrix, int h, int v) {
          float[][] result = new float[matrix.length - 1][matrix[0].length - 1];
          for (int i = 0; i < result.length; i++) {
              if (i < h - 1) {
                  for (int j = 0; j < result[i].length; j++) {
                      if (j < v - 1) {
                          result[i][j] = matrix[i][j];
                      } else {
                          result[i][j] = matrix[i][j + 1];
                      }
                  }
              } else {
                  for (int j = 0; j < result[i].length; j++) {
                      if (j < v - 1) {
                          result[i][j] = matrix[i + 1][j];
                      } else {
                          result[i][j] = matrix[i + 1][j + 1];
                      }
                  }
              }
          }
  
          return result;
      }
  
      private static float[][] getData(Marix_2X2 m8) {
          float[][] floats1 = new float[m8.m - 1][m8.n];
          float[][] floats2 = one2Two(m8.getData(), floats1);
          return floats2;
      }
  
      public static void main(String[] args) {
  
          // 查看矩阵
          Marix_2X2 marix2X2 = new Marix_2X2(new float[]{1, 2, 2, 5});
          marix2X2.showInfo();
  
          // 全为0的矩阵
          Marix_2X2 m1 = new Marix_2X2(new float[]{0, 0, 0, 0});
          Marix_2X2 tmp = m1.get_inverse_2();
          assert tmp != null;
          tmp.showInfo();
  
          // 求矩阵的逆矩阵
          Marix_2X2 m0 = new Marix_2X2(new float[]{1, 2, 2, 5});
          Marix_2X2 tmp0 = m0.get_inverse_2();
          assert tmp0 != null;
          tmp0.showInfo();
  
          // 矩阵的乘法
          Marix_2X2 m2 = new Marix_2X2(new float[]{2, 5, 1, 3});
          Marix_2X2 m3 = new Marix_2X2(new float[]{4, -6, 2, 1});
          m2.get_inverse_2().mul(m3).showInfo();
  
          // 矩阵的复合乘法
          Marix_2X2 m4 = new Marix_2X2(new float[]{1, 4, -1, 2});
          Marix_2X2 m5 = new Marix_2X2(new float[]{3, 1, 0, -1});
          Marix_2X2 m6 = new Marix_2X2(new float[]{2, 0, -1, 1});
          m4.get_inverse_2().mul(m5).mul(m6.get_inverse_2()).showInfo();
  
      }
  
  }
  
  

三、其他相关方法的测试

// 转置
        Marix_2X2 m7 = new Marix_2X2(new float[]{2, 5, -1, 1});
        Marix_2X2 transpose = m7.Transpose();
        transpose.showInfo();

        // 伴随矩阵
        Marix_2X2 m8 = new Marix_2X2(new float[]{2, 5, -1, 1});
        float[][] floats = m8.AdjointMatrix(getData(m8));
        m8.setData(two2One(floats, m8.getData()));
        m8.showInfo();

        // 余子式
        m8.setData(two2One(m8.confactor(getData(m8), 2, 2), m8.getData()));
        m8.Transpose();
        m8.showInfo();

Python版本开发

• 都是面向对象的语言，因此操作步骤也是大同小异。

一、python代码

1、导入 包

# 这个一定要导入，不然的话，是用不了的
import numpy as np

2、创建数组

A = np.array([[1,2],[2,5]])

3、打印数组

# 矩阵信息打印
def showInfo(x):
    print("------------")
    print("矩阵的尺寸为：",np.shape(x)[0],"x",np.shape(x)[1])
    print(x)
    print("------------")

4、求矩阵的逆

# 求逆矩阵
def getInverse(x):

    if(np.all(x==0)):
      print("行列为0,不能求逆矩阵")
    else:
      B = np.linalg.inv(x)
      print("逆矩阵")
      return B

5、矩阵的乘法

# 矩阵乘法
def mul(x,y):
    c = np.matmul(x,y)
    return c

6、完整版

import numpy as np
from numpy import *

# 矩阵信息打印
def showInfo(x):
    print("------------")
    print("矩阵的尺寸为：",np.shape(x)[0],"x",np.shape(x)[1])
    print(x)
    print("------------")

# 求逆矩阵
def getInverse(x):

    if(np.all(x==0)):
      print("行列为0,不能求逆矩阵")
    else:
      B = np.linalg.inv(x)
      print("逆矩阵")
      return B

# 矩阵乘法
def mul(x,y):
    c = np.matmul(x,y)
    return c

def main():
    pass

if __name__ == '__main__':
    main()

    A = np.array([[1,2],[2,5]])
    showInfo(A)

    B = np.array([[0,0],[0,0]])
    getInverse(B)
    H = getInverse(A)
    showInfo(H)

    print("-----矩阵乘法-------")

    C = np.array([[2,5],[1,3]])
    D = np.array([[4,-6],[2,1]])

    m2 = getInverse(C)
    result1 = mul(m2,D)
    showInfo(result1)

    print("-----混合乘法-------")
    E = np.array([[1,4],[-1,2]])
    F = np.array([[3,1],[0,-1]])
    G = np.array([[2,0],[-1,1]])

    m3 = getInverse(E)
    result2 = mul(m3,F)
    m4 = getInverse(G)
    result3 = mul(result2,m4)
    showInfo(result3)

7、测试结果

• 明显可以看到python的写法比Java的更加简洁，容易理解，因此，这种题目如果可以自己选择，最好使用python开发。

8、拓展其他功能

# 求单位矩阵
def singleArray(x):
    F = np.eye(x)
    return F

# 矩阵转置
def transArray(x):
    H = x.T
    return H

# 计算行列式的值
def getValue(x):
    H = np.linalg.det(x)
    return H

# A的伴随矩阵
def adjointMatrix(A):
    n,_=A.shape                             #获取阶数n
    Am=np.zeros((n,n))                      #Am初始化为零阵
    for i in range(n):                      #每一行
        for j in range(n):                  #每一列
            Am[i,j]=Aij(A,i,j)              #伴随阵元素
    return Am.T

#代数余子式
def Aij(A,i,j):
    up=np.hstack((A[:i,:j],A[:i,j+1:]))     #横向连接上方片段
    lo=np.hstack((A[i+1:,:j],A[i+1:,j+1:])) #横向连接下方片段
    M=np.vstack((up,lo))                    #纵向连接
    return ((-1)**(i+j))*np.linalg.det(M)   #代数余子式

# 求代数余子式
def cofactor(matrix, i, j):
    m = np.delete(matrix, i, axis=0)
    m = np.delete(m, j, axis=1)
    return np.linalg.det(m)

def cofactor_matrix(matrix):
    n = matrix.shape[0]
    cofactors = np.zeros((n, n))

    for i in range(n):
        for j in range(n):
            cofactors[i, j] = (-1) ** (i + j) * cofactor(matrix, i, j)

    return cofactors

• 测试代码

  if __name__ == '__main__':
  
      print("-----单位矩阵-------")
      H =np.array([[1,2,3],[4,5,6],[6,1,3]])
      lie = np.shape(H)[1]
      result4=singleArray(lie)
      showInfo(result4)
  
      print("-----转置-------")
      result5=transArray(H)
      showInfo(result5)
  
      print("-----计算行列式的值-------")
      I =np.array([[1,1,1],[1,1,0],[1,1,3]])
      result6=getValue(H)
      print(result6)
  
      print("-----伴随矩阵-------")
       #设置矩阵A
      A1=np.array([[1,2,3],[2,2,1],[3,4,3]])
      Am=adjointMatrix(A1)                         #A的伴随阵
      print("A∗=",Am)
  
      print("AA∗=",np.matmul(A1,Am))
  
      # 也是求伴随,结果跟上边不一样
      B1=np.linalg.inv(A1)
      A_bs = B1*np.linalg.det(A)
      print(A_bs)
  
      print("-----求代数余子式-------")
  
      A3 = np.array([[1, 2, 3],
                [4, 5, 6],
                [7, 8, 9]])
  
       # 求解余子式矩阵
      C3 = cofactor_matrix(A3)
      print(C3)
  

• 测试结果