[NLP复习笔记] 基于负采样的 Skip-gram 及 SGD 训练公式推导

1. one-hot 向量

我们先了解一下 \(\text{one-hot}\) 向量。\(\text{one-hot}\) 编码是表示分类变量的常见方法，尤其在数据预处理和机器学习的特征工程中。一个 \(\text{one-hot}\) 向量是一个其中只有一个元素是 1，其余为 0 的向量。

假设存在一个单词集合：\(\{\text{marisa, reimu, renko, hearn}\}\)，可以将这些单词进行索引映射：

\[\begin{split}
\text{marisa} \rightarrow 0
\\
\text{reimu} \rightarrow 1
\\
\text{renko} \rightarrow 2
\\
\text{hearn} \rightarrow 3
\end{split}
\]

那么，这些单词经过 \(\text{one-hot}\) 编码的向量如下：

\[\begin{split}
& \text{marisa}: [1, 0, 0, 0]
\\
& \text{reimu}: [0, 1, 0, 0]
\\
& \text{renko}: [0, 0, 1, 0]
\\
& \text{hearn}: [0, 0, 0, 1]
\end{split}
\]

显然，每个位置被看作一个特征，这个特征只能是 1（存在）或者 0（不存在）。

但是，对于包含大量唯一词汇的大型语料库而言， \(\text{one-hot}\) 编码会产生 极大的稀疏矩阵，每一个单词对应的词向量都是 \(|V|\) 维的，使得 维度很高，导致计算效率低下。

而且 \(\text{one-hot}\) 编码的词向量之间都是等距的，每个词语的向量与其他词语的向量都是正交的关系，这意味着它们 不携带任何词语间的相似性信息。

\(\text{one-hot}\) 编码现在依然有比较广泛的应用，但在一些自然语言处理问题中，为了避免上述的限制，会采用更加高级的技术，就比如 \(\text{Word2Vec}\)。

---

2. Word2Vec

2.1 Word2Vec 介绍

\(\text{Word2Vec}\) 模型通过训练神经网络，为每个单词构建一个密集且连续的向量。这些向量被称为 词嵌入（word embeddings），它们捕捉大量关于单词的语义和句法信息。每个单词在多维空间中被表示为一个向量，向量中的每个维度代表词义的不同方面，具体每个维度代表什么并不是人为定义的，而是通过 模型学习得到 的。

例如，经过训练后，单词 \(\text{marisa}\) 最终对应的词向量是 一个 \(d\) 维的向量，有可能是如下的形式：

\[vec_{\text{marisa}} =
\begin{bmatrix}
0.1
\\
1.5
\\
\vdots
\\
0.7
\end{bmatrix}
\]

\(vec\) 就是 目标单词的词向量。这里的维度 \(d\) 是 人为设定的一个超参数，表示我们需要将单词映射到一个 \(d\) 维的向量空间，决定了 词向量的特征数量，也就是我们想要 得到的词向量的大小。

通过 \(\text{Word2Vec}\) 得到的词向量 拥有相似上下文的词在空间中的位置，能够捕捉单词之间的语义关系。

从维度上，提取的 \(d\) 个维度特征，可以一定程度上避免维度过高的情况；从语义上，携带上下文信息，可以表示出近义词的相似性。

2.2 Skip-gram 与 CBOW

\(\text{Word2Vec}\) 模型包括输入层、隐藏层和输出层。模型框架根据输入输出的不同，主要包括 \(\text{Skip-gram}\) 和 \(\text{CBOW}\) 两种模型。

\(\text{Skip-gram}\) 模型: 用一个词语作为输入，来预测其上下文。模型的目标是 最大化在给定目标单词的情况下上下文单词出现的概率，也就是 计算其他单词出现在目标单词周围的概率。

\(\text{CBOW}\) 模型: 用一个词语的上下文作为输入，来预测这个词语。模型的目标是最大化上下文单词出现时目标单词的条件概率。

本篇文章将会介绍基于 \(\text{Negative Sampling}\) 的 \(\text{Skip-gram}\) 模型。（\(\text{Negative Sampling}\) 也就是 负采样，是 \(\text{Word2Vec}\) 模型训练的加速策略之一）

---

3. 基于 Negative Sampling 的 Skip-gram

3.1 Skip-gram 模型

\(\text{Skip-gram}\) 模型输入层 \(x\) 只有一个单词，输出层 \(y\) 为多个单词，其基本结构如下：

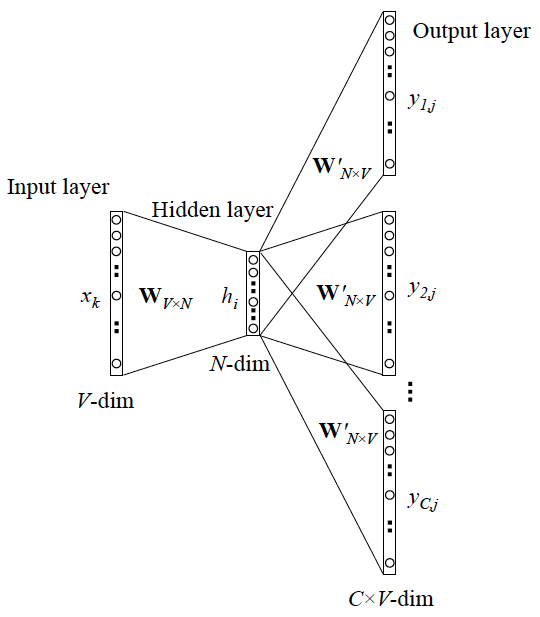
下面的 \(d\) 对应图中的 \(N\)。

• 输入层 \(x\)：一个 \(1 \times V\) 的 \(\text{one-hot}\) 向量，\(V\) 为词汇表大小。表示一个单词，也是我们的 目标词。

• \(W\) 矩阵：输入层到隐藏层之间 \(V \times d\) 的参数矩阵，包含了模型使用的所有词向量，目的是为了将输入层的 \(\text{one-hot}\) 向量映射到嵌入向量空间，也就是 \(d\) 维空间。

• 隐藏层 \(h\)：一个 \(1 \times d\) 的特征向量，其实也就是当前的 目标词对应的词向量 。

• \(W^{'}\) 矩阵：隐藏层到输出层之间的 \(d \times V\) 的参数矩阵，用来将隐藏层的表示转换到输出空间。也表示了所有单词的词向量，将于 目标词词向量做内积。

• 输出层 \(o\)：一个 \(1 \times V\) 的向量。经过 \(h \times W^{'}\) 后（做内积之后）产生一个相似度向量，向量中 每个元素 表示词汇表 每个单词 的 在目标词上下文出现 的 原始概率。最后要经过一个 激活层 得到 真实概率。对于 多分类 问题，常常采用 \(\text{softmax}\) 函数；对于 二分类 问题，则一般采用 \(\text{sigmoid}\) 函数。（注意，这里的输出层并非图中最终的输出，只是一个概率的分布）

PS: 在后面的问题中，将会采用 \(\text{sigmoid}\) 函数。

• 输出单词 \(y\)：\(C\) 个单词的 \(\text{one-hot}\) 向量，其中 \(C\) 表示采用的 上下文窗口的大小。根据输出层 \(o\) 的概率分布，选取 前 \(C\) 大概率 的单词作为最终预测的 目标词 \(x\) 的上下文单词 \(y\)。

下图是一个上下文窗口典型示例：

3.2 Negative Sampling

传统的神经语言模型需要在每一步对全词汇表进行运算，而 \(\text{Negative Sampling}\)（负采样）只在更新权重时考虑一个小的负样本集合，也就是随机选择一个负单词集合（也就是若干非上下文的单词组成的一个子集）。这样，目标就转化为 最大化正样本的概率，同时最小化负样本的概率。

由此我们可以得到如下定义：

• 样本概率

  \[P(+ | w, c) = \sigma (c \cdot w)
  \]

  其中 \(w\) 表示 目标词对应的词向量，\(c\) 表示 目标词的上下文对应的词向量。

  \(\sigma\) 表示 \(\text{sigmoid}\) 函数，\(c \cdot w\) 是两个词向量的内积。

• 正样本似然函数

  \[\prod P(+ | w, c_{\text{pos}})
  \]

• 负样本似然函数

  \[\prod P(- | w, c_{\text{neg}})
  \]

我们需要最大化正样本的概率，同时最小化负样本的概率，所以，可以转化为最大化下式：

\[\prod P(+ | w, c_{\text{pos}}) \prod (1 - P(- | w, c_{\text{neg}}))
\]

为了计算方便，我们可以取对数，得到对数似然函数：

\[\mathcal{L} = \text{log}(\prod P(+ | w, c_{\text{pos}}) \prod (1 - P(- | w, c_{\text{neg}})))
\]

为了后续方便训练，我们可以变成最小化如下形式 (在前面加一个负号)：

\[L = - \text{log}(\prod P(+ | w, c_{\text{pos}}) \prod (1 - P(- | w, c_{\text{neg}})))
\]

由 \(\text{sigmoid}\) 函数 \(f(x) = \frac{1}{1 + e^{-x}}\) 得：

\[\begin{split}
L &= - \text{log}(\prod \sigma (c_{\text{pos}} \cdot w) \prod \sigma(- c_{\text{neg}} \cdot w))
\\\\
&= - \left [ \sum \text{log} \; \sigma(c_{\text{pos}} \cdot w) + \sum \text{log} \; \sigma(- c_{\text{neg}} \cdot w) \right ]
\end{split}
\]

一般情况下使用 \(\text{SGD}\) （随机梯度下降法）来进行学习，故只需要知道对一个正样本 \((w, c_{\text{pos}})\) 的目标函数。假设我们随机选取 \(k\) 个负样本单词作为负采样集合，则有如下形式：

\[L = - \left [ \text{log} \; \sigma(c_{\text{pos}} \cdot w) + \sum_{i=1}^k \text{log} \; \sigma(- c_{\text{neg}_{i}} \cdot w) \right ]
\]

这就是我们最终要 最小化得目标函数 \(L\) 。

3.3 参数求导

我们最终需要得到最优的 \(c_\text{pos}\) 、\(c_{\text{neg}}\) 以及 \(w\) 参数，由 \(\text{SGD}\) 算法（应该没有人不懂这个算法吧），我们要分别对这些参数求导。

目标函数中有 \(\text{sigmoid}\) 函数，故在求导之前，我们先看一下 \(\text{sigmoid}\) 函数的求导，以便后续化简。

\(\text{sigmoid}\) 函数如下：

\[\sigma(x) = \frac{1}{1 + e^{-x}}
\]

我们先对其进行变形，得：

\[\begin{split}
\sigma(x) &= \frac{1}{1 + e^{-x}}
\\\\
&= \frac{e^x}{e^x + 1}
\\\\
&= 1 - (e^x + 1)^{-1}
\end{split}
\]

由此可得 \(\text{sigmoid}\) 的导数如下：

\[\begin{split}
\frac{\text{d} \sigma}{\text{d} x} &= (e^x + 1)^{-2} e^x
\\\\
&= [e^x(1 + e^{-x})]^{-2} e^x
\\\\
&= (1 + e^{-x})^{-2} e^{-2x} e^x
\\\\
&= (1 + e^{-x})^{-1} \cdot \frac{e^{-x}}{1 + e^{-x}}
\\\\
&= \sigma(x) \cdot (1 - \sigma(x))
\end{split}
\]

我们可以再看下 \(\sigma(-x)\) 的导数。显然 \(\text{sigmoid}\) 函数满足 \(\sigma(-x) = 1 - \sigma(x)\)，所以\(\sigma(-x)\) 的导数就很简单了，就是 \(-\sigma(x) \cdot (1 - \sigma(x))\)

后面再对各个参数求导就比较清晰易懂了，具体过程如下(对数看作取 \(\text{ln}\) 函数)：

• 对 \(c_{\text{pos}}\) 求导

  这里使用了 链式求导法则。

  \[\begin{split}
  \frac{\partial L}{\partial c_{\text{pos}}} &= \frac{\partial}{\partial c_{\text{pos}}}(- \left [ \text{log} \; \sigma(c_{\text{pos}} \cdot w) + \sum_{i=1}^k \text{log} \; \sigma(- c_{\text{neg}_i} \cdot w) \right ])
  \\\\
  &= - \frac{\partial L}{\partial \sigma(c_{\text{pos}} \cdot w)} \frac{\partial \sigma(c_{\text{pos}} \cdot w)}{\partial c_{\text{pos}}}
  \end{split}
  \]

  其中前半部分为：

  \[\frac{\partial L}{\partial \sigma(c_{\text{pos}} \cdot w)} = \frac{1}{\sigma(c_{\text{pos}} \cdot w)}
  \]

  后半部分为：

  \[\frac{\partial \sigma(c_{\text{pos}} \cdot w)}{\partial c_{\text{pos}}} = \sigma(c_{\text{pos}} \cdot w) \cdot (1 - \sigma(c_{\text{pos}} \cdot w))\;w
  \]

  最后结合起来得到 \(\frac{\partial L}{\partial c_{\text{pos}}}\)（记得最全面有一个负号） ：

  \[\begin{split}
  \frac{\partial L}{\partial c_{\text{pos}}} &= - \frac{1}{\sigma(c_{\text{pos}} \cdot w)} \; \sigma(c_{\text{pos}} \cdot w) \; (1 - \sigma(c_{\text{pos}} \cdot w)) \; w
  \\\\
  &= \left [ \sigma(c_{\text{pos}} \cdot w) - 1 \right] w
  \end{split}
  \]

• 对 \(c_{\text{neg}}\) 求导

  使用 链式求导法则

  \[\begin{split}
  \frac{\partial L}{\partial c_{\text{neg}}} &= \frac{\partial}{\partial c_{\text{neg}}}(- \left [ \text{log} \; \sigma(c_{\text{pos}} \cdot w) + \sum_{i=1}^k \text{log} \; \sigma(- c_{\text{neg}_i} \cdot w) \right ])
  \\\\
  &= - \sum_{i=1}^k \frac{\partial L}{\partial \sigma(- c_{\text{neg}_i} \cdot w)} \frac{\partial \sigma(- c_{\text{neg}_i} \cdot w)}{\partial c_{\text{neg}_i}}
  \end{split}
  \]

  前半部分为：

  \[\frac{\partial L}{\partial \sigma(- c_{\text{neg}_i} \cdot w)} = \frac{1}{\sigma(- c_{\text{neg}_i} \cdot w)}
  \]

  后半部分为：

  \[\begin{split}
  \frac{\partial \sigma(- c_{\text{neg}_i} \cdot w)}{\partial c_{\text{neg}_i}} &= -\sigma(c_{\text{neg}_i} \cdot w) \; (1 - \sigma(c_{\text{neg}_i} \cdot w)) \; w
  \end{split}
  \]

  由于 \(\sigma(-x) = 1 - \sigma(x)\)，我们可以把 \((1 - \sigma(c_{\text{neg}_i} \cdot w))\) 换成 \(\sigma(- c_{\text{neg}_i} \cdot w)\) 便于后续化简：

  \[\frac{\partial \sigma(- c_{\text{neg}_i} \cdot w)}{\partial c_{\text{neg}_i}} = - \sigma(c_{\text{neg}_i} \cdot w) \; \sigma(- c_{\text{neg}_i} \cdot w) \; w
  \]

  将两个部分结合起来，得到 \(\frac{\partial L}{\partial c_{\text{neg}}}\)（记得最全面有一个负号）：

  \[\begin{split}
  \frac{\partial L}{\partial c_{\text{neg}}} &= - \sum_{i=1}^k \frac{1}{\sigma(- c_{\text{neg}_i} \cdot w)} \; \left [ - \sigma(c_{\text{neg}_i} \cdot w) \; \sigma(- c_{\text{neg}_i} \cdot w) \; w \right ]
  \\\\
  &= \sum_{i=1}^k \frac{1}{\sigma(- c_{\text{neg}_i} \cdot w)} \; \left [ \sigma(c_{\text{neg}_i} \cdot w) \; \sigma(- c_{\text{neg}_i} \cdot w) \; w \right ]
  \\\\
  &= \sum_{i=1}^k \sigma(c_{\text{neg}_i} \cdot w) \; w
  \\\\
  &= [\sigma(c_{\text{neg}} \cdot w)] \; w
  \end{split}
  \]

• 对 \(w\) 求导

  对前面两个参数进行求导后，对 \(w\) 求导就方便多了。

  \[\frac{\partial L}{\partial w} = - \left [ \frac{\partial}{\partial w}(\text{log} \; \sigma(c_{\text{pos}} \cdot w)) + \frac{\partial}{\partial w}(\sum_{i=1}^k \text{log} \; \sigma(- c_{\text{neg}_i} \cdot w)) \right ]
  \]

  对于前半部分，由

  \[\frac{\partial}{\partial w} \sigma(c_{\text{pos}} \cdot w) = \sigma(c_{\text{pos}} \cdot w) \; (1 - \sigma(c_{\text{pos}} \cdot w)) \; c_{\text{pos}}
  \]

  可得

  \[\begin{split}
  \frac{\partial}{\partial w}(\text{log} \; \sigma(c_{\text{pos}} \cdot w)) &= \frac{1}{\sigma(c_{\text{pos}} \cdot w)} \sigma(c_{\text{pos}} \cdot w) \; (1 - \sigma(c_{\text{pos}} \cdot w)) \; c_{\text{pos}}
  \\\\
  &= [1 - \sigma(c_{\text{pos}} \cdot w)] \; c_{\text{pos}}
  \end{split}
  \]

  对于后半部分，由

  \[\frac{\partial}{\partial w} \sigma(- c_{\text{neg}_i} \cdot w) = \sigma(- c_{\text{neg}_i} \cdot w) \; (1 - \sigma(- c_{\text{neg}_i} \cdot w) \; (-c_{\text{neg}_i})
  \]

  得

  \[\begin{split}
  \frac{\partial}{\partial w}(\text{log} \; \sigma(-c_{\text{neg}_i} \cdot w)) &= \frac{1}{\sigma(-c_{\text{neg}_i}\cdot w)} \sigma(- c_{\text{neg}_i} \cdot w) \; (1 - \sigma(- c_{\text{neg}_i} \cdot w) \; (-c_{\text{neg}_i})
  \\\\
  &= - [1 - \sigma(c_{\text{neg}_i} \cdot w)] \; c_{\text{neg}_i}
  \\\\
  &= - [\sigma(c_{\text{neg}_i}\cdot w)] \; c_{\text{neg}_i}
  \end{split}
  \]

  最后结合起来，得到 \(\frac{\partial L}{\partial w}\)（记得最全面有一个负号）：

  \[\frac{\partial L}{\partial w} = [ \sigma(c_{\text{pos}} \cdot w) - 1] \; c_{\text{pos}} + \sum_{i=1}^k [\sigma(c_{\text{neg}_i}\cdot w)] \; c_{\text{neg}_i}
  \]

以上就是对参数求导的全部推导过程。

3.4 SGD 更新公式

将上面的导数套用到 \(\text{SGD}\) 更新公式就可以了。最后简单写一下更新公式：

\[c_{\text{pos}}^{t + 1} = c_{\text{pos}}^{t} - \eta \left [ \sigma(c_{\text{pos}}^t \cdot w^t) - 1 \right] w^t
\]

\[c_{\text{neg}}^{t + 1} = c_{\text{neg}}^{t} - \eta \left [ \sigma(c_{\text{neg}}^t \cdot w^t) \right] w^t
\]

\[w^{t + 1} = w^t - \eta \left ( [ \sigma(c_{\text{pos}} \cdot w) - 1] \; c_{\text{pos}} + \sum_{i=1}^k [\sigma(c_{\text{neg}_i}\cdot w)] \; c_{\text{neg}_i} \right )
\]

经过不断迭代更新后，最后得到最优的 \(c_\text{pos}\) 、\(c_{\text{neg}}\) 以及 \(w\) 参数，也就是最终的 上下文词向量 \(c\) 和 目标词对应的词向量 \(w\) 。

最后，通常会将两个词向量进行相加，来表述单词。例如第 \(i\) 个单词就可以表示为 \(w_i + c_i\) 。

---

参考

【词向量基础】：one-hot

全面理解word2vec

Word2Vec介绍：直观理解skip-gram模型

深入浅出Word2Vec原理解析

[NLP] 秒懂词向量Word2vec的本质

sigmoid函数求导-只要四步