曲线艺术编程 coding curves 第九章 旋轮曲线（ROULETTE CURVES）

第九章 旋轮曲线（ROULETTE CURVES）

原作：Keith Peters https://www.bit-101.com/blog/2022/11/coding-curves/

译者：池中物王二狗(sheldon)

源码：github: https://github.com/willian12345/coding-curves

曲线艺术编程系列第 9 章

一开始我本章标题我打算使用“次摆线与摆线（旋轮线）”。我想它们是两种不同类型的曲线，虽然有点儿联系。但随着了解的深入，我有点儿凌乱了。事实上摆线是一类非常特别的次摆线。我会原谅我自己的。这是维基百科上它们的定义：

在几何上，次摆线（trochoid 原自古希腊语 trochos ‘wheel’）是一个圆延一条直线滚动一圈形成的旋转曲线。

在几何上， 摆线追踪在圆上的一个点，圆延直线滚动后形成的曲线。

它们不仅不是两个不同的东西，从描述上看它们几乎是同一个东西。细节决定成败。让我们开始探索吧。

有三种不同的次摆线：

• 普通次摆线（也称摆线）
• Prolate trochoids 长幅摆线
• Curtate trochoids 短幅摆线

除此之外，还有一些相关的曲线，大概覆盖以下几种：

Epitrochoids 长短辐外摆线

Hypotrochoids 长短辐内摆线

Epicycloids 外摆线

Hypocycloids 内摆线

Involutes 渐伸线

它们组合在一起就是旋轮曲线家族了。在这章除 Involutes 渐伸线外其它都将涉及到。

讲了了大堆有的没的，先从次摆线开始，让我们一一把它们搞清楚。

Trochoids 次摆线

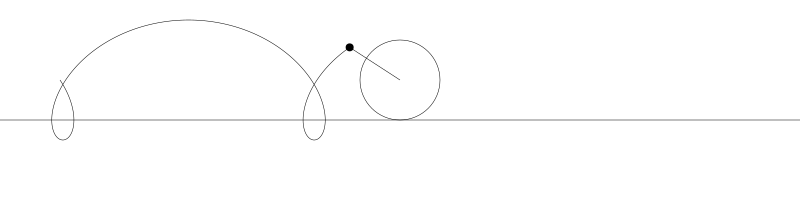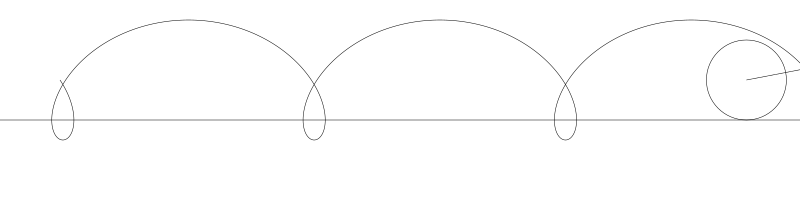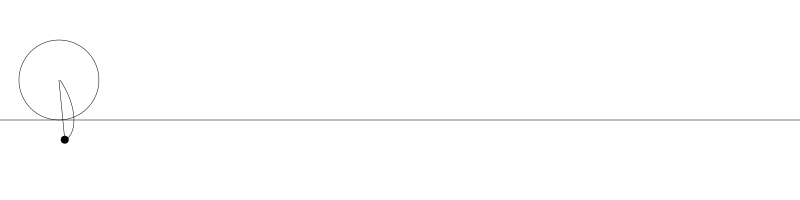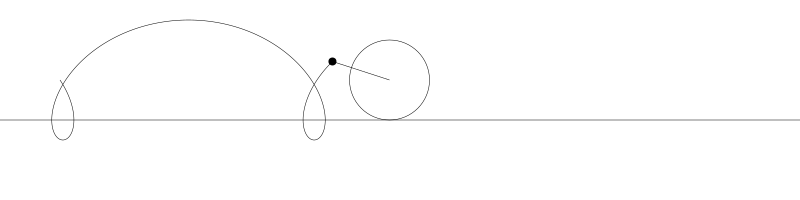
就像上面描述的，一条次摆线就是一个圆在直线上滚动形成的旋转曲线。在编码之前先把它可视化看看：

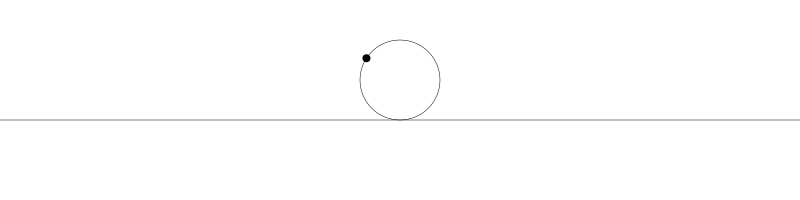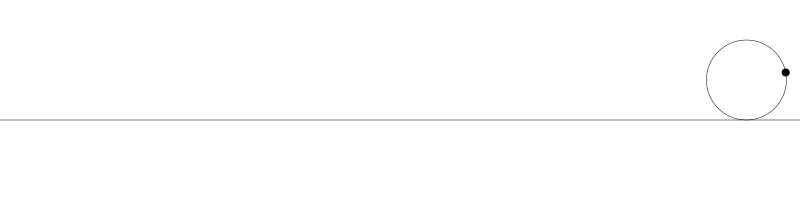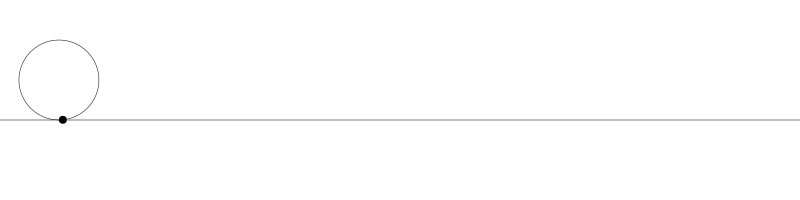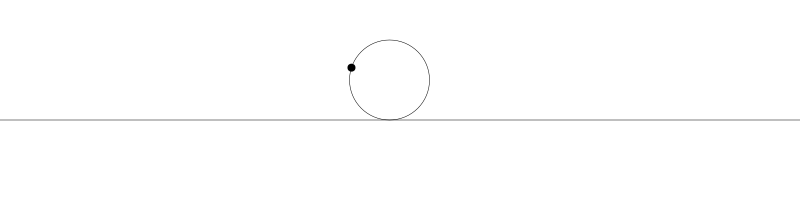
如果我们追踪圆周上的那个黑点...

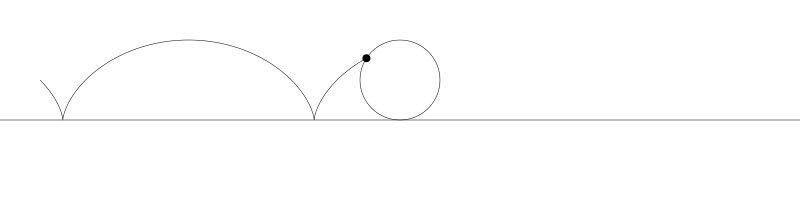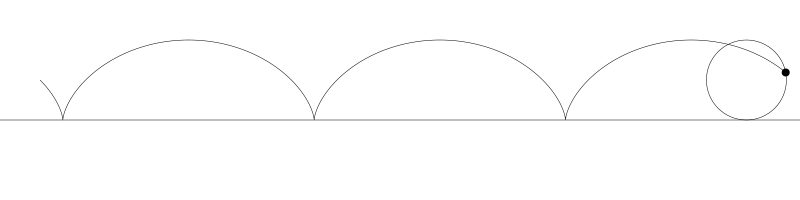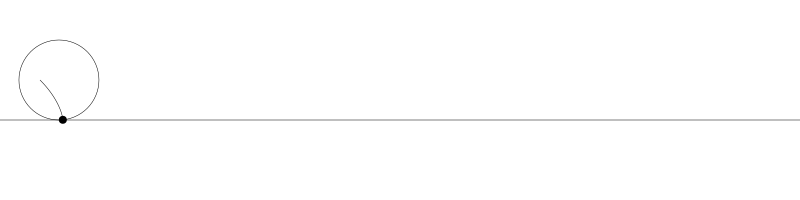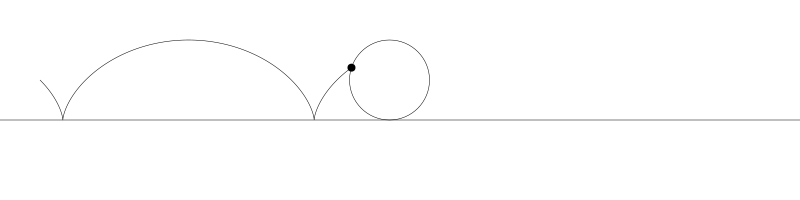
... 新的曲线就是次摆线。事实上由于是绘制点依赖于圆周，所以也称为普通摆线或圆滚线。

如果将圆周上的点延伸超过圆周，那么我们就得到长幅次摆线（Prolate trochoid）。

如果黑点在圆内部，它就是短幅次摆线（Curtate trochoids)。

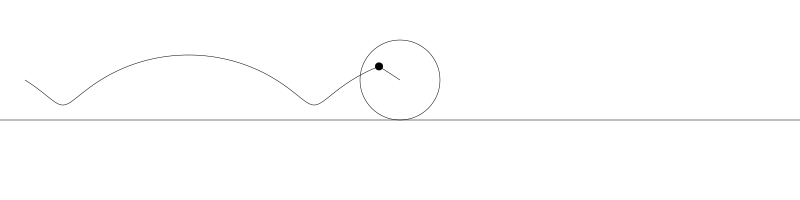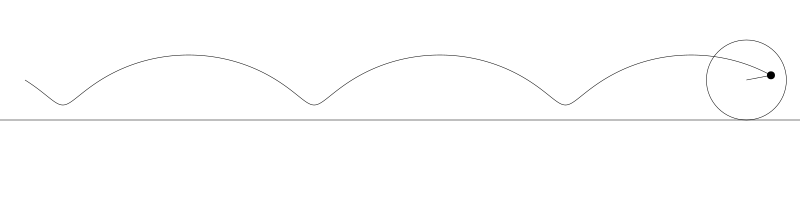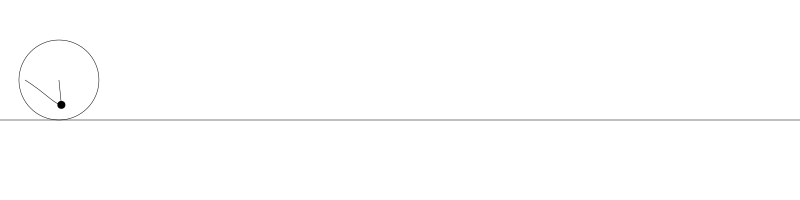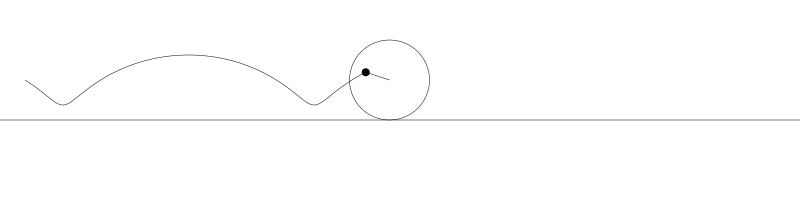
为了做出这些动画，我让圆从左向右运动，计算出每个位置上圆的旋转角度，用 sine 和 cosine 基于圆的位置与旋转角度计算出点的位置，然后用这些点画出线。但对于次摆线其实有更直接的公式

x = a * t - b * sin(t)
y = a - b * cos(t)

t 是圆的旋转角度，它可以无限增长， a 是圆的半径， b 是圆心点至绘制点的距离 - 可以说是那个点的半径。让我们把它实现出来：

width = 800
height = 300
canvas(width, height)

translate(0, height/2)
scale(1, -1)
moveTo(0, 0)
lineTo(width, 0)
stroke()

a = 20.0
b = 20.0
res = 0.05

for (t = 0.0; t < width; t += res) {
    x = a * t - b * sin(t)
    y = a - b * cos(t)
    lineTo(x, y)
}
stroke()

公式是基于笛卡尔坐标的，我们要将 y 轴移至 canvas 中心，并将 y 轴翻转。

然后画一条直线从 y 轴中心穿过用于表示圆滚动时的“地面”。你可以画也可以选择不画。

我们将 a 和 b 都设为 20， 这样就可以得到摆线（译者者：普通旋转线）了。我们循环将从 0 至 canvas 的宽度用于变量 t, 应用公式连接至计算出的结果点。

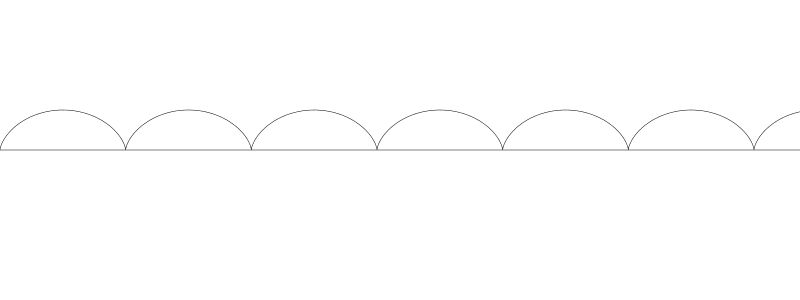
如果将 b 提高到 60， 我们就得到了长幅摆线

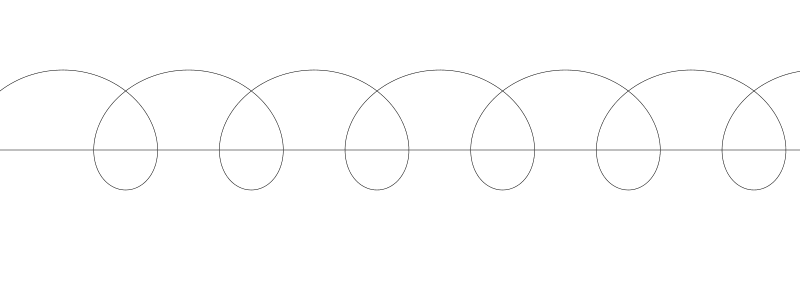
如果将 b 减小到 10， 我们就得到了短幅摆线。

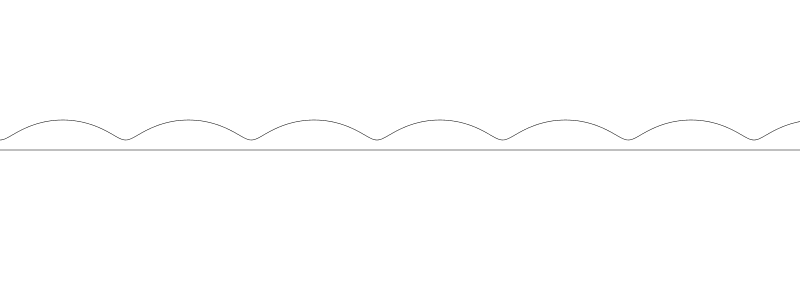
我不知道长幅摆线和短幅摆线的用词是否准确，但听起来挺酷。

这就是全部关于次摆线的内容。试试给 a 和 b 设不同的值，或者你自己改一下其它值，我就不再再多讲了。因为下面还留有很多旋轮曲线需要探讨。

中心次摆线

接下来我们要聚焦于被称为中心次摆线的四种曲线。与延直线滚动不同，它是延另一个圆滚动，可能是延那个圆圆内部滚动也可能是延那个圆的外部滚动。

四类分别是：

• Epicycloids 外摆线 - 延一个圆外部滚动的圆，圆周上某一点轨迹形成的曲线。
• Epitrochoids 长短辐外摆线 - 与上面一个一样，但这个点是不在圆周上，而是在圆外或圆内，与短幅次摆线与长幅次摆线一样。
• Hypocycloids 内摆线 - 延一个圆内部滚动的圆，圆周上某一点轨迹形成的曲线。
• Hypotrochoids 长短辐内摆线 - 与上面那个一样，但这个点是不在圆周上，而是在圆外或圆内

除此之外，还有一些曲线也是属于上面曲线的一种变体，只是形成曲线的两个圆半径有特殊的比例关系。我们稍后会看介绍一些。

Epitrochoids 长短辐外摆线

首先，让我们将一个圆延另一个圆外滚动可视化

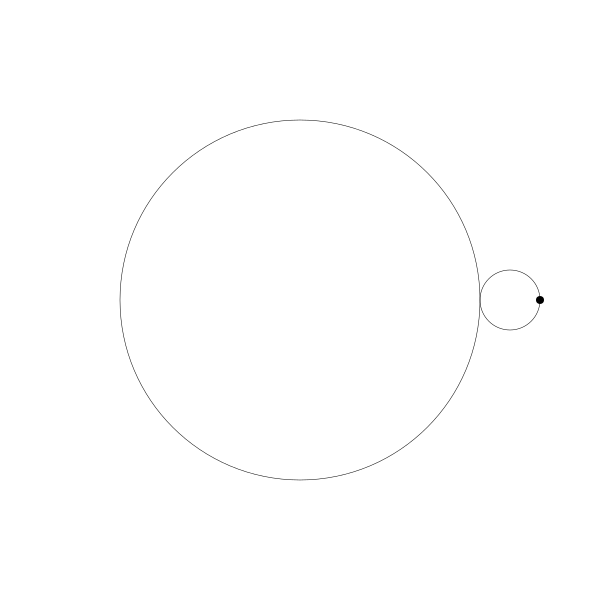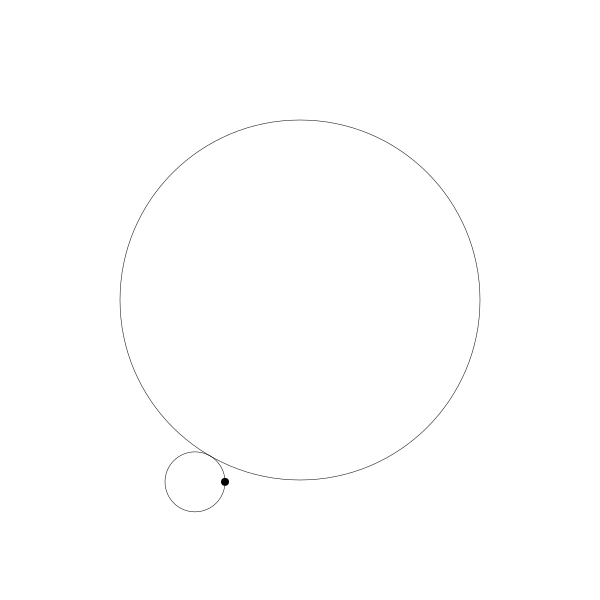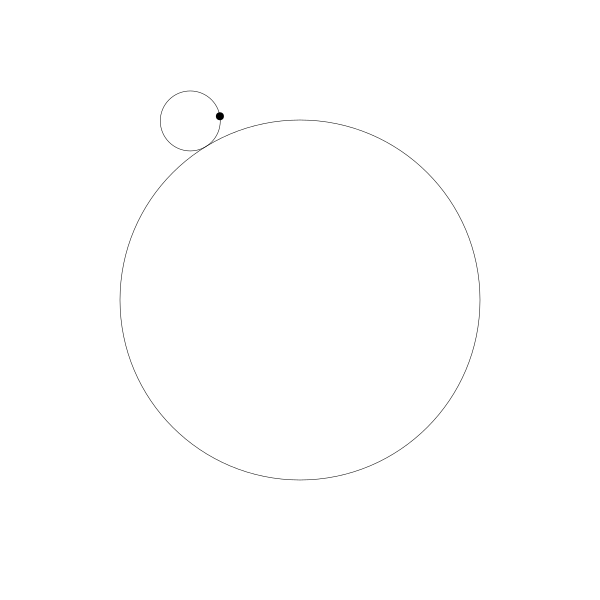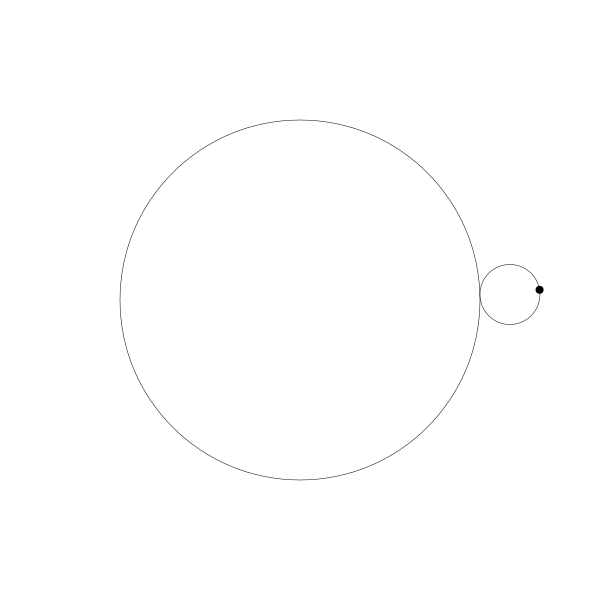
再追踪一下那个黑色的点的绘制结果

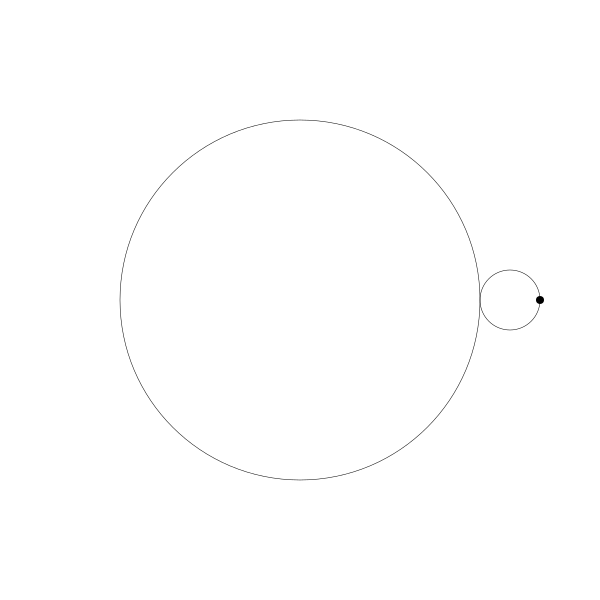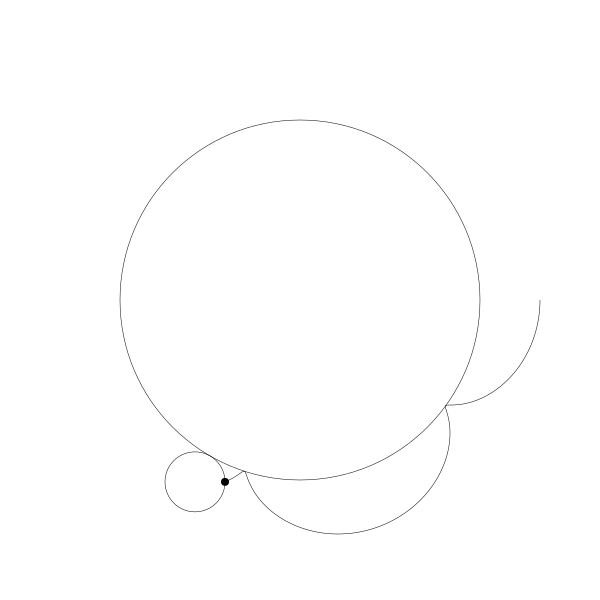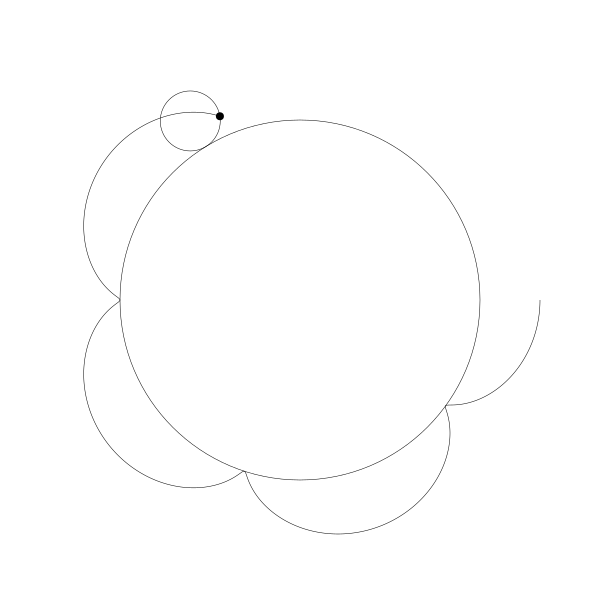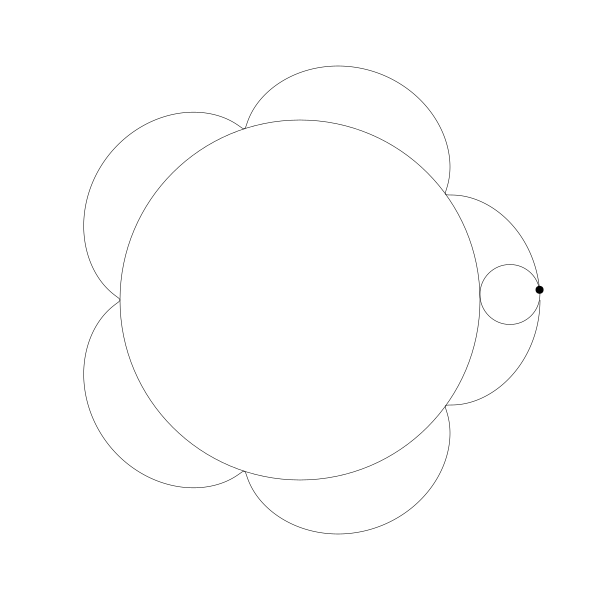
这就是你长短辐外摆线！

事实上，由于那个点是在圆周位置上，所以这也就是外摆线！

如果将点往外移动一点...

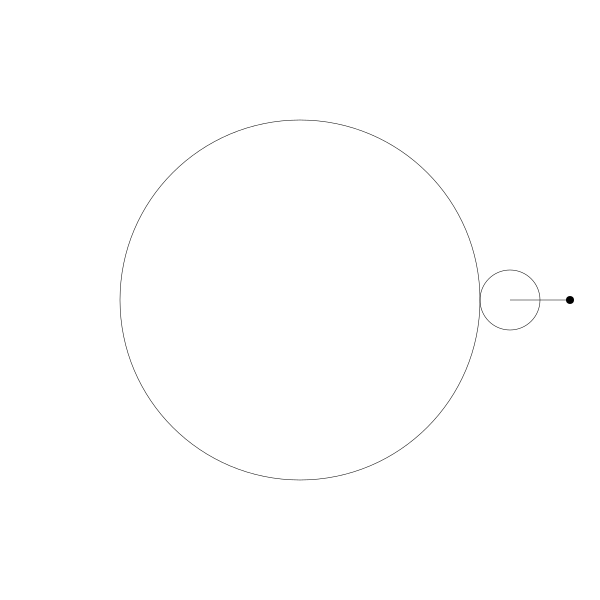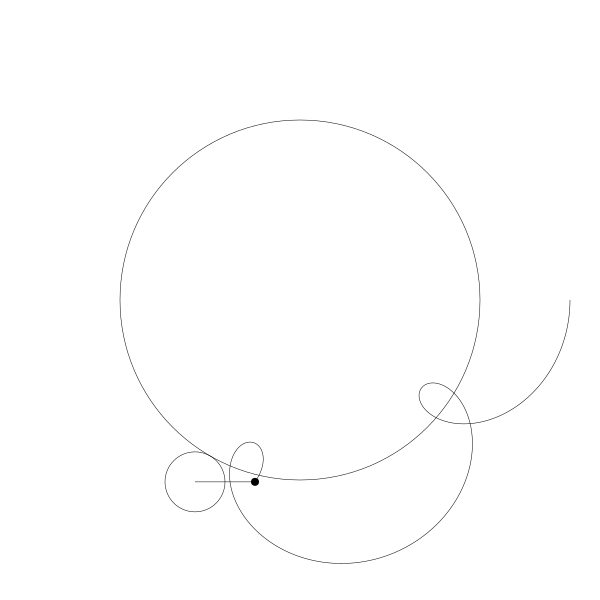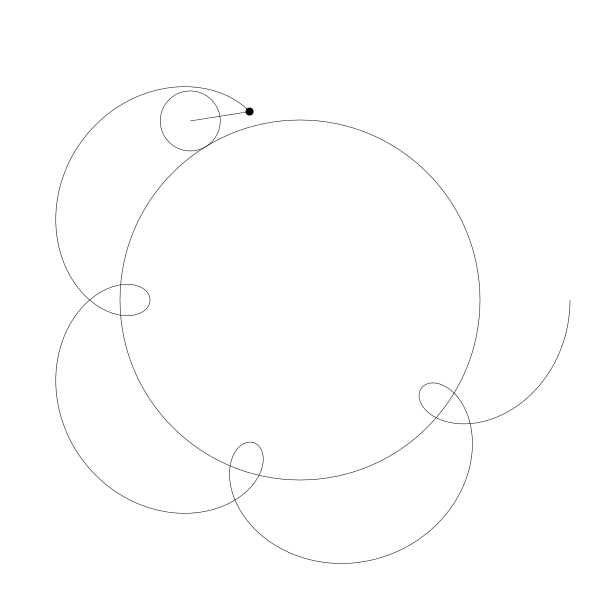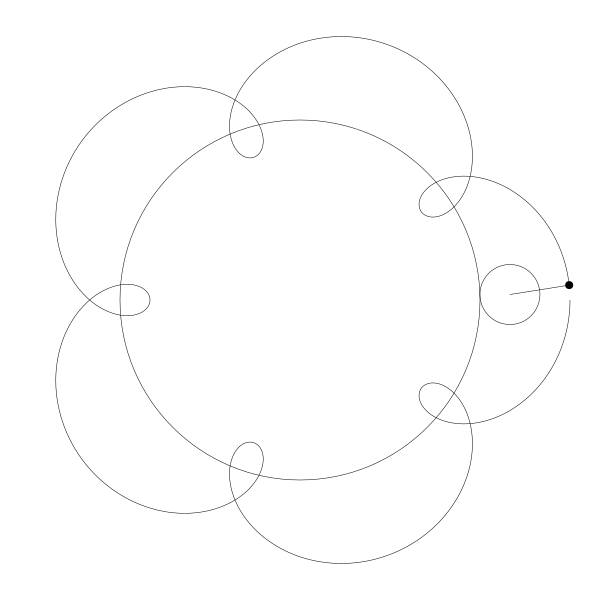
再我们往内移动一点。

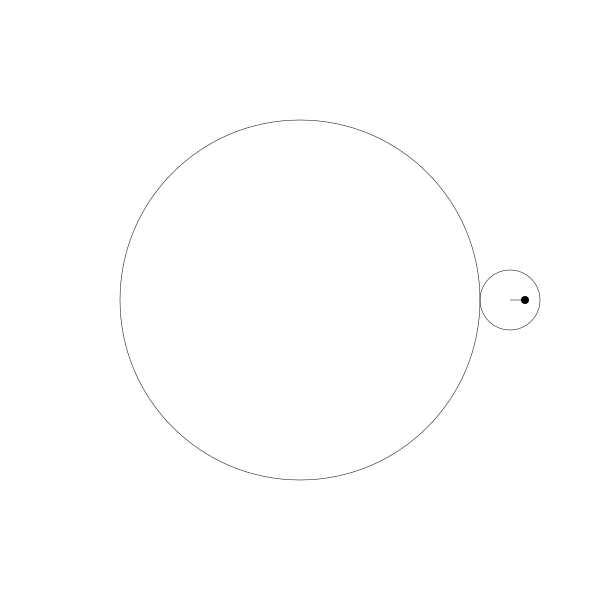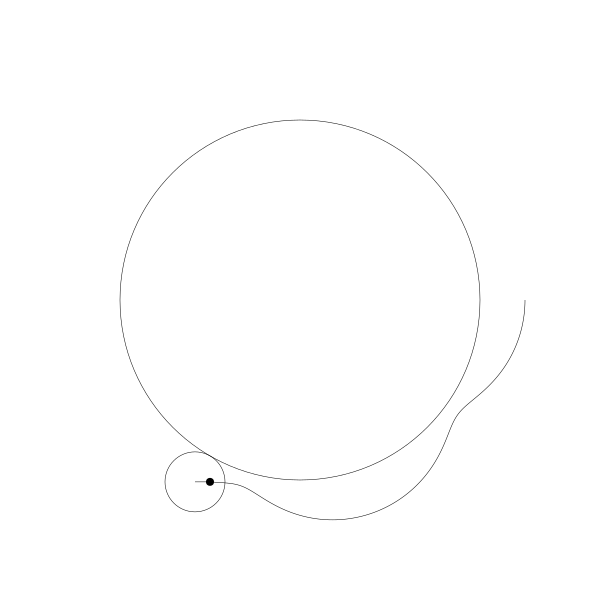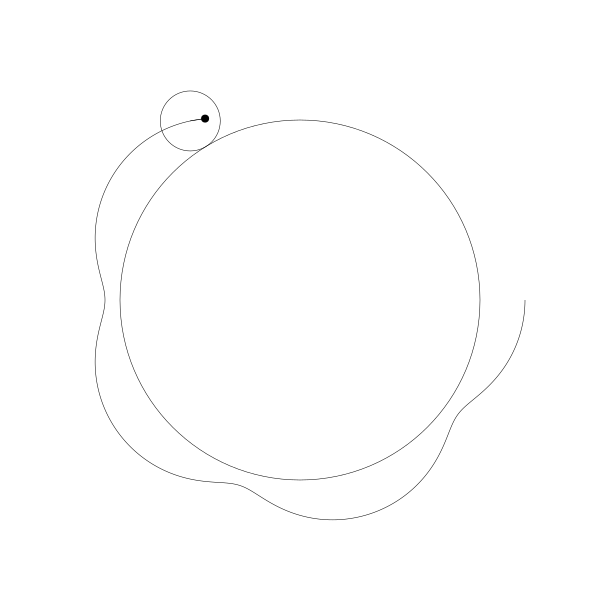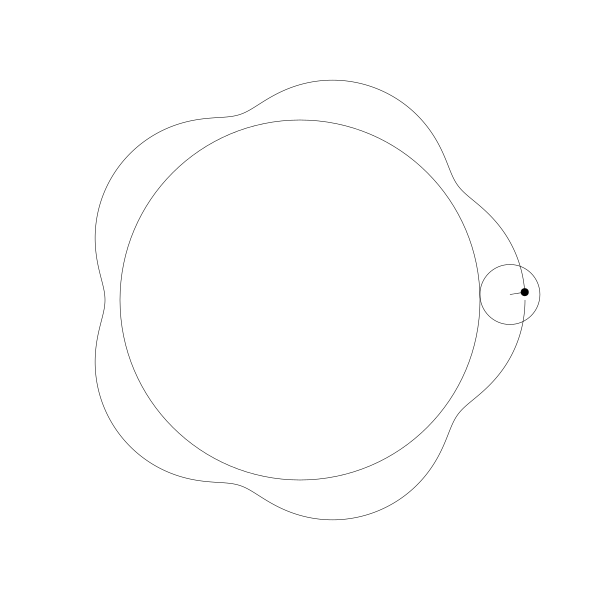
再一次，我创建这些动画是通过计算这些圆的位置，绘制这些圆，再计算这些圆的旋转角度并绘制对应的点， 然后再连接每一帧所绘制的点路径形成曲线。为了展示动画像这么做是值得的，但是其实是有更简单的公式，你可以直接应用：

长短辐外摆线公式：

x = (r0 + r1) * cos(t) - d * cos(((r0 + r1) * t) / r1)
y = (r0 + r1) * sin(t) - d * sin(((r0 + r1) * t) / r1)

参数解析：

• r0 是定圆的半径
• r1 是动圆的半径
• t 是增长的弧度
• d 是动圆中心点与绘制点之间的距离 (如果是外摆线则 r1 与 d 相同)

我们用这个公式瞬间就可以用些代码实现：

width = 800
height = 800
canvas(width, height)

translate(width/2, height/2)

r0 = 180
r1 = 60
d = 60
res = 0.01

circle(0, 0, r0)
stroke()

for (t = 0.0; t < PI * 2; t += res) {
  x = (r0 + r1) * cos(t) - d * cos(((r0 + r1) * t) / r1)
  y = (r0 + r1) * sin(t) - d * sin(((r0 + r1) * t) / r1)
  lineTo(x, y)
}
stroke()

我们设置变量 r0, r1, d 然后绘制定圆仅仅是为了引用变量

接着循环 t 至 2 * PI, 得到 x， y 点，绘制一条线至那个点。

得到结果：

值得注意的一点， ro 到 r1 的比例。 180:60 或 3:1。 我们得到3个结点。如果将 r1 改为 45，比例即变为 4:1 ， 我们将得到 4 个结点。（我将 d 变为 45 也是为了适配 r1）

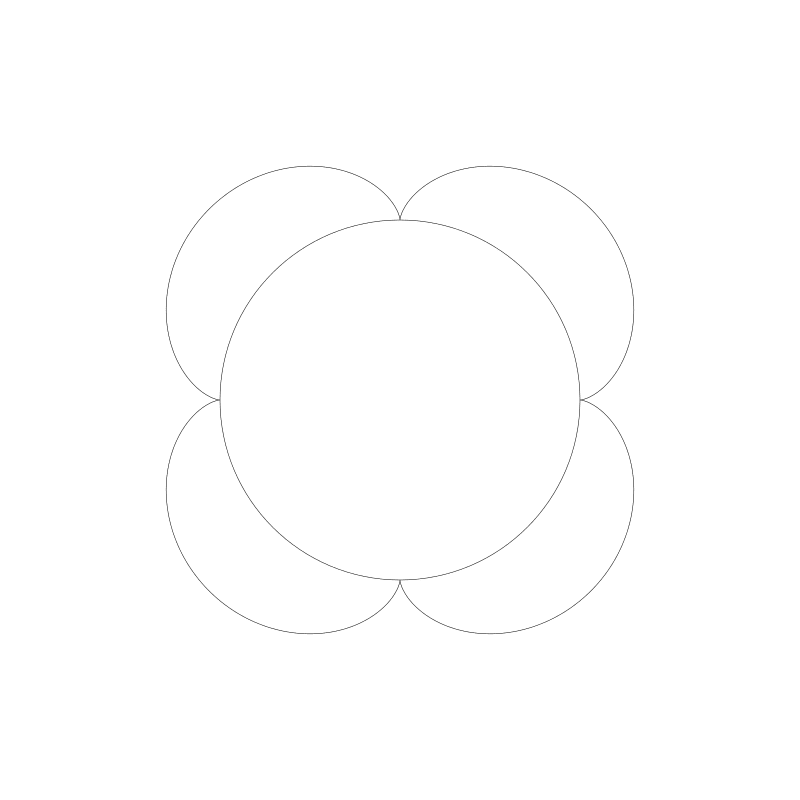
下面是 12:1 :

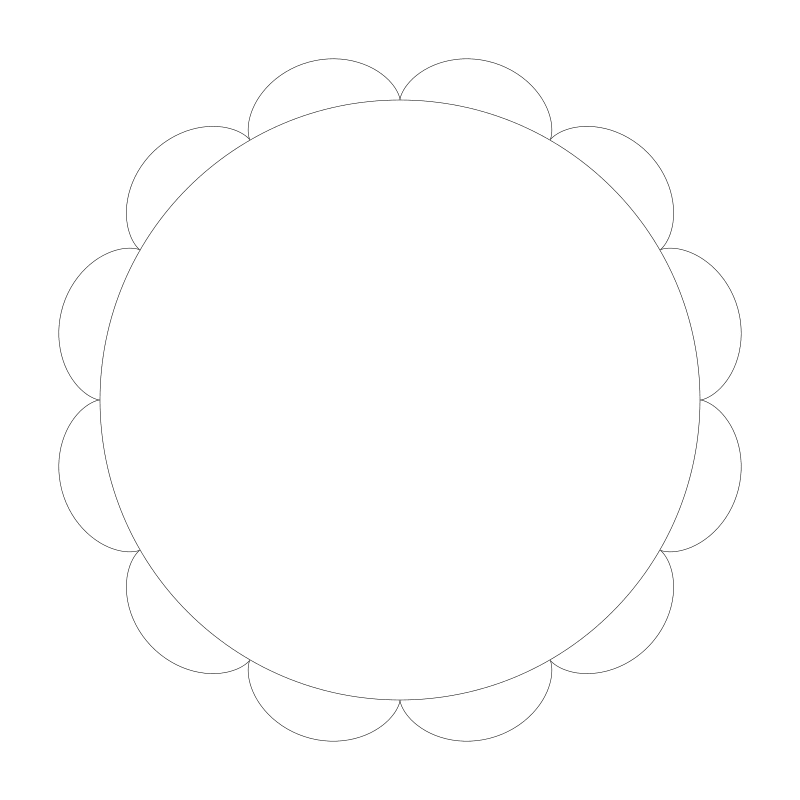
如果比例的第二个数字不是1，会如何？让我们将 r0 设置为 150，r1 为 100。现在，ratio 为 3:2。

毫无意外，我们得到了一个半的结点（nodes）。为了完成这个曲线，我们不得不再绕一圈，需要将 t 的范围值变为 0 到 PI * 4。然后得到结果：

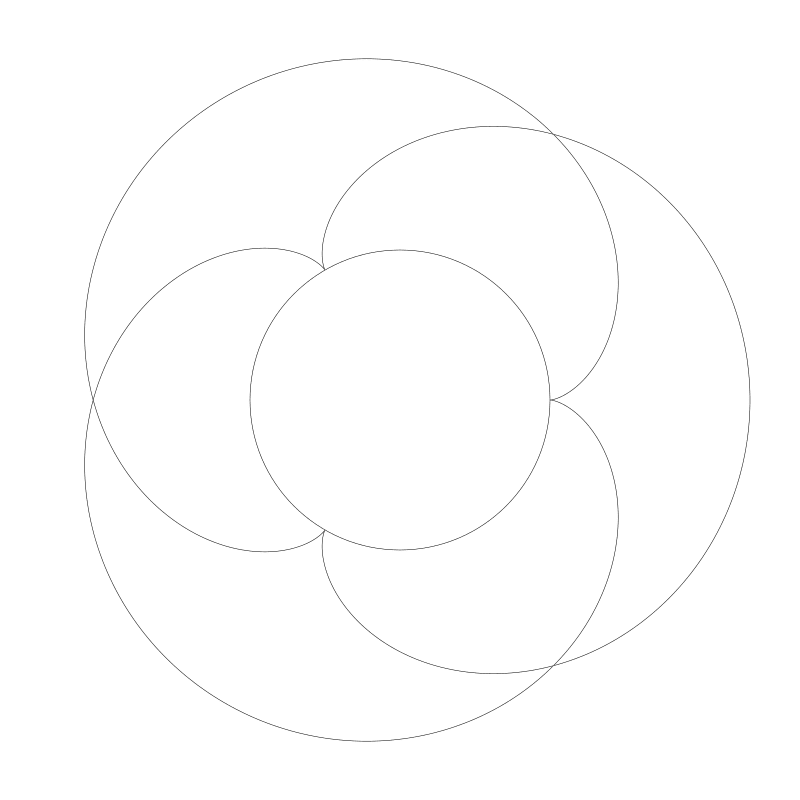
如果你使用整数，循环总是会完成的。在下一个例子中，比如是 11:7 ，所以不得不将 t 结束值调整为 PI * 14：

如果是 111:70， 意味着我需要 t 结束范围调整至 140 * PI:

手动算这个有点痛苦，你可以创建个函数简化比例计算并用分母 * PI * 2 作为循环次数。 下面有两个有用的函数

//（译者注： gcd 即 greatest common divisor 求最大公约数）
function gcd(x, y) {
  result min(x, y)
  while (result > 0) {
    if (x % result == 0 && y % result == 0) {
      break
    }
    result--
  }
  return result
}

function simplify(x, y) {
  g = gcd(x, y)
  return x / g, y / g
}

仅需要将 r0 和 r1 传入 simplify 函数，得到简化后的比例。将结果的第二个数字 * 2 * PI 做为循环的结束条件。下面是例子...

（译得注：简化比例式，最后将分母 * 2 * PI）

width = 800
height = 800
canvas(width, height)

translate(width/2, height/2)

r0 = 111
r1 = 70
d = 70
res = 0.01
num, den = simplify(r0, r1)

circle(0, 0, r0)
stroke()

for (t = 0.0; t < PI * 2 * den; t += res) {
  x = (r0 + r1) * cos(t) - d * cos(((r0 + r1) * t) / r1)
  y = (r0 + r1) * sin(t) - d * sin(((r0 + r1) * t) / r1)
  lineTo(x, y)
}
stroke()

用化简后的分数的分母保证循环足够多闪以形成完整的曲线。

到目前为止，全部是外摆线(圆外旋轮线)。 让我们改变参数 d 来创建一些其它的长短幅外摆线。

让 d 大于 r1:

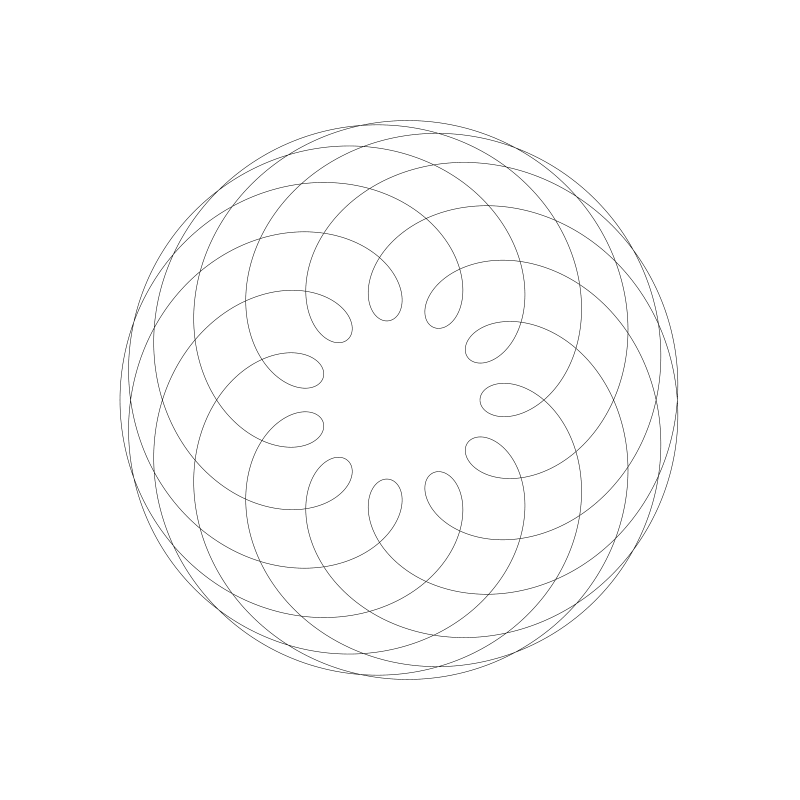
d 小于 r1:

在这些例子中我没有再把内圆画出来。

你无需让我再提供更多的例子了。只需要改变数字看看能得到啥结果。

特殊长短幅外摆线

蚶线是长短幅摆线的一种，生成它的两个圆半径相等。如果两个点在圆内，则它是特殊的蚶线被称为 Cardioid 心形曲线。

下面是一个蚶线，两个半径都是 80 ， d 值设为 160。

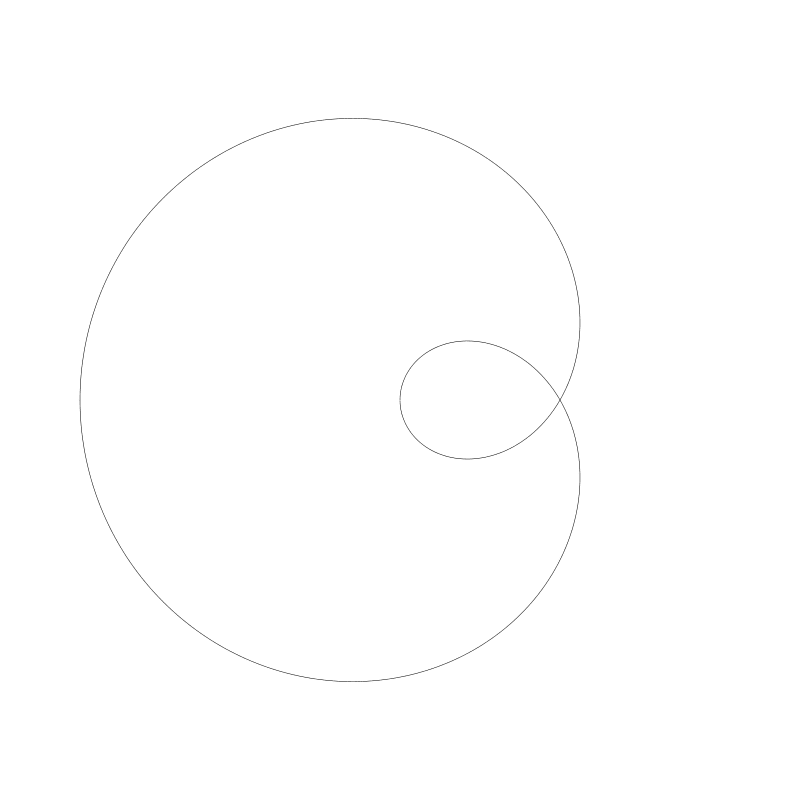
心形线三个值都设为 80

肾脏线是长短幅外摆线的一类，它的定圆半径是动圆半径的2倍，且那个点在动圆的圆周上。这是肾脏线的图

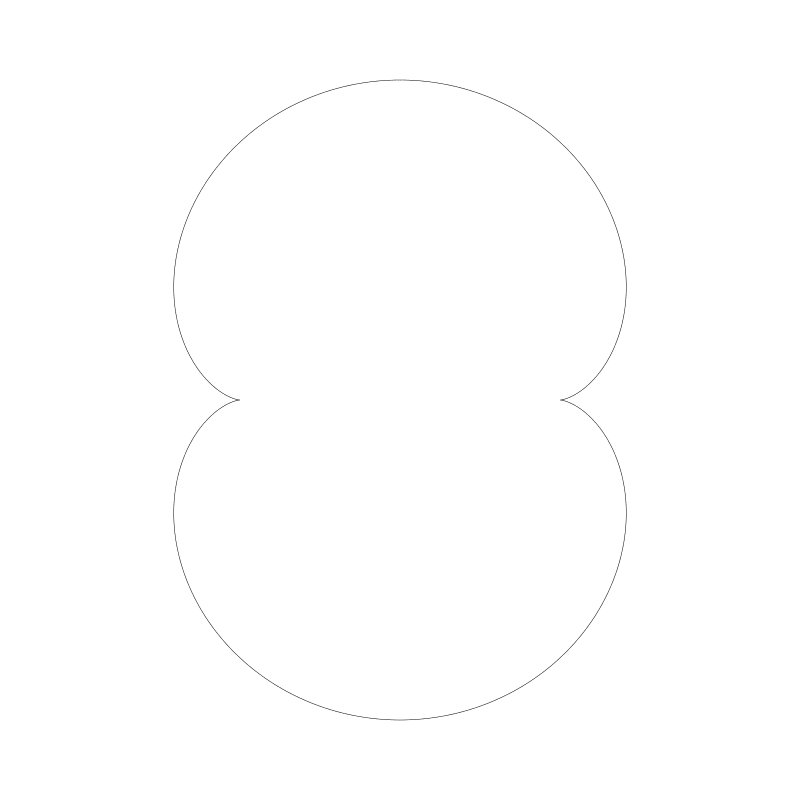
你也可以让那个动圆上的点不在动圆圆周上，但却不再是肾脏线了，但依然是很不错的曲线。

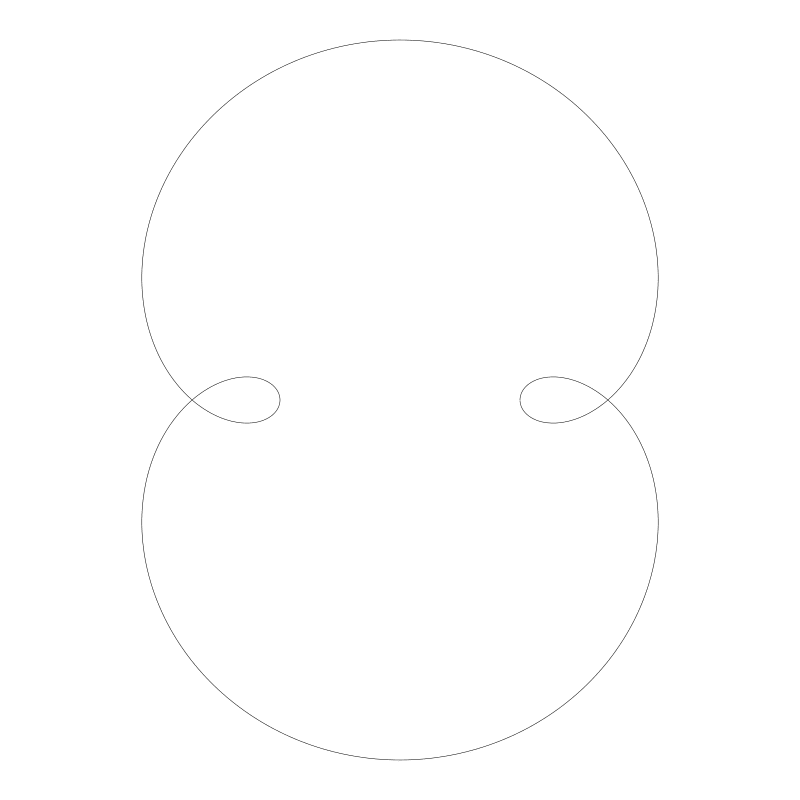
现在让我们把视线转向长短幅内摆线！

长短幅内摆线

正如前面提到的，长短幅内摆线其实就是动圆是延定圆内部滚动的。

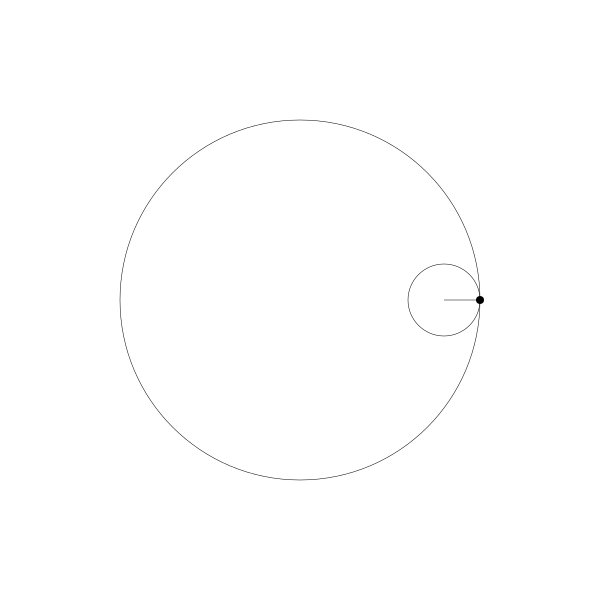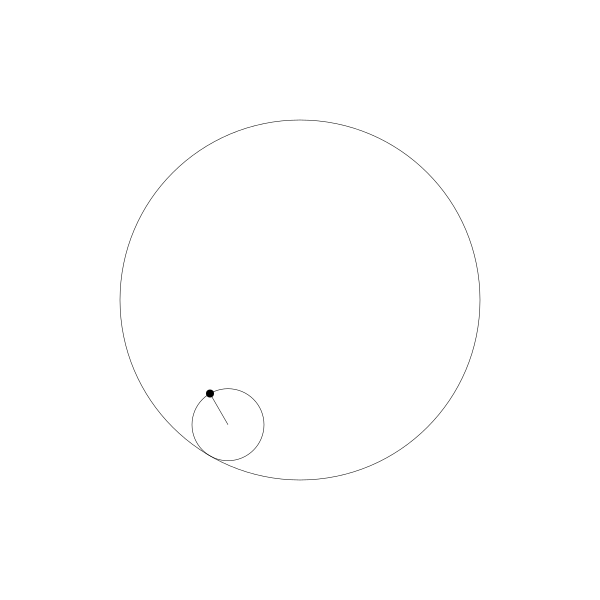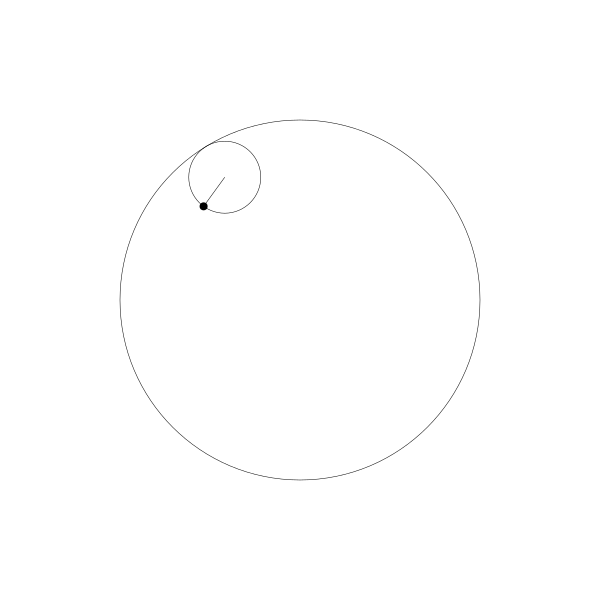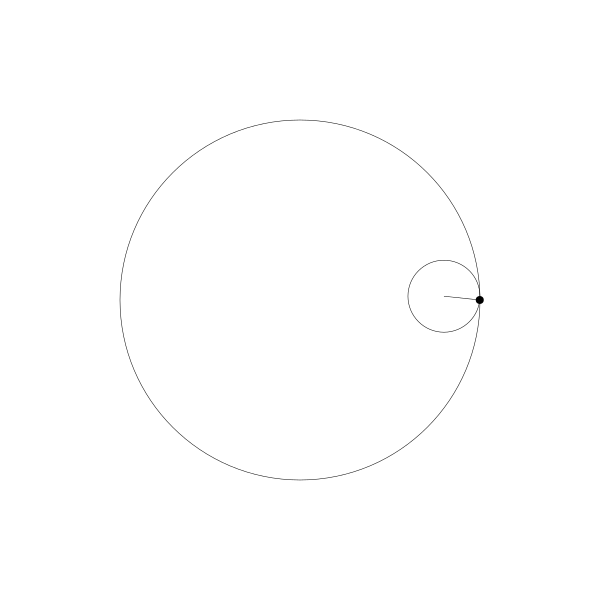
我们跟踪那个曲线上的绘制点，就得到了长短幅内摆线

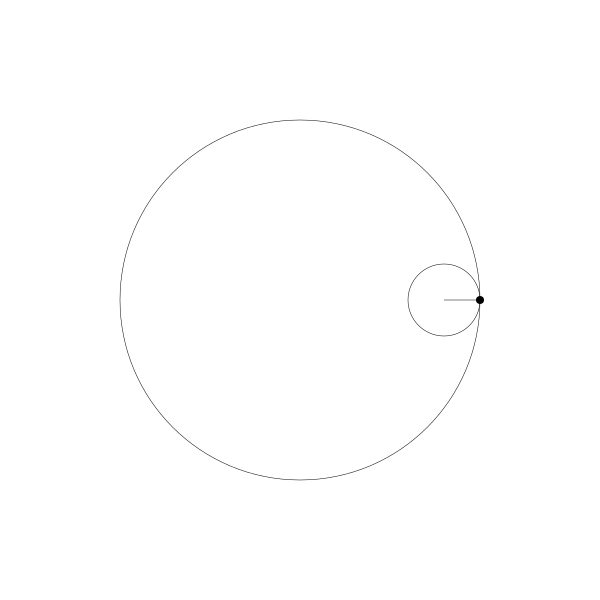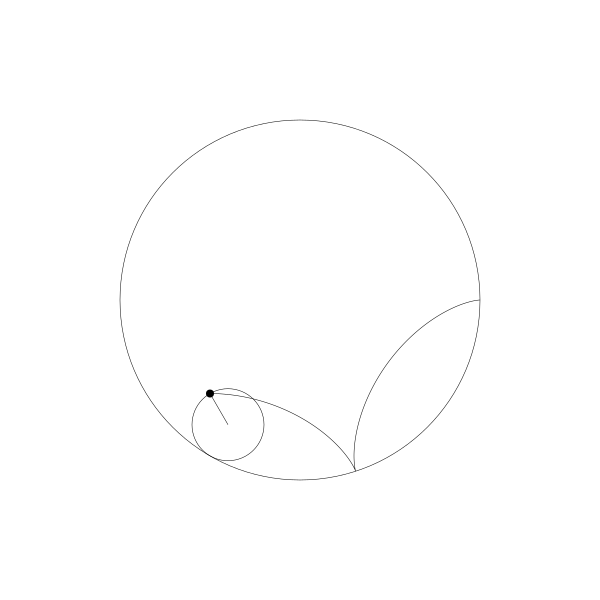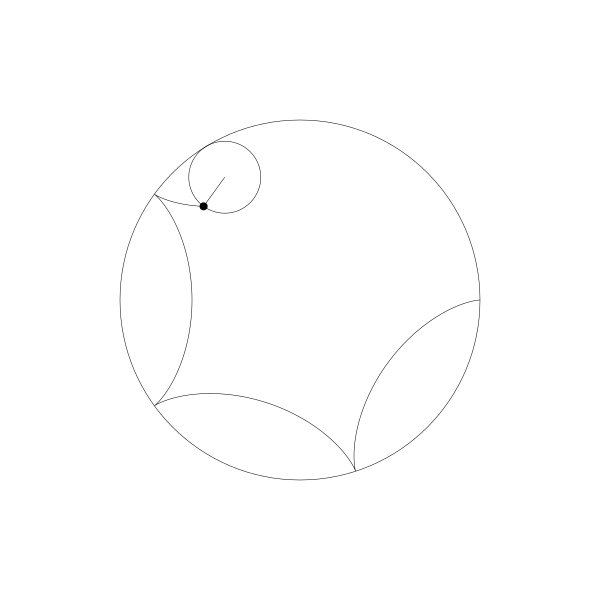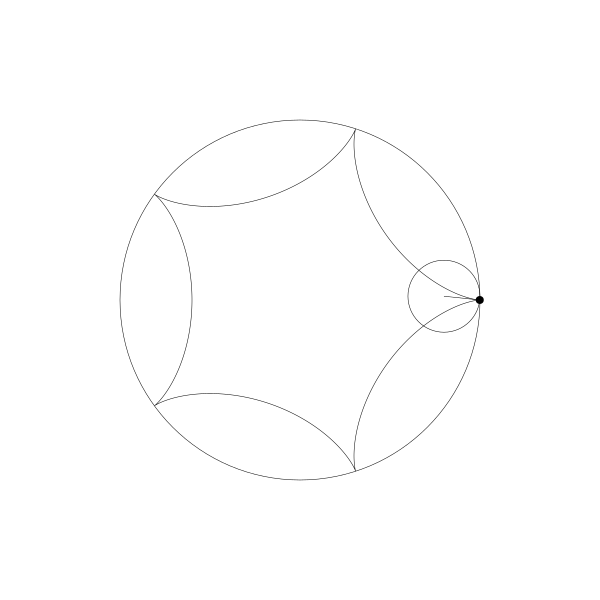
事实上，由于绘制点在动圆圆周上，它就是内摆线。

当绘制点移动到动圆外部， 得到的就是：

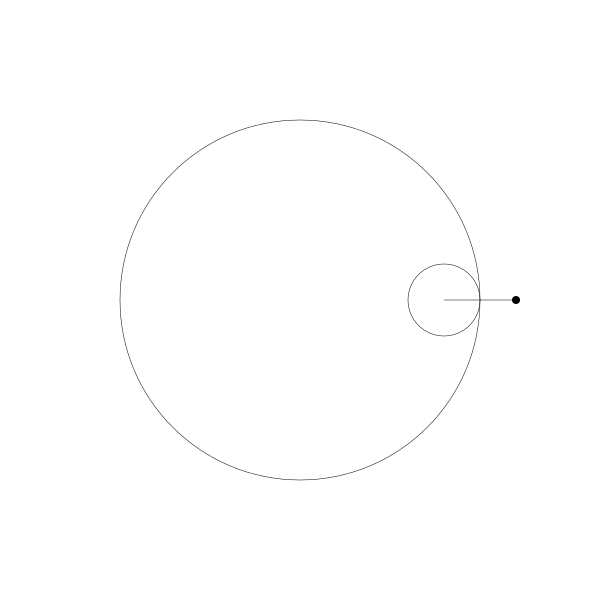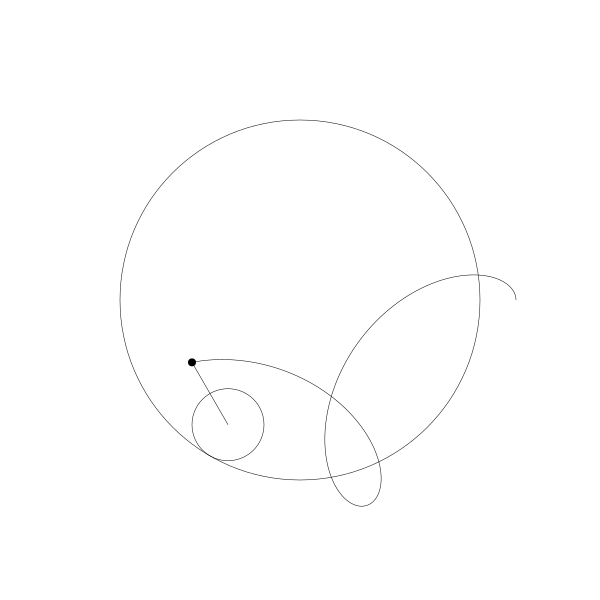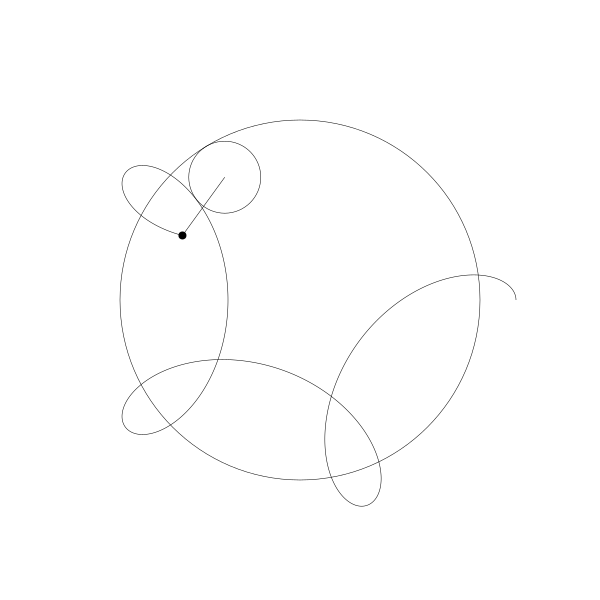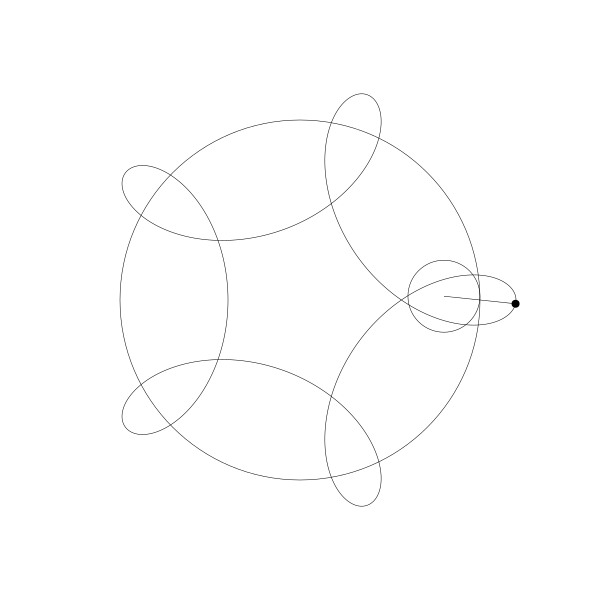
当绘制点移到动圆内部...

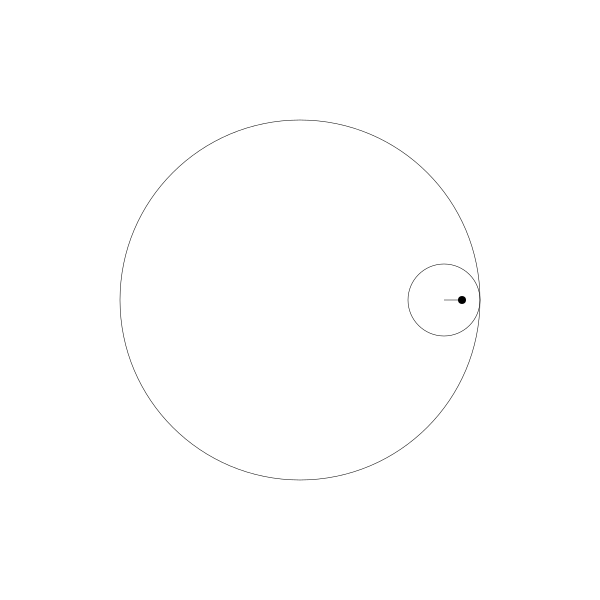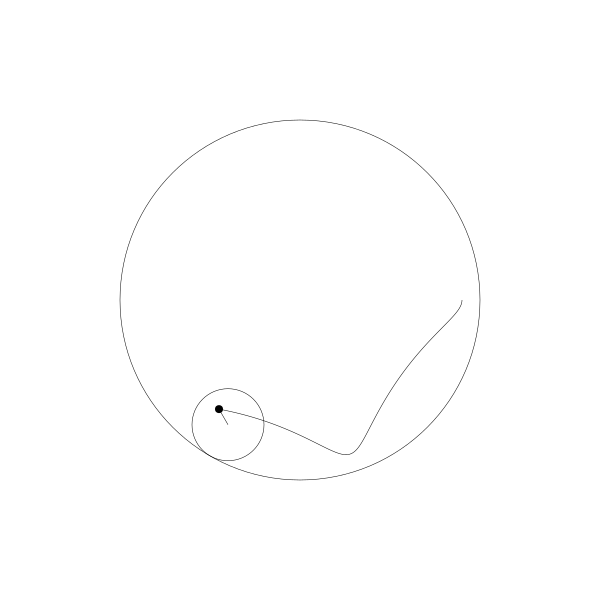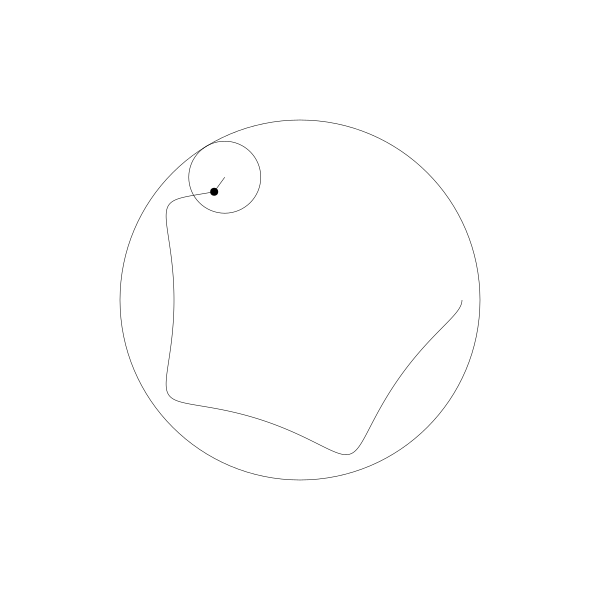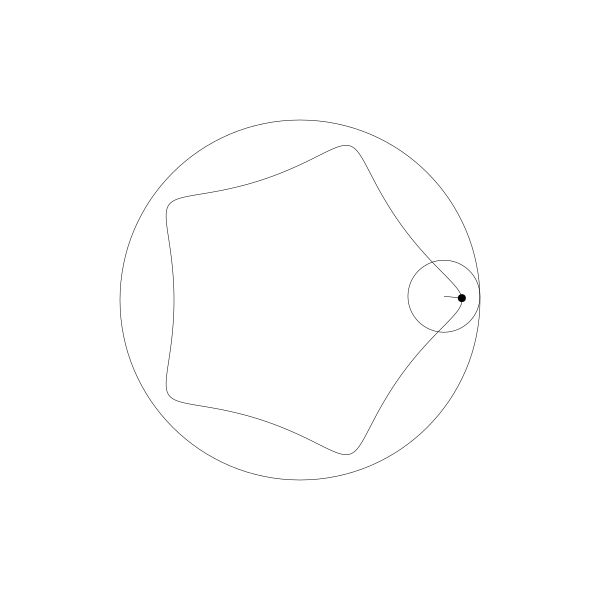
像之前一样，这个动画是用野路子创建的，其实是有简单公式可以实现。

长短幅内摆线公式：

x = (r0 - r1) * cos(t) + d * cos(((r0 - r1) * t) / r1)
y = (r0 - r1) * sin(t) - d * sin(((r0 - r1) * t) / r1)

参数与长短幅外摆线类似，事实上公式也基本相同，仅有几项符号不同。

下面是使用方法。

width = 800
height = 800
canvas(width, height)

translate(width/2, height/2)

r0 = 300
r1 = 50
d = 50
res = 0.01
num, den = simplify(r0, r1)

for (t = 0.0; t < PI * 2 * den; t += res) {
  x = (r0 - r1) * cos(t) + d * cos(((r0 - r1) * t) / r1)
  y = (r0 - r1) * sin(t) - d * sin(((r0 - r1) * t) / r1)
}
stroke()

代码运行结果：

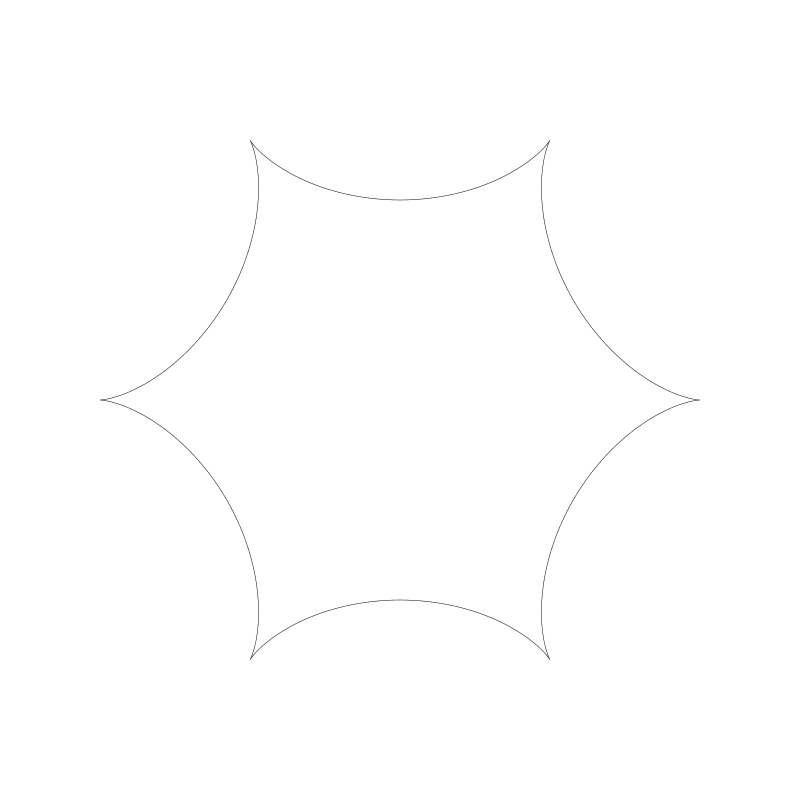
注意 r0 与 r1 比例是 6:1, 拥有 6 个点。比例的作用原理与之前的长短幅外摆线一样

下面是半径 312 和 76 (译者注：这里 r0 为 312，r1，d 都为 76)：

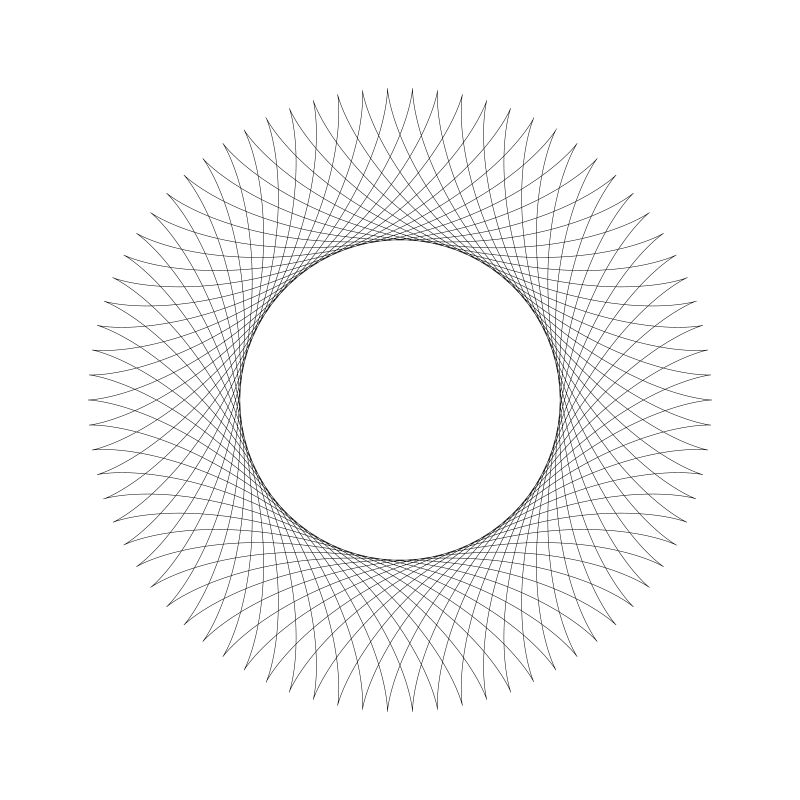
将绘制点 d 值设大一点移出动圆圆周：

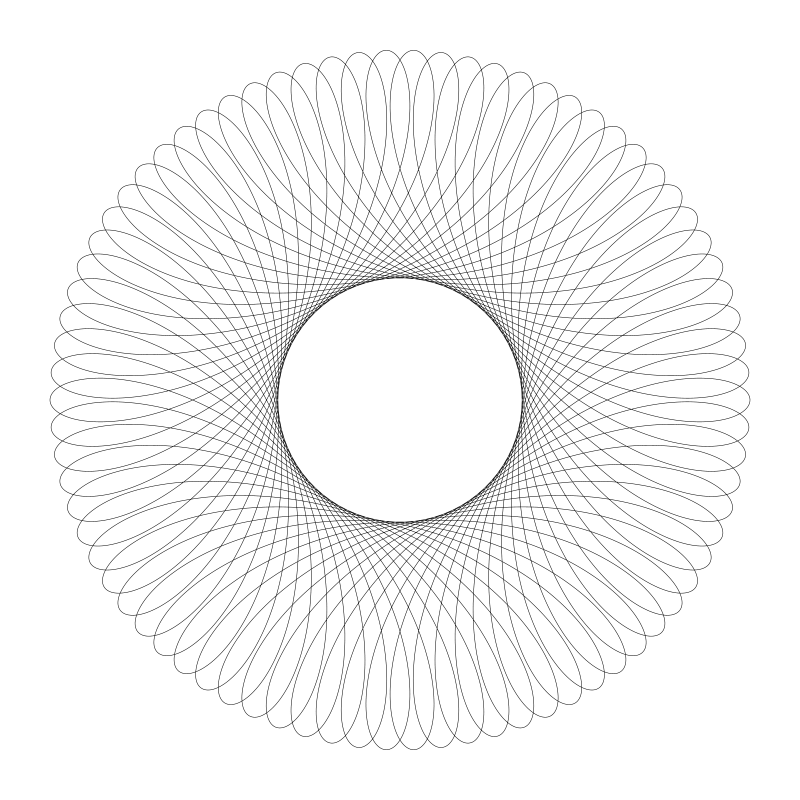
移入动圆内...

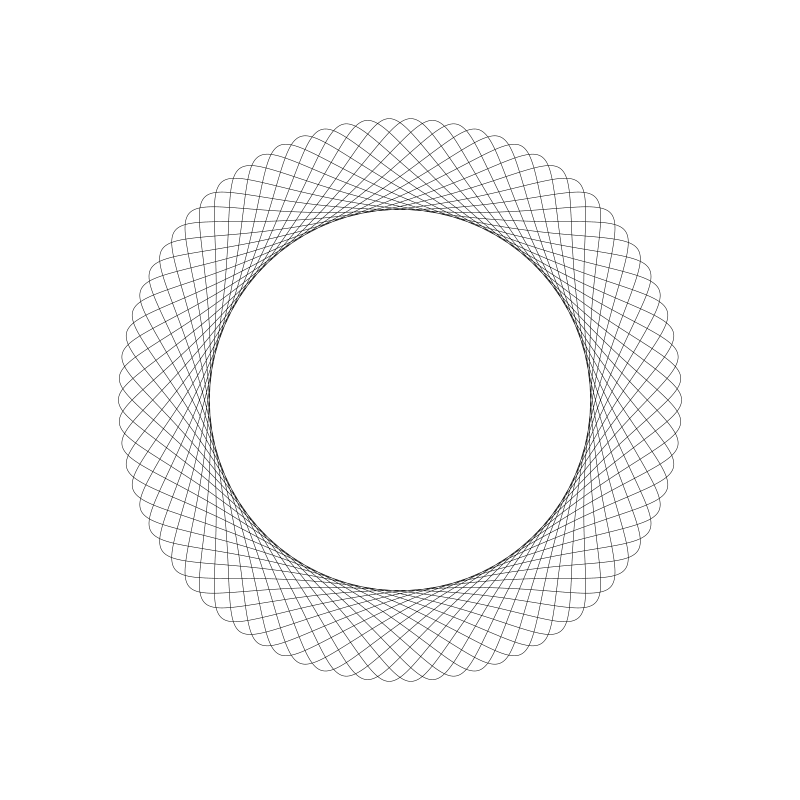
如果你不断尝试，我保证你能发掘出更多有趣的图形。

特殊长短幅内摆线

我将再介绍两种特殊长短幅内摆线。我们需要再次调整两个圆的大小比例。

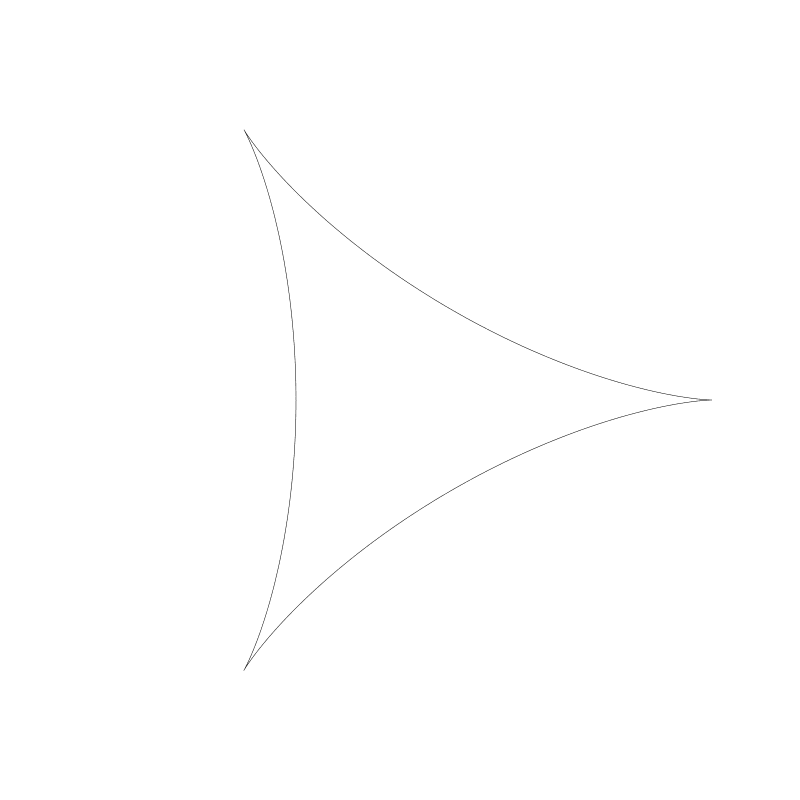
这是星状图的比例 4:1

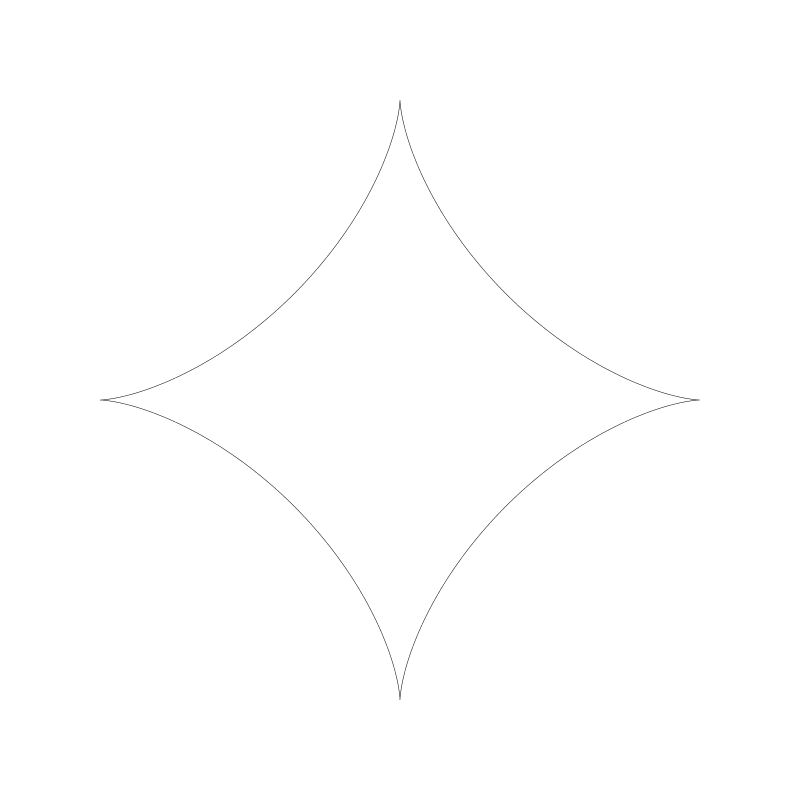
还有一个更有趣的比例 2:1. 被称为图斯双圆，以描述它的13世纪波斯天文学家名字而命名。下面是演示它的动画。

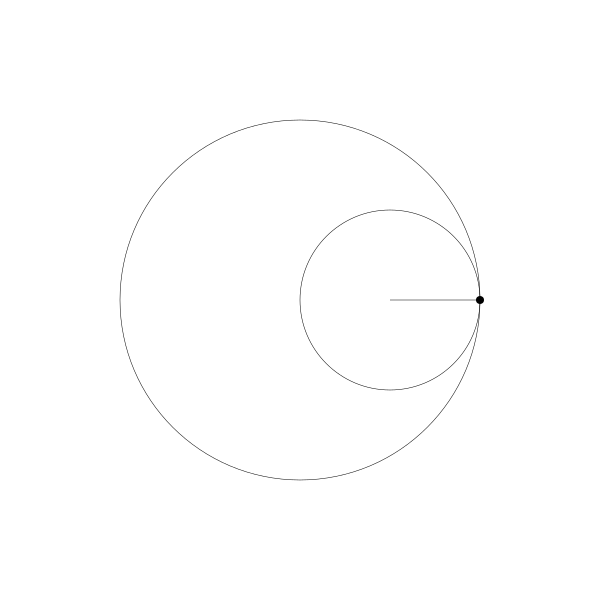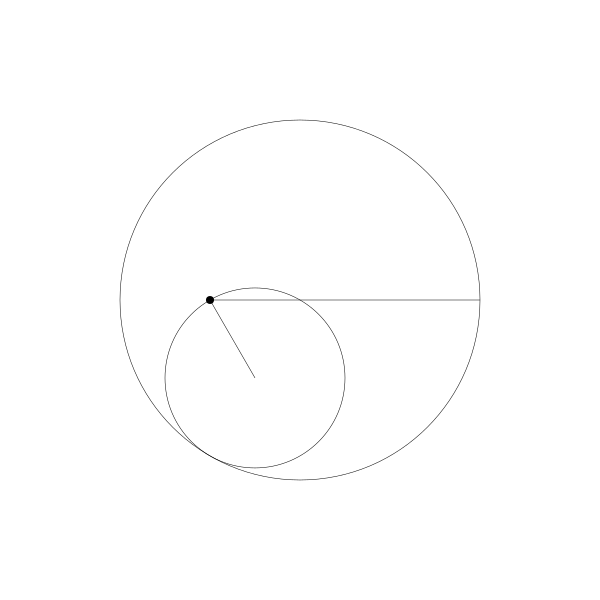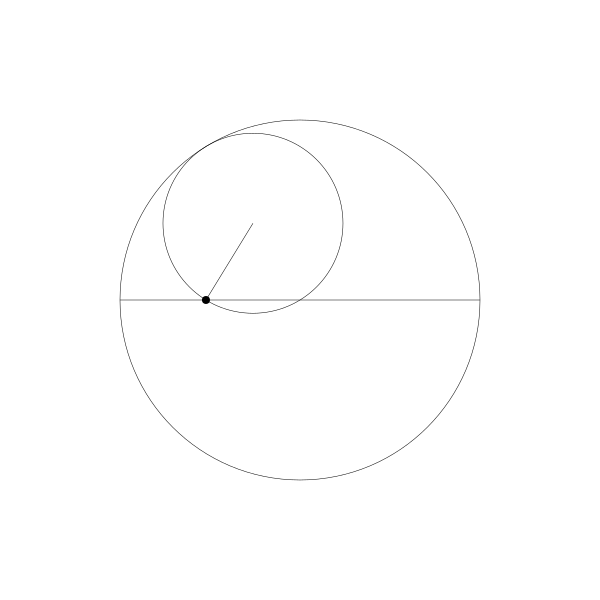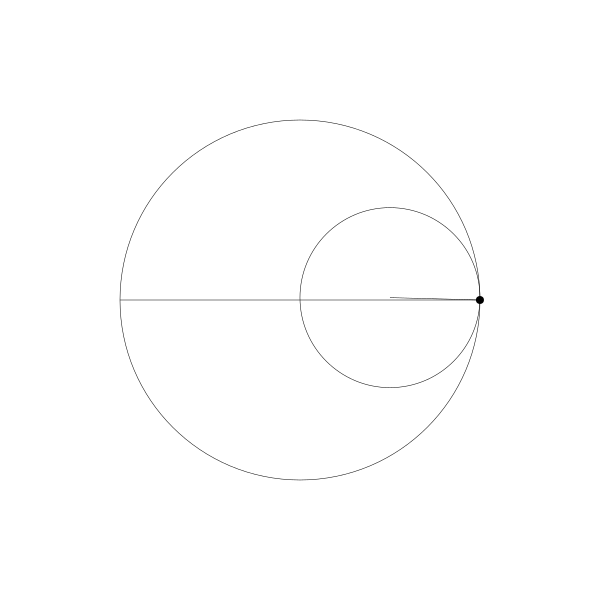
正如你所看到的，形成了一条直线。

如果你多创建几个动圆，并将每个动圆的绘制点相位与前一个相比再往后调整一点，你将会得到如下图：

每个点延直线来回运动。如果你将所有线条和动圆移除，你会得到一个旋转的圆的错觉。事实上，它看起来像是另一个内摆线

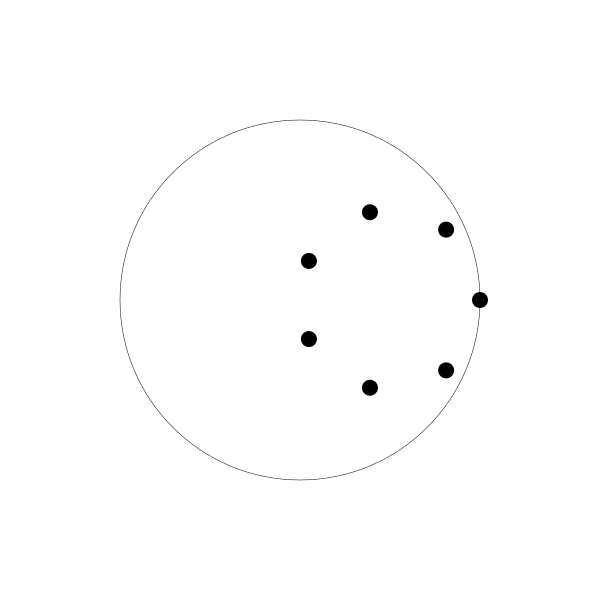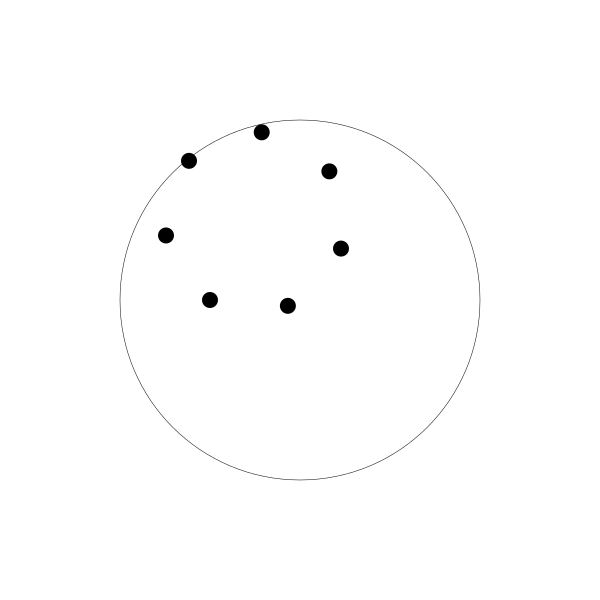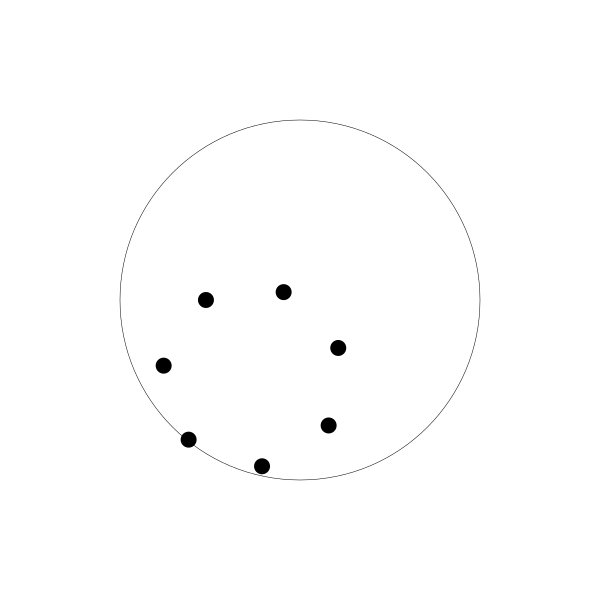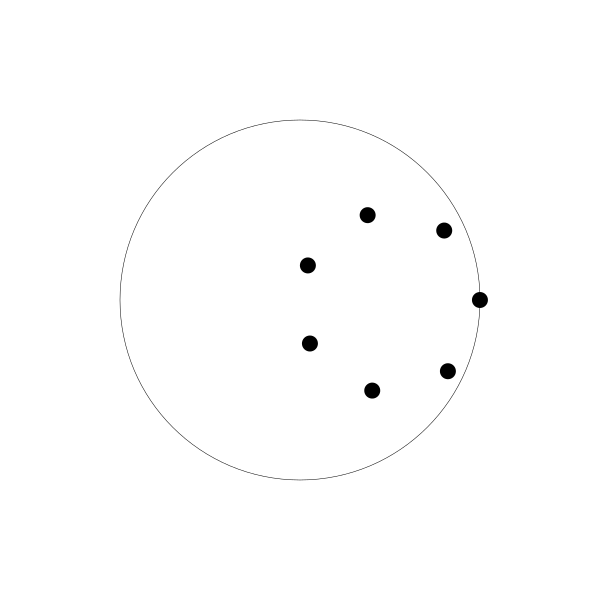
螺旋图！

小时候如果你像我一样比较呆，那么你可能也会像我这样拥有下面这些东西（译者注：可能我不够呆，反正我没有过，倒是见过同学有类似的东西--!）：

这是几个星期前为写这一章内容我新买的。它很酷，锡盒子包装内包含了一些绘制用的纸还有使用说明和灵感小册子。

大的齿轮固定在纸上。过去用的是小钉子，现在用的是用粘粘的东西（sticky-tack 多伟大的改进！）固定住，还有一些小的多孔的小齿轮。你将笔插进这些小孔中，让它延着大圆旋转一圈。

瞧！一个长短幅内摆线

如果你将小齿轮摆外面滚一轮，它就是长短幅外摆线。相当有趣，说实施，我还是更喜欢用代码实现它。下面是绘制过程中笔滑了，这让线条看起来有点儿乱。笔触也断断续续的。

当我玩的过程中才发现，它只能画出短幅摆线和内摆线。绘制点只能是在移动的齿轮内。

本章 Javascript 源码 https://github.com/willian12345/coding-curves/blob/main/examples/ch09

---

博客园: http://cnblogs.com/willian/

github: https://github.com/willian12345/