POJ1743 Musical Theme —— 后缀数组 重复出现且不重叠的最长子串

题目链接：https://vjudge.net/problem/POJ-1743

Musical Theme

Time Limit: 1000MS		Memory Limit: 30000K
Total Submissions: 32402		Accepted: 10808

Description

A musical melody is represented as a sequence of N (1<=N<=20000)notes that are integers in the range 1..88, each representing a key on the piano. It is unfortunate but true that this representation of melodies ignores the notion of musical timing; but, this programming task is about notes and not timings. 
Many composers structure their music around a repeating &qout;theme&qout;, which, being a subsequence of an entire melody, is a sequence of integers in our representation. A subsequence of a melody is a theme if it:

• is at least five notes long
• appears (potentially transposed -- see below) again somewhere else in the piece of music
• is disjoint from (i.e., non-overlapping with) at least one of its other appearance(s)

Transposed means that a constant positive or negative value is added to every note value in the theme subsequence. 
Given a melody, compute the length (number of notes) of the longest theme. 
One second time limit for this problem's solutions! 

Input

The input contains several test cases. The first line of each test case contains the integer N. The following n integers represent the sequence of notes. 
The last test case is followed by one zero. 

Output

For each test case, the output file should contain a single line with a single integer that represents the length of the longest theme. If there are no themes, output 0.

Sample Input

30
25 27 30 34 39 45 52 60 69 79 69 60 52 45 39 34 30 26 22 18
82 78 74 70 66 67 64 60 65 80
0

Sample Output

5

Hint

Use scanf instead of cin to reduce the read time.

Source

LouTiancheng@POJ

题意：

给出一串数字，定义theme为：长度不小于5，从左到右以相同的变化规律出现了不止一次，并且不能重叠。求最长的theme。实际上是求：字符串的重复出现且不重叠的最长子串。

题解：

1.由于求的是变化规律，所以要求出相邻两个数的差值，得到新的一串数字。然后求出新串的后缀数组。

2.二分答案，即“重复出现且不重叠的最长子串”的长度k。然后根据是否存在这样的子串来缩小k的范围，最终得到答案。那么怎样判断是否存在“重复出现且不重叠的长度为k的子串”呢？

2.1 把后缀按名次排成一列，如果前m个后缀（第一名除外）与它的前一名的最长公共前缀都大于等于k（二分时的mid），即height[2~m]>=k，则可以说明这m个后缀的最长公共前缀大于等于k。所以可以得出结论：k把所有后缀分成若干组，并且每一组的最长公共前缀大于等于k（可以单独一个后缀作为一组）。那么，我们只需要判断：是否存在一组后缀，使得max(sa[i]) - min(sa[i]) >= k。

2.2 视图更加直观：

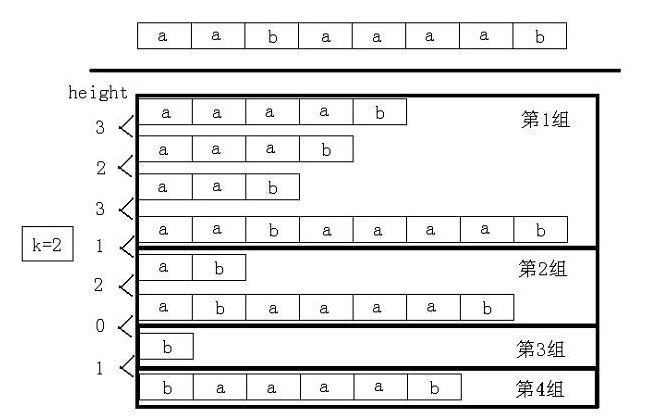
2.3 参考：http://blog.csdn.net/huangzhengdoc/article/details/53573198

代码如下：

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 #include <vector>
 #include <cmath>
 #include <queue>
 #include <stack>
 #include <map>
 #include <string>
 #include <set>
 using namespace std;
 typedef long long LL;
 const double EPS = 1e-;
 const int INF = 2e9;
 const LL LNF = 9e18;
 const int MOD = 1e5;
 const int MAXN = +;
 
 bool cmp(int *r, int a, int b, int l)
 {
     return r[a]==r[b] && r[a+l]==r[b+l];
 }
 
 int r[MAXN], sa[MAXN], Rank[MAXN], height[MAXN];
 int t1[MAXN], t2[MAXN], c[MAXN];
 void DA(int str[], int sa[], int Rank[], int height[], int n, int m)
 {
     n++;
     int i, j, p, *x = t1, *y = t2;
     for(i = ; i<m; i++) c[i] = ;
     for(i = ; i<n; i++) c[x[i] = str[i]]++;
     for(i = ; i<m; i++) c[i] += c[i-];
     for(i = n-; i>=; i--) sa[--c[x[i]]] = i;
     for(j = ; j<=n; j <<= )
     {
         p = ;
         for(i = n-j; i<n; i++) y[p++] = i;
         for(i = ; i<n; i++) if(sa[i]>=j) y[p++] = sa[i]-j;
 
         for(i = ; i<m; i++) c[i] = ;
         for(i = ; i<n; i++) c[x[y[i]]]++;
         for(i = ; i<m; i++) c[i] += c[i-];
         for(i = n-; i>=; i--) sa[--c[x[y[i]]]] = y[i];
 
         swap(x, y);
         p = ; x[sa[]] = ;
         for(i = ; i<n; i++)
             x[sa[i]] = cmp(y, sa[i-], sa[i], j)?p-:p++;
         if(p>=n) break;
         m = p;
     }
 
     int k = ;
     n--;
     for(i = ; i<=n; i++) Rank[sa[i]] = i;
     for(i = ; i<n; i++)
     {
         if(k) k--;
         j = sa[Rank[i]-];
         while(str[i+k]==str[j+k]) k++;
         height[Rank[i]] = k;
     }
 }
 
 bool test(int mid, int n)
 {
     int minn = sa[], maxx = sa[];
     for(int i = ; i<=n; i++)
     {
         if(height[i]<mid)
             minn = maxx = sa[i];
         else
         {
             maxx = max(maxx, sa[i]);
             minn = min(minn, sa[i]);
             if(maxx-minn>=mid)
                 return true;
         }
     }
     return false;
 }
 
 int main()
 {
     int n;
     while(scanf("%d",&n)&&n)
     {
         for(int i = ; i<n; i++) scanf("%d", &r[i]);
         for(int i = ; i<n-; i++) r[i] = r[i+]-r[i]+;
         r[--n] = ;
         DA(r, sa, Rank, height, n, );
         int l = , r = n/;
         while(l<=r)
         {
             int mid = (l+r)>>;
             if(test(mid, n))
                 l = mid + ;
             else
                 r = mid - ;
         }
         if(r<) printf("0\n");
         else printf("%d\n", r+);
     }
 }