洛谷——P1187 3D模型

P1187 3D模型

题目描述

一座城市建立在规则的n×m网格上，并且网格均由1×1正方形构成。在每个网格上都可以有一个建筑，建筑由若干个1×1×1的立方体搭建而成（也就是所有建筑的底部都在同一平面上的）。几个典型的城市模型如下图所示：

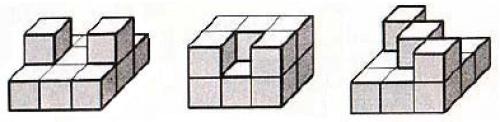
现在给出每个网格上建筑的高度，即每个网格上建筑由多少个立方体搭建而成，要求这个建筑模型的表面积是多少。

输入输出格式

输入格式：

输入文件的第1行包含2个正整数n和m，为城市模型的长与宽。

接下来n行，每行m个数字字符，描述了网格每个格子高度（可见所有建筑高度都大等于0且小等于9）。

输出格式：

输出文件包含一个非负整数，为城市模型的表面积。

输入输出样例

输入样例#1：

3 3
111
212
111

输出样例#1：

38

输入样例#2：

3 4
1000
0010
0000

输出样例#2：

12

说明

本题有2个测试数据

20%的数据满足：n, m≤10；

40%的数据满足：n, m≤100；

100%的数据满足：n, m≤1000。

很简单的一道模拟

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define N 1100
#define LL long long
using namespace std;
char ch;
LL n,m,tot,ans,a[N][N];
LL read()
{
    LL x=,f=; char ch=getchar();
    ') ch=getchar();
    +ch-',ch=getchar();
    return x*f;
}
int main()
{
    n=read(),m=read();
    ;i<=n;i++)
     ;j<=m;j++)
      cin>>ch,a[i][j]=ch-',tot+=a[i][j];
    ans=tot*;
    ;i<=n;i++)
     ;j<=m;j++)
     {
         ) ans-=*(a[i][j]-);
         ][j]) ans-=*min(a[i-][j],a[i][j]);
         ]) ans-=*min(a[i][j-],a[i][j]);
     }
    printf("%lld",ans);
    ;
}