【强网杯2018】逆向hide

这是事后才做出来的，网上没有找到现成的writeup，所以在这里记录一下

UPX加壳，而且linux下upx -d无法解，也无法gdb/ida attach

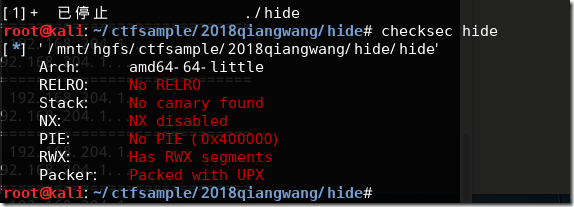
因为是64位，所以没有pushad，只能挨个函数进入，退出，看看程序是否恢复。

当运行到一0x400dd0，发现此时已经可以看见字符串了

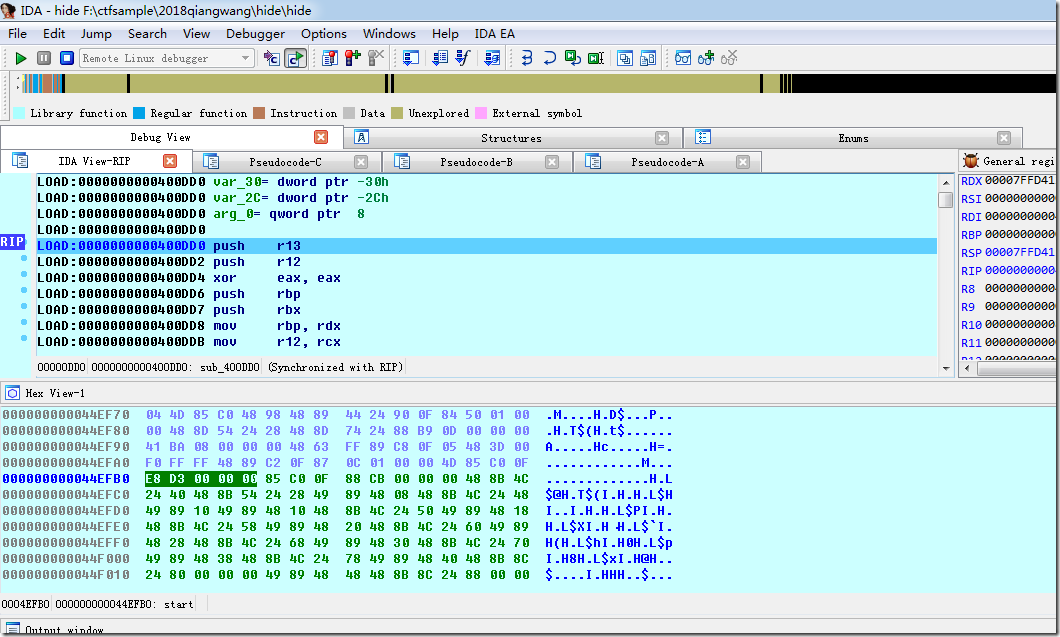
用dumphex的脚本来dump出内存，见hide_dump

static main(void)

{

auto fp, begin, end, dexbyte;

fp = fopen("C:\\dump.dex", "wb");

begin = 0x400000;

end = 0xADC000;

for ( dexbyte = begin; dexbyte < end; dexbyte ++ )

fputc(Byte(dexbyte), fp);

}

此时dump出的内容已经有程序运行的字符串了，通过字符串反查，这里

0x400890才是真正的启动地址

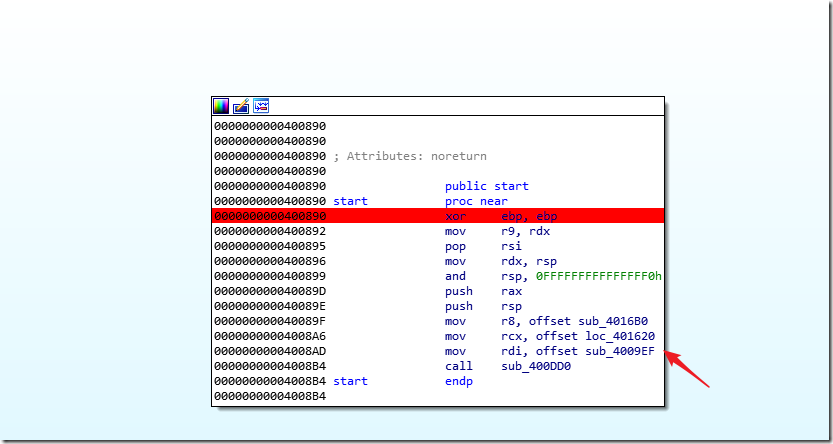
以后运行程序，在ida里面输入一下内容，即可直接运行到0x4009ef

from idaapi import *

from idc import *

run_to(0x4009ef)

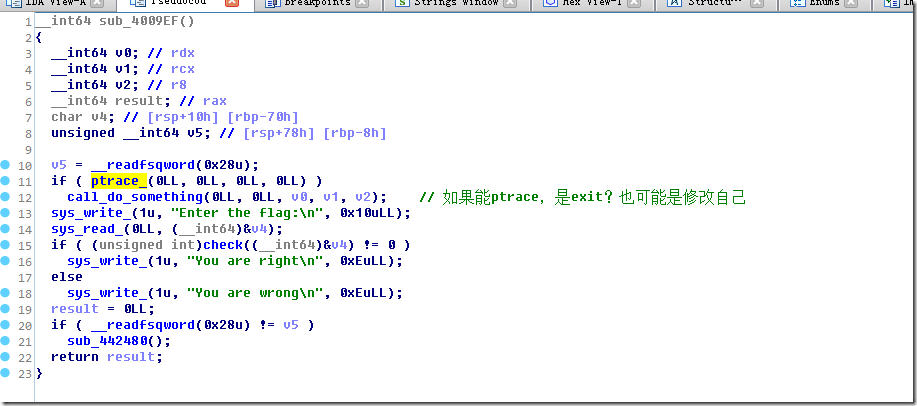
qwb{this_is_wrong_flag}

check到一个假flag，如果此时绕过ptrace且用ctrl+d作为结束，可以输出right。

但是输入到正常程序是报wrong的，说明还有地方反调试以及修改了逻辑

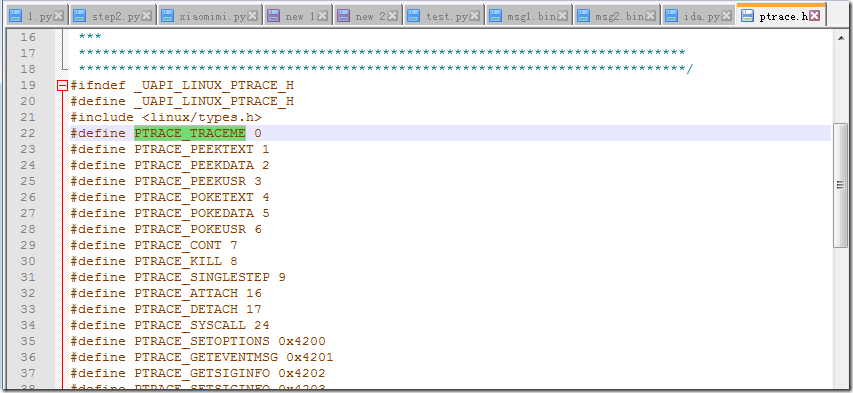
根据ptrace.h，ptrace这里是PTRACE_TRACEME，自我调试

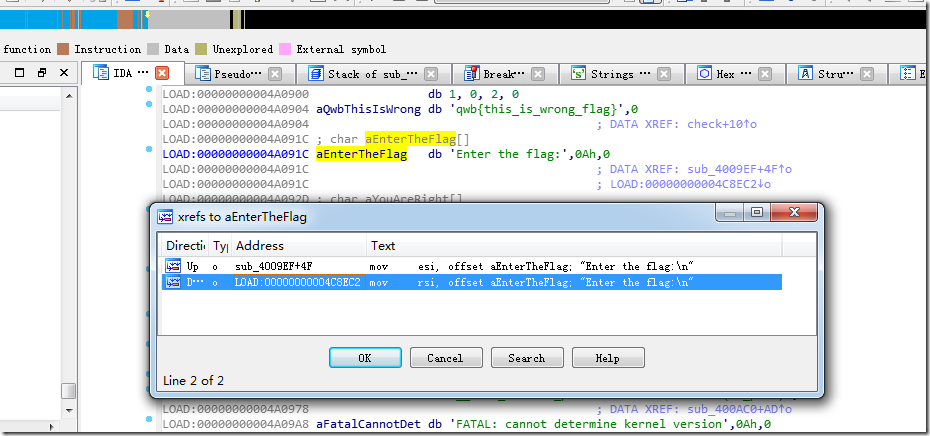
突然发现“Enter the flag:”字符串有2处引用

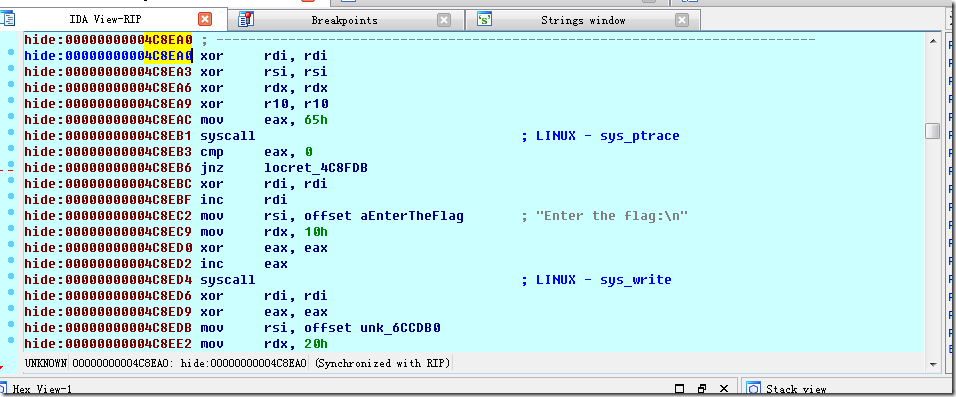
在4C8EA0也有类似的输出，怀疑正式运行时是这里。恢复函数失败，只能动态调试

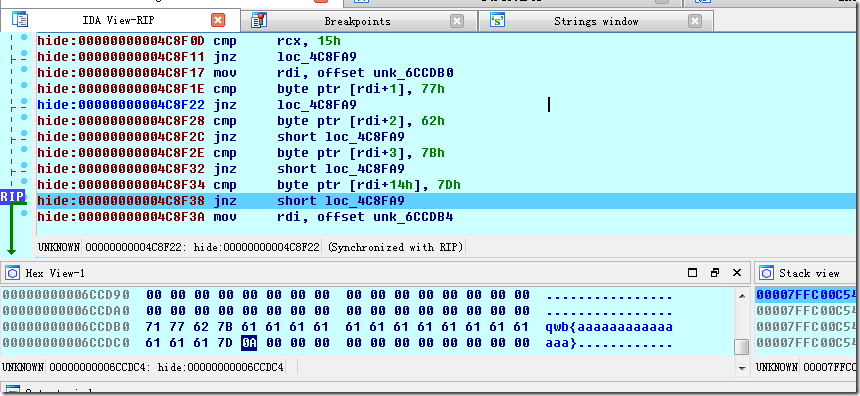
上面这里判断是不是qwb{}格式，构造payload

然后调用3次以下2个函数，输入内容为qwb{0123456789abcdef}中间部分的0123456789abcdef

sub_4C8CC0(__int64 a1)

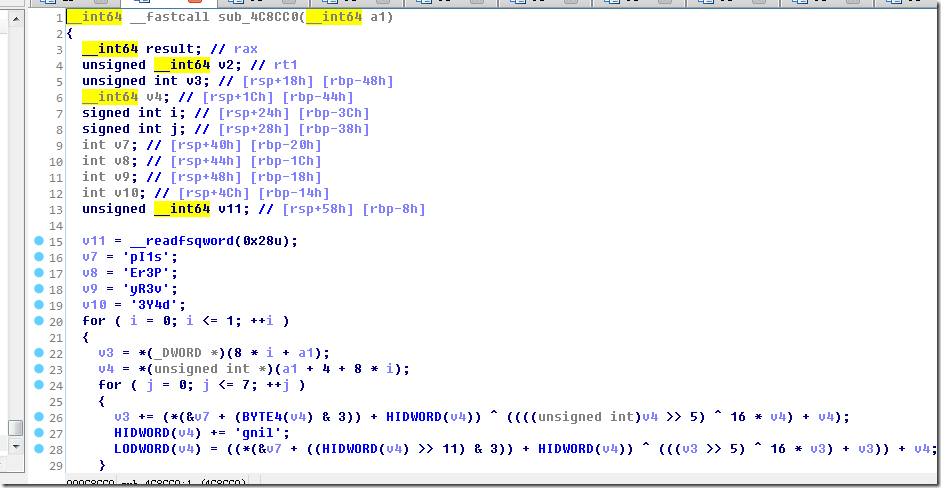
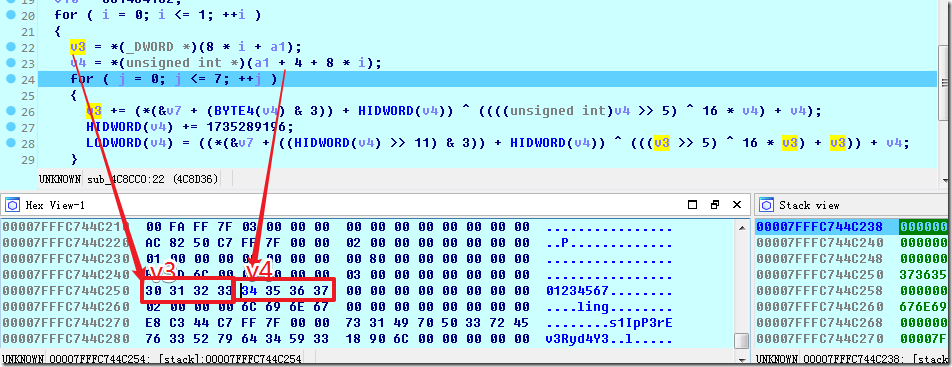
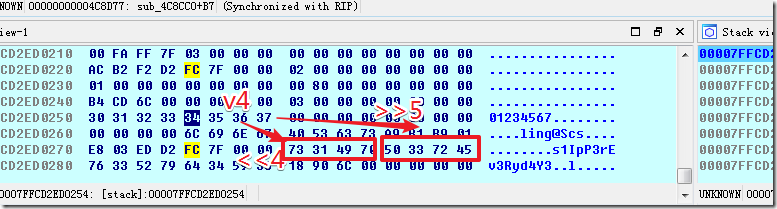
这部分算法恢复见test2.py中的loop_j

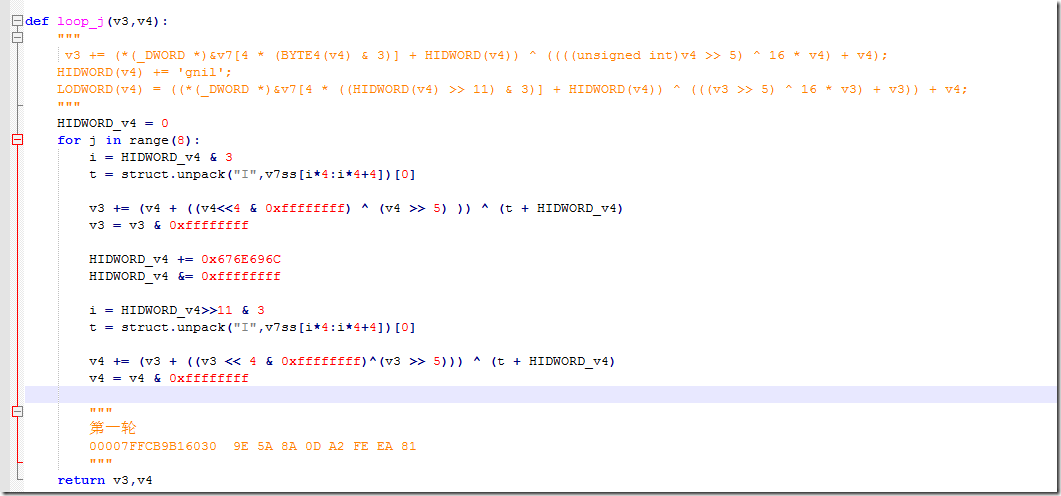
sub_4C8E50——按位异或

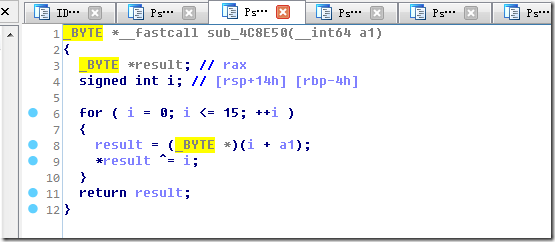
目标：rdi（qwb{}中间内容经过上面的多次变换后） == rsi（如下），

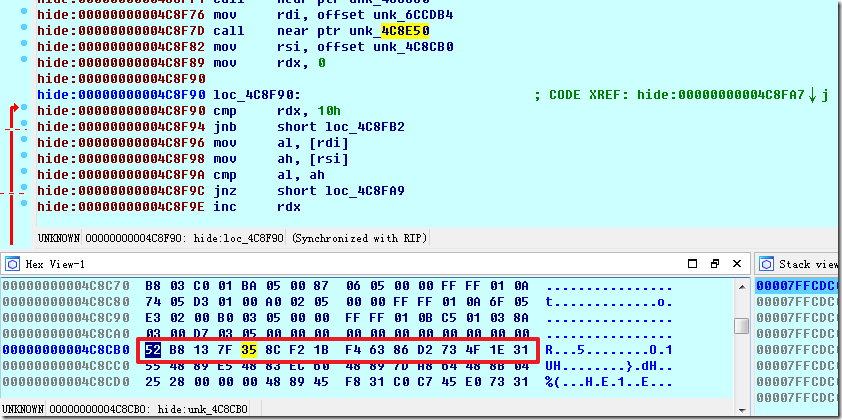
经过test2.py的逆向，得到一个有意义的输入串f1Nd_TH3HldeC0dE

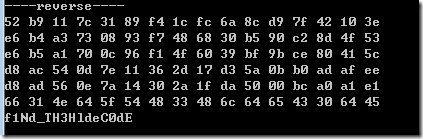
所以认为flag是qwb{f1Nd_TH3HldeC0dE}

实际运行，输入完qwb{f1Nd_TH3HldeC0dE}后，用ctrl+d可以看到成功（回车不行，因为用sys_read会连回车也认为是字符？）

但是实际为何会运行到hide脚本，就没有分析了，因为ptrace自己后发生什么事情，很难搞。

以下是通过IDA运行并跳过反调试的脚本

from idaapi import *

from idc import *

run_to(0x4009ef)

GetDebuggerEvent(WFNE_SUSP, -1)

SetRegValue(0x4C8EA0,"RIP")

GetDebuggerEvent(WFNE_SUSP, -1)

run_to(0x4C8EB3)

GetDebuggerEvent(WFNE_SUSP, -1)

SetRegValue(0,"RAX")

run_to(0x4C8CC0)

脚本含义