堆排序与优先队列——算法导论(7)

1. 预备知识

1.1 基本概念

先来介绍堆的概念。

如图（a），（二叉）堆是一个近似的完全二叉树。树中的每一个结点对应数组中的一个元素。除了最底层外，该树是完全充满的，而且从左向右填充。

堆可以用数组来实现，如图（b）所示。堆中的节点在数组中，按树广度优先遍历的结果依次排列。在这种实现方式下，堆应该包含两个基本属性：length，给出数组的长度；heap-size，表示堆中有多少个元素。

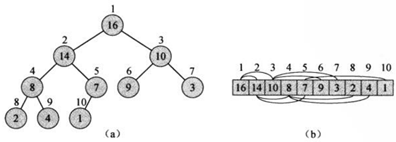
由于堆的这种特殊的结构，我们可以很容易根据一个结点的下标i计算出它的父节点、左孩子、右孩子的下标。计算公式如下：

parent(i) = i / 2;

left-child(i) = 2i;

right-child(i) = 2i + 1;

二叉堆有两种形式：最大堆、最小堆。在这两种形式中，结点的值都要满足以上给出的堆的性质。二者的差异在于：在最大堆中，父节点的值均大于子节点（根节点因为没有父节点，所以不要求在内）；最小堆相反。

在用途上，最大堆通常用在堆排序算法中；最小堆通常用于构建优先队列。

我们定义，堆中每个结点的高度为该结点到叶结点最长简单路径上，边的数目。而堆的高度，就为根结点的高度。

1.2. 维护堆的性质

我们用 MAX-HEAPIFY 函数来维护以下标 i 为根结点的子树的最大堆性质（这里假定以下标left(i)为根结点的子树和以下标为right(i)为根结点的子树满足最大堆的性质）。MAX-HEAPIFY函数的输入为一个数组A和一个下标 i ，其思想是通过让 A[i] 的值在最大堆中“逐级下降”，从而使得以下标 i 为结点的子树重新遵循最大堆的性质。

下面是该算法的伪代码：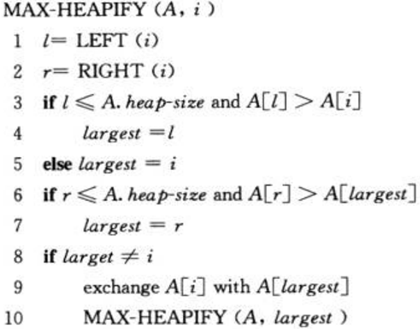

1.3 建堆

我们可以用置底向上的方法，利用过程 MAX-HEAPIFY 把一个大小为 n=A.length 的数组A[1~n]转化为最大堆。原理很简单，就是从倒数第2层（为说明方便，我们把根结点叫做第1层，其子结点叫做第2层，依次类推）开始，调用MAX-HEAPFY方法，直至到根结点。算法描述如下：

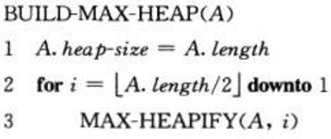
可以用以前介绍的循环不变式（见算法基础——算法导论(1)）去证明以上算法的正确性：

初始化：在第一次循环迭代之前，需要构建的堆只包含最底层元素，当然满足堆的性质（这被称为平凡最大堆）。

保持：假设循环迭代式在第i（1 ≤ i < A.length/2）次迭代时是成立的，即以下标为i的元素为根结点的子树满足最大堆的性质；当i = i + 1时，max-heapify方法的执行保证了，当以下标left(i)为根结点的子树和以下标为right(i)为根结点的子树满足最大堆的性质时，以下标i为根结点的子树满足最大堆的性质（这正是该方法的作用）。因此循环迭代式具有保持性。

终止：当循环终止时，根据保持性，需要构建的堆由初始化的只包含最底层元素，扩展为包含所有元素。

因此，算法正确。

2. 堆排序(heap-sort)

了解了以上的预备知识后，我们正式开始介绍堆排序。

下面给出堆排序算法：

简单地说，其原理是基于最大堆的根结点元素最大的性质。我们首先将待排序的数组构建为最大堆数组。然后遍历整棵树，每次遍历“取出”根结点，再调用 MAX-HEAPIFY 维护子树的最大堆性质，这样就能保证遍历时每次“取出”的元素是当前剩余元素中最大的。（“取出”不一定要真正的把元素从数组里取出，我们可以通过改变heap-size的值来达到此效果）

下面给出Java实现代码：

 // 测试
 public static void main(String[] args) {
     int[] array = { 2, 1, 6, 3, 9, 7, 4, 0, 4 };
     heapSort(array);
     printArray(array);
 }

 /**
  * 堆排序
  * @param array
  */
 public static void heapSort(int[] array) {
     buildMaxHeap(array);
     int heapSize = array.length;
     for (int i = array.length - 1; i > 0; i--) {
         int temp = array[i];
         array[i] = array[0];
         array[0] = temp;
         heapSize--;
         maxHeapify(array, 0, heapSize);
     }
 }

 /**
  * 维护以index为根节点的树的最大堆性质
  *
  * @param array
  *            堆数组
  * @param index
  *            要维护的结点
  */
 public static void maxHeapify(int[] array, int index, int heapSize) {
     int leftIndex = 2 * index + 1;
     int rightIndex = 2 * index + 2;
     int largeIndex;
     if (leftIndex < heapSize && array[leftIndex] > array[index]) {
         largeIndex = leftIndex;
     } else {
         largeIndex = index;
     }
     if (rightIndex < heapSize && array[rightIndex] > array[largeIndex]) {
         largeIndex = rightIndex;
     }
     if (largeIndex != index) {
         int temp = array[largeIndex];
         array[largeIndex] = array[index];
         array[index] = temp;
         maxHeapify(array, largeIndex, heapSize);
     }
 }

 /**
  * 将array构建为最大堆数组
  *
  * @param array
  */
 public static void buildMaxHeap(int[] array) {
     int heapSize = array.length;
     for (int i = (array.length - 2) / 2; i > -1; i--) {
         maxHeapify(array, i, heapSize);
     }
 }

 public static void printArray(int[] array) {
     for (int i : array) {
         System.out.print(i + "");
     }
     System.out.println();
 }

结果：

3. 算法分析

我们按照main方法的执行顺序来逐步分析算法的时间代价。

① 先分析buildMaxHeap方法。要分析buildMaxHeap方法先要分析maxHeapify方法。

我们假设maxHeapify方法在每次执行时，都会进行执行递归操作，在最坏的情况（树的最底层恰好半满）下，子树的规模是原来的2/3。其他时间为常量θ(1);因此我们可以得到运行时间的递归式：

T(n) ≤T(2n/3)+θ(1)，

可解得，T(n) = O(lgn)，即maxHeapify方法的时间复杂度为O(lgn)。

我们对buildMaxHeap方法进行粗略估计，它会调用O(n)次maxHeapify方法，而其他时间为常量θ(1)，因此buildMaxHeap方法总的时间复杂度为：O(nlgn)。

但是这个上界显然不是渐进紧确的。因为事实上maxHeapify方法时间与结点的高度有关，而且大部分结点的高度都很小。

我们可以利用如下性质得到一个紧确的上界：包含n个元素的堆的高度是[lgn]（[]表示向下取整）；高度为h的堆至多包含【n/2^(h+1)】（【】表示向上去整）。

我们设在高度为h的结点上运行maxHeapify方法的时间代价是O(h)，那么buildMaxHeap方法的总时间代价可以表示为：

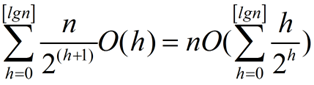
而

所以，buildMaxHeap的时间复杂度为O(n)。

②我们再分析heapSort中的for循环。for循环执行n-1次，而每次循环执行的时间复杂度为O(lgn)，因此总的时间复杂度为O(nlgn)。

③ 其他运行时间为常量O(1)。

因此heapSort的时间复杂度为O(nlgn)。

4. 优先队列(priority queue)

这一小节我们关注：如何基于最大堆来实现最大优先队列(priority queue)。

4.1 什么是最大优先队列(priority queue)

最大优先队列(priority queue)是一种用来维护一组数据构成的集合S的数据结构。其中的每一个元素都有一个关键值(key)。一个最大优先队列支持以下操作：

① maximum(s)：返回集合s中具有最大关键字(key)的元素；

② extractMax(s)：去掉并返回集合s中具有最大关键字(key)的元素；

③ increaseKey(s, x, k)：将元素x的值增加到k（假设k的值不小于x）；

④ insert(s, x)：把元素x插入集合s中，即s = s U x。

4.2 方法的实现

① maximum(s)的实现很简单，直接返回根结点：

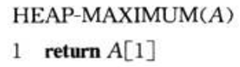
② extractMax(s)的实现同样简单，在返回根结点之前，先将其从树中“摘掉”，将堆数组中的最后一个元素挂载到根结点，再执行maxHeapify方法维护最大堆性质：

③ increaseKey(s, x, k)的实现方式是将下标为x的结点的值修改为k后，不断的与其父结点的值相比较，直至最终找到合适的位置，使得满足最大堆性质：

④ insert(s, x)方法利用了increaseKey(s, x, k)方法。具体做法是，先将x赋一个非常小的值，然后调用increaseKey(s, x, k)方法修改x的值为k。

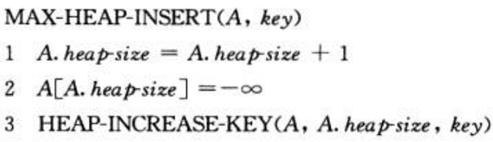
4.3 补充说明

以上方法的具体代码实现和时间代价分析就不给出了，与堆排序类似（实际上就是堆排序的应用推演）。

最大优先队列的应用应该是很广泛的。比如用于任务调度，我们可以用insert(s, x)方法来提交一个任务；用extractMax(s)方法来获取任务；而increaseKey(s, x, k)方法可以用来修改任务的优先级。

显然，最大优先队列里记录的只是需要存储的对象的句柄(handle)，其具体表现形式依赖于具体的应用程序。

与最大优先队列相反的是最小优先队列，它的实现方式基本与最大优先队列一致（是相反的），它有着不同的应用场景，以后会给出。