bzoj 3489 A simple rmq problem - 线段树

Description

因为是OJ上的题，就简单点好了。给出一个长度为n的序列，给出M个询问：在[l,r]之间找到一个在这个区间里只出现过一次的数，并且要求找的这个数尽可能大。如果找不到这样的数，则直接输出0。我会采取一些措施强制在线。

Input

第一行为两个整数N,M。M是询问数，N是序列的长度（N<=100000，M<=200000)

第二行为N个整数，描述这个序列{ai}，其中所有1<=ai<=N

再下面M行，每行两个整数x，y，

询问区间[l,r]由下列规则产生（OIER都知道是怎样的吧>_<)：

l=min(（x+lastans)mod n+1,(y+lastans）mod n+1);

r=max(（x+lastans)mod n+1,(y+lastans）mod n+1);

Lastans表示上一个询问的答案，一开始lastans为0

Output

一共M行，每行给出每个询问的答案。

Sample Input

10 10
6 4 9 10 9 10 9 4 10 4
3 8
10 1
3 4
9 4
8 1
7 8
2 9
1 1
7 3
9 9

Sample Output

4
10
10
0
0
10
0
4
0
4

HINT

注意出题人为了方便，input的第二行最后多了个空格。

2015.6.24新加数据一组，2016.7.9放至40S,600M,但未重测

Source

by zhzqkkk

---

　　题目大意 询问区间内只出现1次数的最大值。强制在线。

　　考虑每位置上的数会对哪些询问作出贡献。

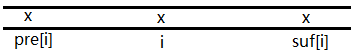
　　显然要让位置i对答案产生贡献询问的区间需要满足 pre[i] < l <= i 并且 i <= r < suf[i] 。

　　那么就可以将每个询问(l, r)看成二维平面内的一个点。

　　这样的话，每个位置对答案的贡献就可以通过2维线段树来进行维护。

　　为了防止MLE，所以采取标记永久化的方案。但是注意修改操作是和线段树维护的信息取max。

Code

 /**
  * bzoj
  * Problem#3489
  * Accepted
  * Time: 21836ms
  * Memory: 227780k
  */
 #include <bits/stdc++.h>
 using namespace std;
 typedef bool boolean;

 typedef class SegTreeNode {
     public:
         SegTreeNode* val;
         SegTreeNode *l, *r;

         SegTreeNode(int val = ):val((SegTreeNode*)val) {        }
         SegTreeNode(int val, SegTreeNode* org):val((SegTreeNode*)val) {
             l = r = org;
         }

         int intvalue() {
             return (int)val;
         }

         SegTreeNode*& pnodeval() {
             return val;
         }

         void set(int x) {
             val = (SegTreeNode*)x;
         }
 }SegTreeNode;

 #define PLimit 10000000

 //int alloced = 0;
 SegTreeNode pool[PLimit];
 SegTreeNode null = SegTreeNode(, &null);
 SegTreeNode* top = pool;

 SegTreeNode* newnode() {
 //    alloced++;
     if(top >= pool + PLimit)
         return new SegTreeNode(, &null);
     *top = SegTreeNode(, &null);
     return top++;
 }

 typedef class SegTree {
     public:
         int n;
         SegTreeNode* rt;

         SegTree() {        }
         SegTree(int n):n(n), rt(newnode()) {        }

         void update2(SegTreeNode*& node, int l, int r, int ql, int qr, int val) {
             if(node == &null || node == NULL)
                 node = newnode();
             if(l == ql && r == qr) {
                 if(val > node->intvalue())
                     node->set(val);
                 return;
             }
             int mid = (l + r) >> ;
             if(ql <= mid)
                 update2(node->l, l, mid, ql, (qr > mid) ? (mid) : (qr), val);
             if(qr > mid)
                 update2(node->r, mid + , r, (ql > mid) ? (ql) : (mid + ), qr, val);
         }

         void update(SegTreeNode*& node, int l, int r, int ql, int qr, int qx, int qy, int val) {
             if(node == &null)
                 node = newnode();
             if(l == ql && r == qr) {
                 update2(node->pnodeval(), , n, qx, qy, val);
                 return;
             }
             int mid = (l + r) >> ;
             if(ql <= mid)
                 update(node->l, l, mid, ql, (qr > mid) ? (mid) : (qr), qx, qy, val);
             if(qr > mid)
                 update(node->r, mid + , r, (ql > mid) ? (ql) : (mid + ), qr, qx, qy, val);
         }

         int query2(SegTreeNode*& node, int l, int r, int idx) {
             if(node == NULL || node == &null)
                 return ;
             if(l == idx && r == idx)
                 return node->intvalue();
             int mid = (l + r) >> , rt = node->intvalue(), cmp = ;
             if(idx <= mid)
                 cmp = query2(node->l, l, mid, idx);
             else
                 cmp = query2(node->r, mid + , r, idx);
             return (cmp > rt) ? (cmp) : (rt);
         }

         int query(SegTreeNode*& node, int l, int r, int idx, int bidx) {
             if(node == &null)
                 return ;
             if(l == idx && r == idx)
                 return query2(node->pnodeval(), , n, bidx);
             int mid = (l + r) >> , rt = query2(node->pnodeval(), , n, bidx), cmp;
             if(idx <= mid)
                 cmp = query(node->l, l, mid, idx, bidx);
             else
                 cmp = query(node->r, mid + , r, idx, bidx);
             return (cmp > rt) ? (cmp) : (rt);
         }
 }SegTree;

 int n, m;
 int *ar;
 int *pre, *suf;
 int *head;
 SegTree st;

 inline void init() {
     scanf("%d%d", &n, &m);
     st = SegTree(n);
     ar = new int[(n + )];
     pre = new int[(n + )];
     suf = new int[(n + )];
     head = new int[(n + )];
     for(int i = ; i <= n; i++)
         scanf("%d", ar + i);
 }

 inline void solve() {
     memset(head, , sizeof(int) * (n + ));
     for(int i = ; i <= n; i++)
         pre[i] = head[ar[i]], head[ar[i]] = i;
     fill(head, head + n + , n + );
     for(int i = n; i; i--)
         suf[i] = head[ar[i]], head[ar[i]] = i;

     for(int i = ; i <= n; i++)
         st.update(st.rt, , n, pre[i] + , i, i, suf[i] - , ar[i]);//, fprintf(stderr, "%d: Memory Usage: %d (%d nodes)\n", i, alloced * sizeof(SegTreeNode), alloced);
     int lastans = , x, y;
     while(m--) {
         scanf("%d%d", &x, &y);
         x = (x + lastans) % n + ;
         y = (y + lastans) % n + ;
         if(x > y)    swap(x, y);
         lastans = st.query(st.rt, , n, x, y);
         printf("%d\n", lastans);
     }
 }

 int main() {
     init();
     solve();
     return ;
 }