codeforces 459E

codeforces 459E

E. Pashmak and Graph

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Pashmak's homework is a problem about graphs. Although he always tries to do his homework completely, he can't solve this problem. As you know, he's really weak at graph theory; so try to help him in solving the problem.

You are given a weighted directed graph with n vertices and m edges. You need to find a path (perhaps, non-simple) with maximum number of edges, such that the weights of the edges increase along the path. In other words, each edge of the path must have strictly greater weight than the previous edge in the path.

Help Pashmak, print the number of edges in the required path.

Input

The first line contains two integers n, m (2 ≤ n ≤ 3·105; 1 ≤ m ≤ min(n·(n - 1), 3·105)). Then, m lines follows. The i-th line contains three space separated integers: ui, vi, wi (1 ≤ ui, vi ≤ n; 1 ≤ wi ≤ 105) which indicates that there's a directed edge with weight wi from vertex ui to vertex vi.

It's guaranteed that the graph doesn't contain self-loops and multiple edges.

Output

Print a single integer — the answer to the problem.

Sample test(s)

input

3 3 
1 2 1 
2 3 1 
3 1 1

output

1

input

3 3 
1 2 1 
2 3 2 
3 1 3

output

3

input

6 7 
1 2 1 
3 2 5 
2 4 2 
2 5 2 
2 6 9 
5 4 3 
4 3 4

output

6

Note

In the first sample the maximum trail can be any of this trails:

.

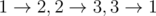
In the second sample the maximum trail is

.

In the third sample the maximum trail is

.

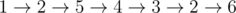
题目类型：DP

思路：1. dfs铁定超时，因为一开始没想到办法如何两条边去更新一个点时存储哪一个

2.看到排序之后立马有思路，但是还是超时？！为什么？因为我不是更新的点，是去更新的边，这样一条边可能会被访问很多很多次，而如果访问点的话，一条边只需要被访问一次（当然后来修改为AC的之后一条边可能被访问2次），当然就算不超时，后面也会wa的为什么呢？下面解释、、

3.修改为更新点，wa一次。。因为当更新第一次后，后面相同的wei可能会被放弃，最后面的一组样例就是这样错的，使用vector存储要更新的点

4.改了之后还是wa，因为要更新的点覆盖了之前这个点的更新信息，所以用pair存储就可以了

 #include<iostream>

 #include<cstdio>

 #include<cstring>

 #include<vector>

 #include<cmath>

 #include<map>

 #include<algorithm>

 #define M(a,b) memset(a,b,sizeof(a))

 using namespace std;

 int n,m;

 int res;

 int p[];

 int psave[];

 struct ed

 {

     int from;

     int to;

     int wei;

     bool operator < (const ed& rhs) const

     {

         return wei<rhs.wei;

     }

 }edge[];

 vector<pair<int,int> > g;

 void dp()

 {

     int pre = edge[].wei;

     //cout<<u<<'!'<<endl;

     for(int i = ;i<m;i++)

     {

         if(pre!=edge[i].wei)

         {

             pre = edge[i].wei;

             for(int j = ;j<g.size();j++)

                 if(g[j].second>p[g[j].first]) p[g[j].first] = g[j].second;

             g.clear();

         }

         //cout<<edge[i].from<<' '<<edge[i].to<<' '<<p[edge[i].from]<<' '<<pw[edge[i].from]<<endl;

         if(p[edge[i].from]+>p[edge[i].to])

         {

               g.push_back(make_pair(edge[i].to,p[edge[i].from]+));

               if(p[edge[i].from]+>res) res = p[edge[i].from]+;

         }

     }

     for(int j = ;j<g.size();j++)

             if(psave[g[j].second]>p[g[j].first]) p[g[j].first] = psave[g[j].second];

     return;

 }

 int main()

 {

    while(scanf("%d%d",&n,&m)==)

    {

        int u,v,w;

        res = ;

        M(p,);

        for(int i = ;i<m;i++)

        {

            scanf("%d%d%d",&u,&v,&w);

            edge[i].from = u;

            edge[i].to = v;

            edge[i].wei = w;

        }

        sort(edge,edge+m);

        //  cout<<temu<<endl;

        p[edge[].from] = ;

        dp();

        for(int i = ;i<n;i++)

        {

            if(p[i]>res)

             res = p[i];

        }

        printf("%d\n",res);

    }

    return ;

 }

 /*

 9 8

 1 2 1

 2 3 2

 4 5 1

 5 6 2

 6 3 3

 3 7 4

 7 8 5

 8 9 6

 */