二叉查找树之 Java的实现

参考：http://www.cnblogs.com/skywang12345/p/3576452.html

二叉查找树简介

二叉查找树(Binary Search Tree)，又被称为二叉搜索树。
它是特殊的二叉树：对于二叉树，假设x为二叉树中的任意一个结点，x节点包含关键字key，节点x的key值记为key[x]。如果y是x的左子树中的一个结点，则key[y] <= key[x]；如果y是x的右子树的一个结点，则key[y] >= key[x]。那么，这棵树就是二叉查找树。如下图所示：

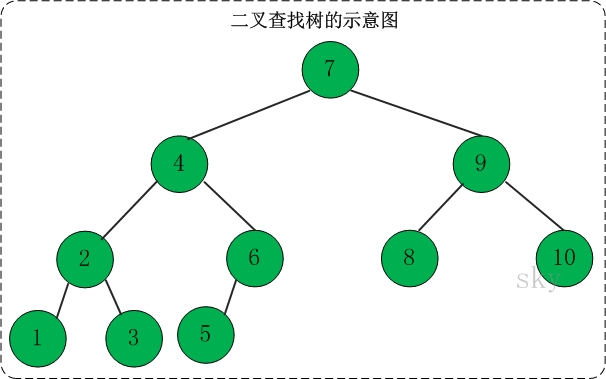
在二叉查找树中：
(01) 若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
(02) 任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
(03) 任意节点的左、右子树也分别为二叉查找树。
(04) 没有键值相等的节点（no duplicate nodes）。

二叉查找树的Java实现

1. 二叉查找树节点的定义

public class BSTree<T extends Comparable<T>> {

    private BSTNode<T> mRoot;    // 根结点

    public class BSTNode<T extends Comparable<T>> {
        T key;                // 关键字(键值)
        BSTNode<T> left;      // 左孩子
        BSTNode<T> right;     // 右孩子
        BSTNode<T> parent;    // 父结点

        public BSTNode(T key, BSTNode<T> parent, BSTNode<T> left, BSTNode<T> right) {
            this.key = key;
            this.parent = parent;
            this.left = left;
            this.right = right;
        }
    }

        ......
}
        

BSTree是二叉树，它保护了二叉树的根节点mRoot；mRoot是BSTNode类型，而BSTNode是二叉查找树的节点，它是BSTree的内部类。BSTNode包含二叉查找树的几个基本信息：
(01) key -- 它是关键字，是用来对二叉查找树的节点进行排序的。
(02) left -- 它指向当前节点的左孩子。
(03) right -- 它指向当前节点的右孩子。
(04) parent -- 它指向当前节点的父结点。

2 遍历

这里讲解前序遍历、中序遍历、后序遍历3种方式。

2.1 前序遍历
若二叉树非空，则执行以下操作：
(01) 访问根结点；
(02) 先序遍历左子树；
(03) 先序遍历右子树。

前序遍历代码

private void preOrder(BSTNode<T> tree) {
    if(tree != null) {
        System.out.print(tree.key+" ");
        preOrder(tree.left);
        preOrder(tree.right);
    }
}

public void preOrder() {
    preOrder(mRoot);
}

2.2 中序遍历

若二叉树非空，则执行以下操作：
(01) 中序遍历左子树；
(02) 访问根结点；
(03) 中序遍历右子树。

中序遍历代码

private void inOrder(BSTNode<T> tree) {
    if(tree != null) {
        inOrder(tree.left);
        System.out.print(tree.key+" ");
        inOrder(tree.right);
    }
}

public void inOrder() {
    inOrder(mRoot);
}

2.3 后序遍历

若二叉树非空，则执行以下操作：
(01) 后序遍历左子树；
(02) 后序遍历右子树；
(03) 访问根结点。

后序遍历代码

private void postOrder(BSTNode<T> tree) {
    if(tree != null)
    {
        postOrder(tree.left);
        postOrder(tree.right);
        System.out.print(tree.key+" ");
    }
}

public void postOrder() {
    postOrder(mRoot);
}

看看下面这颗树的各种遍历方式：

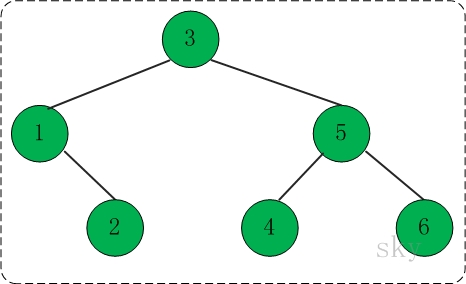
对于上面的二叉树而言，
(01) 前序遍历结果： 3 1 2 5 4 6
(02) 中序遍历结果： 1 2 3 4 5 6 
(03) 后序遍历结果： 2 1 4 6 5 3

3. 查找

递归版本的代码

/*
 * (递归实现)查找"二叉树x"中键值为key的节点
 */
private BSTNode<T> search(BSTNode<T> x, T key) {
    if (x==null)
        return x;

    int cmp = key.compareTo(x.key);
    if (cmp < 0)
        return search(x.left, key);
    else if (cmp > 0)
        return search(x.right, key);
    else
        return x;
}

public BSTNode<T> search(T key) {
    return search(mRoot, key);
}

非递归版本的代码

/*
 * (非递归实现)查找"二叉树x"中键值为key的节点
 */
private BSTNode<T> iterativeSearch(BSTNode<T> x, T key) {
    while (x!=null) {
        int cmp = key.compareTo(x.key);

        if (cmp < 0)
            x = x.left;
        else if (cmp > 0)
            x = x.right;
        else
            return x;
    }

    return x;
}

public BSTNode<T> iterativeSearch(T key) {
    return iterativeSearch(mRoot, key);
}

4. 最大值和最小值

查找最大值的代码

/*
 * 查找最大结点：返回tree为根结点的二叉树的最大结点。
 */
private BSTNode<T> maximum(BSTNode<T> tree) {
    if (tree == null)
        return null;

    while(tree.right != null)
        tree = tree.right;
    return tree;
}

public T maximum() {
    BSTNode<T> p = maximum(mRoot);
    if (p != null)
        return p.key;

    return null;
}

查找最小值的代码

/*
 * 查找最小结点：返回tree为根结点的二叉树的最小结点。
 */
private BSTNode<T> minimum(BSTNode<T> tree) {
    if (tree == null)
        return null;

    while(tree.left != null)
        tree = tree.left;
    return tree;
}

public T minimum() {
    BSTNode<T> p = minimum(mRoot);
    if (p != null)
        return p.key;

    return null;
}

 

6. 插入

插入节点的代码：

public  BinaryNode<T> insert(T x,BinaryNode<T> t)
{
　　if(t==null)
　　　　return new BinaryNode<>(x,null,null);
　　
　　int r=x.compareTo(t.element);
　　if(r<0)
　　　　t.left=insert(x,t.left);
　　else if(r>0)
　　　　t.right=insert(x,t.right);
　　else
　　　　;//重复，不做

　　return t;
}

7. 删除

删除节点的代码

如果节点是一片树叶，则直接被删除；如果节点有一个儿子，用儿子代替此节点；如果有两个儿子，用其右子树的最小数据代替该节点的数据，并删除右子树的该节点（最小节点）,此时不能直接用右子树的最小节点代替此节点，因为最小节点可能有孩子，直接代替，就会混乱。

public BinaryNode<T> remove(T x,BinaryNode<T> t){
　　if(t==null)
　　　　return t;
　　
int r=x.compareTo(t.element);

if(r<0)
　　t.left=remove(x,t.left);
else if(r>0)
　　t.right=remove(x,t.right);
//找到节点以后
else if(t.left!=null&&t.right!=null)//两个儿子
{
　　t.element=findMin(t.right).element;
　　t.right=remove(t.element,t.right);
}
else //一个儿子。这种情况同时也包含了没有孩子的情况。左节点不为空就用左节点代替，如果左节点为空，则用右节点代替，右节点也可能为空。
　　t=(t.left!=null)?t.left:t.right;

return t;

}