Cookie&Session（会话技术）

一．Cookie技术

从打开一个游览器访问某个站点，到关闭这个游览器的整个过程成为一次会话

会话技术分为Cookie和Session

Cookie：数据存储在客服端本地，减少对服务端的存储的压力，安全性相对较低，客服端也清楚Cookie

Session：将数据存储到服务器端，安全性相对好，增加服务器压力

一、Cookie发送技术实现的四步走
1.创建Cookie实例化对象
Cookie cookie = new Cookie(String cookieName,String cookieValue);
例子：
Cookie cookie = new Cookie("userName","123456");
2.设置Cookie在客服端的持久化时间（可省略）
cookie.setMaxAge(int seconds)//秒
例子：10分钟
cookie.setMaxAge(10*60);
3.设置携带Cookie的路径（可省略）
cookie.setPath(String Path);
例子：全局的Cookie的配置
cookie.setPath("/")
4.发送cookie到客服端
response.addCookie(Cookie cookie);

第一步：
创建cookie注意事项

cookie中不能使用中文显示

第二步：

如果不设置持久化时间则以会话级，即当窗口关闭时就清除Cookie，如果设置持久化则将Cookie中的信息固化到磁盘上，到时间时游览器自动清理Cookie文件

第三步：

如果不设置携带路径，那么该cookie信息会在访问产生该cookie的 ，web资源所在的路径都携带cookie信息

删除Cookie：

只要使用同名同路径的持久化时为0的Cookie进行覆盖

二、服务器端接受客户端携带的Cookie、
Cookie[] cookies = request.getCookies()
for(Cookie cookie : Cookies){
　　if(cookie.getName().equal(cookieName)){
　　　　String cookieValue = cookie.getValue();
　　}
}

二、Session技术

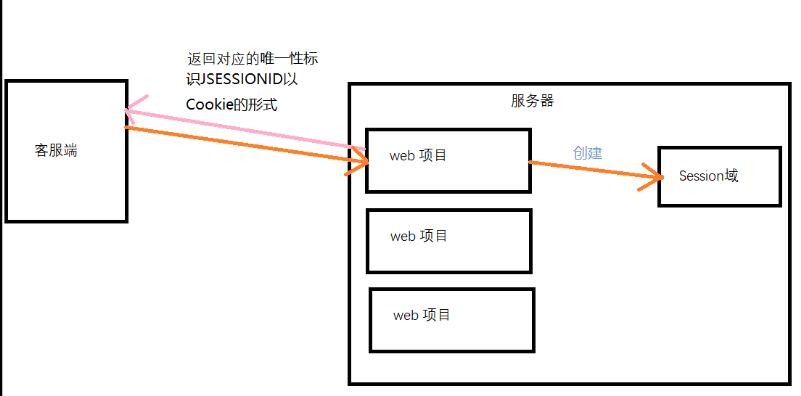
Session技术是将数据存储在服务器端的技术，会为每个客户端都创建一块内存空间 存储客户的数据，但客户端需要每次都携带一个标识ID去服务器中寻找属于自己的内存空间。所以说Session的实现是基于Cookie，Session需要借助于Cookie存储客 户的唯一性标识JSESSIONID

1. 

1．获得Session对象
HttpSession session = request.getSession();
此方法会获得专属于当前会话的Session对象，如果服务器端没有该会话的Session对象会创建一个新的Session返回，如果已经有了属于该会话的Session直接将已有的Session返回
（实质就是根据JSESSIONID判断该客户端是否在服务器上已经存在session了）
2.向Session对象中存取数据
session.setAttribute(String name,object obj);
session.getAttribute(String name);
session.removeAttribute(String name);

Session对象的生命周期

1. 服务器（非正常关闭）
2. session过期/失效，时间是从不开始访问服务器资源开始
3. 手动销毁session ——session.invalidate();

　　 默认：在一次会话中，也就是说在，一次会话中任何资源公用一个session对象