二叉树的基本操作（含Huffman树）

大二时候写的烂代码，翻出来复习复习（o(╯□╰)o）。

代码：

#include <stdio.h>
#include <stdlib.h>
#define  Max_Size 100
struct Binode{
  char res;
  struct Binode *lchild,*rchild;
};
struct Binode* First_Creat_Bitree(){//建立一棵二叉树，这里按照先序建立二叉树是有条件的，输入的序列中包含空节点。
  char ch;
  struct Binode *p;
  scanf("%c",&ch);
  if(ch==' ')
  p=NULL;
  else{
  p=(struct Binode *)malloc(sizeof(struct Binode));
  p->res=ch;
  p->lchild=First_Creat_Bitree();
  p->rchild=First_Creat_Bitree();
  }
  return p;
}

void PreOrder_Travel_Bitree(struct Binode *p){//按先序遍历二叉树
   if(p){
    printf("%c ",p->res);
    PreOrder_Travel_Bitree(p->lchild);
    PreOrder_Travel_Bitree(p->rchild);
   }
}

int max(int a,int b){
  return (a>b)?a:b;
}
int Get_High(struct Binode *p){//求一棵二叉树的高度
   if(p==NULL)
    return ;
   else
    return max(Get_High(p->lchild),Get_High(p->rchild))+;
}

int Get_Leaf_Node(struct Binode *p){//求二叉树的叶子节点个数
   if(p==NULL)
    return ;
   else if(p->lchild==NULL&&p->rchild==NULL)
    return ;
   else
    return Get_Leaf_Node(p->lchild)+Get_Leaf_Node(p->rchild);
}

struct Qnode{  //队列的基本操作
   struct Binode *data;       //入队的指针
   struct Qnode *next;
};
struct Link_Queue{
   struct Qnode *front;
   struct Qnode *rear;
};

void Init_Link_Queue(struct Link_Queue &s){
   s.front=s.rear=(struct Qnode*)malloc(sizeof(struct Qnode));
   if(s.front==NULL)
    printf("开辟内存失败\n");
   s.front->next=NULL;
}

void Enter_Link_Queue(struct Link_Queue &s,struct Binode *ch){
   struct Qnode *p;
   p=(struct Qnode*)malloc(sizeof(struct Qnode));
   p->data=ch;
   p->next=NULL;
   s.rear->next=p;
   s.rear=p;
}

void Delete_Link_Queue(struct Link_Queue &s){
   struct Qnode *p;
   if(s.front==s.rear)
   printf("队列已空\n");
   p=s.front->next;
   s.front->next=p->next;
   if(p==s.rear)
    s.rear=s.front;
   free(p);
}

int Empty_Link_Queue(struct Link_Queue &s){
    if(s.front==s.rear)
      return ;
    else
      return ;
}
void Level_Order_Travel(struct Binode *p){//层序遍历一棵二叉树
    struct Link_Queue s;
    struct Binode *tmp1,*tmp2;
    Init_Link_Queue(s);
    Enter_Link_Queue(s,p);
    while(!Empty_Link_Queue(s)){
     printf("%c ",s.front->next->data->res);
     tmp1=s.front->next->data->lchild;//出队列前将其左右儿子保存
     tmp2=s.front->next->data->rchild;
     Delete_Link_Queue(s);
     if(tmp1)
     Enter_Link_Queue(s,tmp1);//判断左右儿子是否为空，非空则入队列
     if(tmp2)
     Enter_Link_Queue(s,tmp2);
    }
}

struct Sq_Stack{      //栈的基本操作
  struct Binode **base;//入栈的是指针，因此栈顶指针与基址指针为二级指针
  struct Binode **top;
  int stack_size;
};

void Init_Sq_stack(struct Sq_Stack &s){
   s.base=(struct Binode** )malloc(Max_Size*sizeof(struct Binode * ));
   if(!s.base)
    printf("内存开辟失败\n");
   s.top=s.base;
   s.stack_size=Max_Size;
}

void Push_Sq_Stack(struct Sq_Stack &s,struct Binode *p){
    *(s.top)=p;
     s.top++;
}

void Pop_Sq_Stack(struct Sq_Stack &s){
    if(s.base==s.top)
    printf("栈已空\n");
    else
    s.top--;
}

int Empty_Sq_Stack(struct Sq_Stack &s){
    if(s.base==s.top)
      return ;
    else
      return ;
}

struct Binode* Get_Top(struct Sq_Stack &s){
    struct Binode *p;
    p=*(s.top-);
    return p;
}
void InOrder_Travel(struct Binode *p){//中序遍历二叉树的非递归算法
    struct Sq_Stack s;
    struct Binode *tmp,*tmp1;
    Init_Sq_stack(s);
    Push_Sq_Stack(s,p);
    while(!Empty_Sq_Stack(s)){
     while(Get_Top(s)){
      tmp=Get_Top(s);
      Push_Sq_Stack(s,tmp->lchild);
     }
     Pop_Sq_Stack(s);
     if(!Empty_Sq_Stack(s)){
      printf("%c ",Get_Top(s)->res);
      tmp1=Get_Top(s);//出栈前将其右儿子保存
      Pop_Sq_Stack(s);
      Push_Sq_Stack(s,tmp1->rchild);//右儿子入栈
     }
    }
}

int main()
{
    struct Binode *p;
    int high;
    int num;
    printf("建立一颗二叉树并用先序遍历将其输出\n");
    p=First_Creat_Bitree();
    PreOrder_Travel_Bitree(p);
    printf("\n");

    printf("求二叉树的高度\n");
    high=Get_High(p);
    printf("%d \n",high);

    printf("求该二叉树的叶子节点个数\n");
    num=Get_Leaf_Node(p);
    printf("%d \n",num);

    printf("二叉树的层序遍历\n");
    Level_Order_Travel(p);
    printf("\n");

    printf("二叉树的中序遍历：非递归\n");
    InOrder_Travel(p);
    printf("\n");
    return ;
}

测试结果：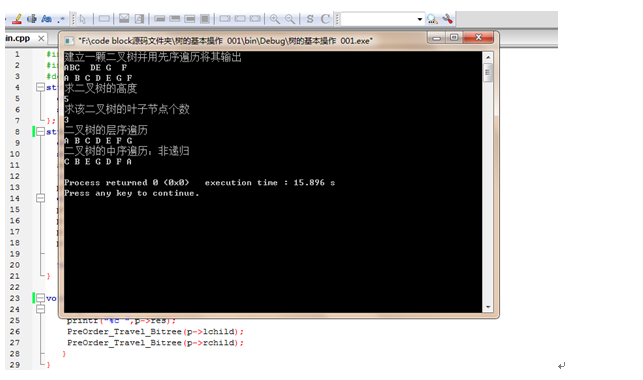

代码：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define  inf 99999999
struct HuffmanNode{
  int weight;
  int lchild,rchild,parent;
};
void Select(struct HuffmanNode *p,int n,int& num1,int& num2){
   int i;
   int min1,min2;
   min1=inf;
   for(i=;i<=n;i++){      //在还没有被选择的节点中，选择最小的节点
    if(p[i].parent==&&p[i].weight<min1){
      min1=p[i].weight;
    }
   }
   for(i=;i<=n;i++){
    if(p[i].parent==&&p[i].weight==min1){//找到该节点的序号
     num1=i;
     p[i].parent=;//将其父母置为非空，表明这个节点已经被选
     break;
    }
   }
   min2=inf;
    for(i=;i<=n;i++){      //在还没有被选择的节点中，选择次小的节点
     if(p[i].parent==&&p[i].weight<min2){
      min2=p[i].weight;
   }
}
     for(i=;i<=n;i++){
    if(p[i].parent==&&p[i].weight==min2){  //找到该节点的序号
     num2=i;
      p[i].parent=;//将其父母置为非空，表明这个节点已经被选
     break;
    }
   }
}
void Huffman_Coding(int n,struct HuffmanNode* &head,char** &HC){
  int m,i,s1,s2;//构造赫夫曼树
  if(n<)
  printf("无法构造赫夫曼树\n");
  m=*n-;
  head=(struct HuffmanNode *)malloc((m+)*sizeof(struct HuffmanNode));//0号元素不用
  for(i=;i<=m;i++){
   if(i<=n)
   scanf("%d",&head[i].weight);
   else
   head[i].weight=;
   head[i].lchild=;
   head[i].rchild=;
   head[i].parent=;
  }
  for(i=n+;i<=m;i++){
   Select(head,i-,s1,s2);
   head[s1].parent=i;
   head[s2].parent=i;
   head[i].lchild=s1;
   head[i].rchild=s2;
   head[i].weight=head[s1].weight+head[s2].weight;
  }
  char *cd;
  int start,c,f;   //对赫夫曼树进行编码
  HC=(char **)malloc((n+)*sizeof(char *));
  cd=(char *)malloc(n*sizeof(char));
  cd[n-]='\0';
  for(i=;i<=n;i++){
   start=n-;
   for(c=i,f=head[i].parent;f!=;c=f,f=head[f].parent){
     if(head[f].lchild==c)
     cd[--start]='';
     else
     cd[--start]='';
   }
   HC[i]=(char *)malloc((n-start)*sizeof(char));
   strcpy(HC[i],&cd[start]);
  }
  free(cd);
}
int main()
{
    int n,i;
    struct HuffmanNode *head;
    char **HC;
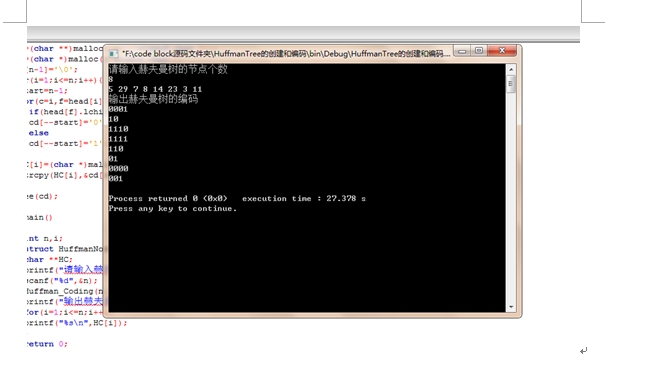
    printf("请输入赫夫曼树的节点个数\n");
    scanf("%d",&n);
    Huffman_Coding(n,head,HC);
    printf("输出赫夫曼树的编码\n");
    for(i=;i<=n;i++){
    printf("%s\n",HC[i]);
    }
    return ;
}

测试结果：