SVM3 Soft Margin SVM

之前分为两部分讨论过SVM。第一部分讨论了线性SVM，并且针对线性不可分的数据，把原始的问题转化为对偶的SVM求解。http://www.cnblogs.com/futurehau/p/6143178.html

然后考虑到特征数量特别特别多的时候，引入核函数的求解。http://www.cnblogs.com/futurehau/p/6149558.html

但是，之前也遗留了一个问题，就是比如高斯核函数或其他的核函数，虽然large margin能够在一定程度上防止过拟合，但是加入你的核函数太过于powerful的话，还是很有可能带来overfit的问题。另一方面，之前都是基于hard Margin,就是要求你所有的数据都给我分正确，这很容易带来过拟合的问题。

所以，接下来就讨论soft margin来避免过拟合问题。简单来说soft margin就是允许模型犯一些的错误。

一、soft margin 的引入

　　如下图所示，我们把原来的hard margin转化为soft margin,允许你在一些点处犯错误，但是最小化的式子就需要改变，意思是你错误的点要尽可能的少。c是用来权衡soft margin和容许犯的错误大小的超参数。

　　

　　稍微转化一下，表达式变为：

　　

　　但是我们发现，这样一个表达式并不是一个QP问题的，因为取0取1这个的引入导致是非线性的，那么我们应该怎么转化呢？

　　这样思考，之前我们只考虑了分正确没，对于不正确的都一视同仁。我们可不可以改变一下呢？对于那些不正确的，如果离边界比较远的其实是大错误，如果离边界比较近的其实是小错误，这两类错误其实是应该区分开来的，所以引入新的表达式如下：

　　

　　使用伊布c龙来记录违反的大小。表明你离我想要的值到底有多远。

　　这样，我们的问题就转化为：

　　

　　观察这个表达式，其实也可以看为给定松弛因子做目标函数，给定一个L2的正则项。

　　

二、soft margin 的 dual problem

　　好了，我们之前得到原始的soft margin 问题：

　　

　　类似于之前的方法，我们需要把这个问题转换为对偶问题。

　　写出拉格朗日函数：

　　

　　目标：

　　

　　对伊布c隆求导得到：

　　

　　带回原来表达式化简得到：

　　

　　得到最终的表达式：

　　

　　我们发现，最终的soft Margin dual problem的表达式和hard margin的表达式是内部是一样的，区别在于alpha的范围变化了。所以类似于之前的内部求偏导，我们可以得到：

　　

　　对比之前，唯一的区别就是alpha的范围改变了。

三、参数b的计算与图形分析

　　3.1 b的求解

　　之前得到了几个参数,还差b。b的表达和之前有所不同，这里特别分析。

　　

　　只有第二个等式C不等于alpha的时候才有确定的解，否则只能由kkt条件给出一个范围。

　　

　　3.2 C的影响

　　

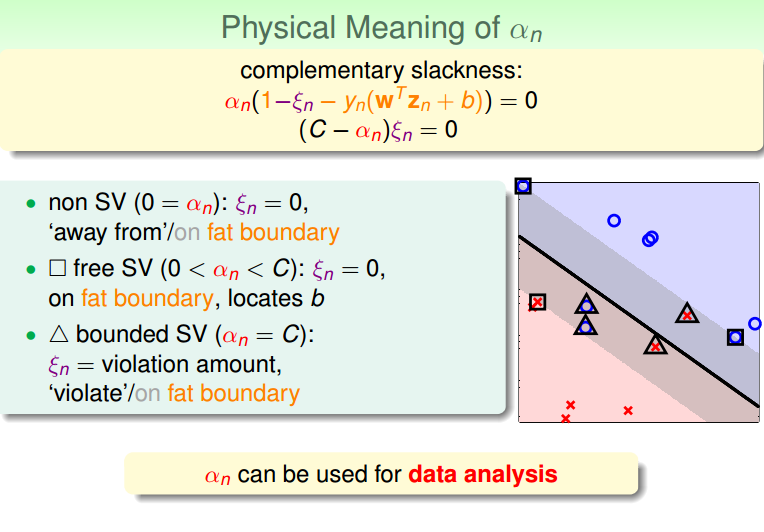
　　3.3 alpha的物理意义

　　

　　 

4. leave one out cross validation

　　还不太理解。