GPS围栏两个多边形相交问题的奇葩解法

前言

GPS测量仪测量的产地面积，然后提交到系统中，系统需要校验这块产地和其他产地是否有重叠，重叠超过10%就要提出警告这块产地已经被XXX登记入库了。GPS测量仪测量出来的数据是连续的经纬度坐标数据。现在的问题就转换成求一个一系列点围成的区域和其他区域是否存在交集。拿到这个需求我想应该很简单，网上应该有现成的代码吧。

先上成品

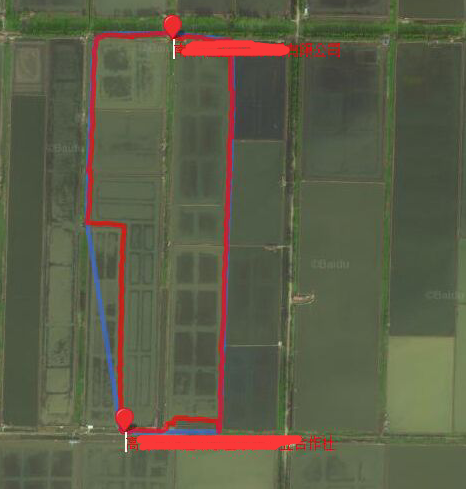
最初的想法

一开始想（XMin，YMin）应该是多边形的左下角，（XMax，YMin）应该是右下角，对应的找到4个顶点转换成矩形应该会好做一点吧。但是GPS测量出来的数据可不是都是垂直坐标轴的矩形，有的是斜着的，这样就找不到XMin和YMin了，而且如果是不规则的多边形怎么办，硬要转成矩形的话那样误差很大啊。

正统的解法

根据网上搜索到的资料显示，这个问题属于计算几何这门学科解决的问题。然后涉及了很多向量啊，向量的叉积啊，还有各种几何知识，如何在2-3天之内补习这些知识然后写出代码来，看起来是个很艰苦的过程。

1. 求点集的凹包，目的是减少多边形的点，一个GPS测量数据包含了少则500，多则3000多个连续的点集，所以要通过凹包来减少点集。
2. 求两个凹包多边形的交集Mix
3. 求交集Mix多边形的面积
4. 比较Mix多边形的面积和原始凹包多边形面积的比值

以上步骤最复杂的应该是求凹包和求交集了，原谅我学到凸包多边形就已经放弃了。

奇葩的解法

为何叫奇葩的解法， 其实是为了赚一波眼球而已，我最后选择的解法是通过gdi32.dll提供的windowsAPI来完成的，下面介绍下用到的几个API函数

根据点集创建一个多边形

IntPtr CreatePolygonRgn(Point[] lpPoint, int nCount, int nPolyFillMode);

　　

合并两个多边形，可以是OR/AND/XOR，这里用到的是AND

int CombineRgn(IntPtr dest, IntPtr src1, IntPtr src2, int flags);

　　

获取一个多边形的详细数据，拆解为若干个矩形

int GetRegionData(HandleRef hRgn, int size, IntPtr lpRgnData);

　　

所以最后我们的步骤就是

1. 根据GPS点集创建一个多边形
2. 再创建第二个多边形
3. 通过CombineRgn函数合并两个多边形，返回成功就表示有交集，返回失败就是无交集
4. 有交集的情况下，再通过GetRegionData获取交集和第一个多边形的信息
5. 计算GetRegionData里拆解出来的若干矩形的面积，长*宽
6. 比较交集的面积和第一个多边形面积的比值

整个过程看起来很简单，这里我上一些代码，把其中比较难的部分解释一下。

创建一个多边形

先引用dll

		[DllImport("gdi32")]
		private static extern IntPtr CreatePolygonRgn(Point[] lpPoint, int nCount, int nPolyFillMode);

　　

代码中Point是System.Drawing空间下的

X和Y*1000000是因为GPS信息是118.12334232这样的数据，如果直接取int的话就都变成118了，精度不够。

代码中IntPtr是句柄，windowsAPI编程中都是提供句柄，类似内存指针的玩意。

Point[] poin = new Point[gpsList.Count()];

for (int i = ; i < gpsList.Count(); i++)
{
    string[] xy = gpsList[i].Split(',');
    double x = ConvertHelp.obj2Double(xy[], );
    double y = ConvertHelp.obj2Double(xy[], );
    poin[i].X = (int)(x * );
    poin[i].Y = (int)(y * );
}

IntPtr orginRgn = IntPtr.Zero;
orginRgn = CreatePolygonRgn(poin, poin.Count(), );

比较两个多边形

先引用dll

    /// <summary>
        /*
         * CombineRgn(
              p1: HRGN;     {合成后的区域}
              p2, p3: HRGN; {两个原始区域}
              p4: Integer   {合并选项; 见下表}
            ): Integer;     {有四种可能的返回值}

            //合并选项:
            RGN_AND  = 1;
            RGN_OR   = 2;
            RGN_XOR  = 3;
            RGN_DIFF = 4;
            RGN_COPY = 5; {复制第一个区域}

            //返回值:
            ERROR         = 0; {错误}
            NULLREGION    = 1; {空区域}
            SIMPLEREGION  = 2; {单矩形区域}
            COMPLEXREGION = 3; {多矩形区域}
         */
        /// </summary>
        /// <param name="dest"></param>
        /// <param name="src1"></param>
        /// <param name="src2"></param>
        /// <param name="flags"></param>
        /// <returns></returns>
        [DllImport("gdi32.dll", CharSet = CharSet.Auto)]
        public static extern int CombineRgn(IntPtr dest, IntPtr src1, IntPtr src2, int flags);

使用起来就很简单，提供3个参数，第一个参数是合并后返回的句柄，第2个参数是多边形1号，第3个参数是多边形2号，最后一个flag参数是合并选项，1是and，2是or根据情况选用，这里选用And所以是1

返回结果0表示错误也就是没有交集，1表示空区域即无交集，2和3都表示有交集存在。

int nMix = CombineRgn(nextRgn, orginRgn, nextRgn, );
if (nMix !=  && nMix != )
{
    //有交集
}                    

获取交集的数据

计算交集的面积，其实就是如何根据句柄读取内存里的数据，因为网上大多数都是C++的写法，很少能找到。Net的写法，所以这个部分占用了我一下午时间，包括走了一些弯路 ，最后通过google才找到了正解。

先引用dll，根据API返回的数据结构建立对应的结构

        public struct RGNDATAHEADER
        {
            public int dwSize;
            public int iType;
            public int nCount;
            public int nRgnSize;
            public RECT rcBound;
        }

        public struct RECT
        {
            public int Left;
            public int Top;
            public int Right;
            public int Bottom;
        }
        /// <summary>
        /// 获取数据参考：http://www.pinvoke.net/default.aspx/gdi32/GetRegionData.html
        /// 数据结构参考：http://www.cnblogs.com/del/archive/2008/05/20/1203446.html
        /// </summary>
        /// <param name="hRgn"></param>
        /// <param name="size"></param>
        /// <param name="lpRgnData"></param>
        /// <returns></returns>
        [DllImport("gdi32.dll", CharSet = CharSet.Auto, SetLastError = true, ExactSpelling = true)]
        public static extern int GetRegionData(HandleRef hRgn, int size, IntPtr lpRgnData);

下面的代码只讲一下GetRegionData这个API的调用的特殊之处，首先他要调用2次才能正确获取到数据。

第一次调用如下GetRegionData(hr, 0, IntPtr.Zero)，传递一个空句柄，此时会返回一个int的值，告诉你需要准备一个多大的内存区域。

然后要申请一个内存区域准备去接值。IntPtr bytes = Marshal.AllocCoTaskMem(dataSize);就是准备一个特定大小的内存区域的句柄。

第二次调用GetRegionData(hr, dataSize, bytes)的时候就能把我们想要的数据填充到bytes这个句柄指向的内存区域了。

接下来的问题就是有了句柄如何取结构化的数据了，C#里支持指针操作，但是是unsafe的代码。最关键一句话在下面已经加了注释 了。

	const int RDH_RECTANGLES = 1;

        /// <summary>
        /// 分割多边形，获取多边形内所有的矩形
        /// </summary>
        /// <param name="hRgn"></param>
        /// <returns></returns>
        public unsafe static RECT[] RectsFromRegion(IntPtr hRgn)
        {
            RECT[] rects = null;
            var hr = new HandleRef(null, hRgn);
            // First we call GetRegionData() with a null buffer.
            // The return from this call should be the size of buffer
            // we need to allocate in order to receive the data.
            int dataSize = GetRegionData(hr, , IntPtr.Zero);

            if (dataSize != )
            {
                IntPtr bytes = IntPtr.Zero;

                // Allocate as much space as the GetRegionData call
                // said was needed
                bytes = Marshal.AllocCoTaskMem(dataSize);

                // Now, make the call again to actually get the data
                int retValue = GetRegionData(hr, dataSize, bytes);

                // From here on out, we have the data in a buffer, and we
                // just need to convert it into a form that is more useful
                // Since pointers are used, this whole routine is 'unsafe'
                // It's a small sacrifice to make in order to get this to work.
                // [RBS] Added missing second pointer identifier
                RGNDATAHEADER* header = (RGNDATAHEADER*)bytes;

                if (header->iType == RDH_RECTANGLES)
                {
                    rects = new RECT[header->nCount];

                    // The rectangle data follows the header, so we offset the specified
                    // header size and start reading rectangles.
                    //获取偏移
                    int rectOffset = header->dwSize;
                    for (int i = ; i < header->nCount; i++)
                    {
                        // simple assignment from the buffer to our array of rectangles
                        // will give us what we want.
                        //首先把bytes转换成指针，得到bytes的地址，然后加上偏移，再转换为RECT类型的指针。
                        rects[i] = *((RECT*)((byte*)bytes + rectOffset + (Marshal.SizeOf(typeof(RECT)) * i)));
                    }
                }

            }

            // Return the rectangles
            return rects;

        }

计算面积

因为上面获取到的数据其实是一个RECT的数组，而RECT里面包含的是上下左右四个点的坐标信息，那么很显然我们得到的是一个矩形的数组，每次分解大概有2000多个矩形，不用管多少了，直接拿来用就是了

        /// <summary>
        /// 计算多边形的面积
        /// </summary>
        /// <param name="rgn"></param>
        /// <returns></returns>
        public static int CalculateAreas(IntPtr rgn)
        {
            RECT[] rectData = RectsFromRegion(rgn);
            int ret = ;
            foreach (var rect in rectData)
            {
                int areas = (rect.Bottom - rect.Top) * (rect.Right - rect.Left);
                if (areas < )
                    areas = areas * -;
                ret += areas;
                //Console.WriteLine("{0},{1},{2},{3},{4}", rect.Top, rect.Left, rect.Right, rect.Bottom, areas);
            }
            return ret;
        }

总结

这次这个需求一开始以为不复杂，网上应该有现成的代码，实际上搜索后发现涉及的计算几何的知识对几何和算法的要求特别高，无奈几何知识都还给老师了，补习的话短短2-3天应该是来不及了。百度的能力毕竟有限，有的时候google能提供更大的帮助。通过另辟蹊径借用windowsAPI解决了这个问题，同时了解了C#在指针操作上的知识。