决策单调性&wqs二分

其实是一个还算 trivial 的知识点吧……早在 2019 年我就接触过了，然鹅当时由于没认真学并没有把自己学懂，故今复学之（

1. 决策单调性

引入：在求解 DP 问题的过程中我们常常遇到这样的问题：我们列出了一个 \(dp\) 状态转移方程式形如 \(dp_i=\min\limits_{j<i}dp_j+w(j+1,i)\) 或类似的形式，暴力转移时间复杂度 \(\mathcal O(n^2)\) 过不去，但是你发现这里的代价函数 \(w(l,r)\) 有一些比较好的性质，譬如单调性或凹凸性等，此时你可以考虑使用决策单调性优化 \(dp\)。

决策单调性，说白了就是假设 \(dp_i\) 从 \(dp_{from_i}\) 转移来，那么如果 \(from\) 数组满足 \(\forall j<i,from_j\le from_i\)，就称此处的 \(dp\) 满足决策单调性（当然有可能 \(dp_i\) 从多个 \(dp_j\) 转移过来都是最优的，此时决策单调性的定义就是存在一个 \(j\) 的最优决策点 \(\le\) 某个 \(i\) 的最优决策点）。

那么问题就来了，如果仅仅通过打表找规律的方法列出决策点那显然费时费力，有没有不失去一般性和快捷性的判定方法呢？

注：下文中若无特殊说明，默认为最小化问题，若为最大化问题一般都要将不等号方向反过来。

判定决策单调性的强有力工具：四边形不等式

四边形不等式，说白了就是如果对于任意四个满足 \(a\le b\le c\le d\) 的位置 \(a,b,c,d\)，都有 \(w(a,c)+w(b,d)\le w(a,d)+w(b,c)\)（当然如果是最大化问题则要将不等号方向反过来，可以简单记为“相交优于包含”），那么对应的 \(dp\) 数组则满足决策单调性。

证明：考虑反证法，假设存在某个 \(y<x\) 满足 \(from_x<from_y\)。方便起见下文中令 \(fx=from_x,fy=from_y\)。

那么根据 \(from\) 数组的定义显然有 \(dp_{fx}+w(fx+1,x)<dp_{fy}+w(fy+1,x)\ \ \ \ \ (1)\)

由于 \(fx+1<fy+1\le y<x\)，根据四边形不等式有 \(w(fx+1,y)+w(fy+1,x)\le w(fx+1,x)+w(fy+1,y)\ \ \ \ (2)\)

\((1)+(2)\)，整理得 \(dp_{fx}+w(fx+1,y)<dp_{fy}+w(fy+1,y)\)，显然与最优决策点的定义相悖。

区间包含单调

对于任意 \(a\le b\le c\le d\)，都有 \(w(b,c)\le w(a,d)\)，则称 \(w\) 包含单调。

包含单调似乎不能直接用来证决策单调性，因此要配合一些东西食用。

一些推论

没错这东西还有一些推论。

推论 \(1\)：如果 \(w\) 函数满足 \(w(l+1,r)+w(l,r-1)\le w(l,r)+w(l+1,r-1)\)，那么 \(w\) 满足四边形不等式。

证明：将式子变形得到 \(w(l,r)-w(l,r-1)\ge w(l+1,r)-w(l+1,r-1)\)

推广可得 \(w(l,r)-w(l,r-1)\ge w(l+k,r)-w(l+k,r-1),k\in\mathbb{Z}^+,l+k\le r-1\)

移项可得 \(w(l,r)-w(l+k,r)\ge w(l,r-1)-w(l+k,r-1)\)

进一步推广可得 \(w(l,r)-w(l+k,r)\ge w(l,r-p)-w(l+k,r-p),p\in\mathbb{Z}^+,l+k\le r-p\)

移项可得 \(w(l,r-p)+w(l+k,r)\le w(l,r)+w(l+k,r-p)\)

记 \(a=l,b=l+k,c=r-p,d=r\)，那么上式即可写作 \(w(a,c)+w(b,d)\le w(a,d)+w(b,c)\)

推论 \(2\)：如果某个 \(dp\) 方程满足 \(dp_{i,j}=\min\limits_{k}(dp_{i,k}+dp_{k+1,j}+w(i,j))\)，且 \(w(i,j)\) 满足包含单调和四边形不等式，则 \(dp\) 数组也满足四边形不等式。

证明：对区间长度归纳，显然 \(a=b=c=d\) 时必然有 \(dp_{a,c}+dp_{b,d}\le dp_{a,d}+dp_{b,c}\)。

我们要证明对于某个 \(a\le b\le c\le d\)，其中 \(a\ne d\)，有 \(dp_{a,c}+dp_{b,d}\le dp_{a,d}+dp_{b,c}\)，考虑分情况讨论：

1. \(b=c\)，那么设 \(x\) 为 \(dp_{a,d}\) 最优决策点，不妨设 \(x\le b\)，对于另外一半镜像一下即可，那么

   \[\begin{aligned}
   &dp_{a,d}+dp_{b,c}\\
   =&dp_{a,x}+dp_{x+1,d}+w(a,d)\\
   \ge&dp_{a,x}+dp_{x+1,b}+dp_{b,d}+w(a,d)\\
   \ge&dp_{a,x}+dp_{x+1,b}+dp_{b,d}+w(a,b)\\
   \ge&dp_{a,b}+dp_{b,d}
   \end{aligned}
   \]

2. \(b\ne c\)，设 \(x\) 为 \(dp_{a,d}\) 的最优决策点，\(y\) 为 \(dp_{b,c}\) 的最优决策点，不妨设 \(x\le y\)，那么

   \[\begin{aligned}
   &dp_{a,d}+dp_{b,c}\\
   =&dp_{a,x}+dp_{x+1,d}+w(a,d)+dp_{b,y}+dp_{y+1,c}+w(b,c)\\
   =&dp_{a,x}+dp_{b,y}+(dp_{x+1,d}+dp_{y+1,c})+(w(a,d)+w(b,c))\\
   \ge&dp_{a,x}+dp_{b,y}+(dp_{x+1,c}+dp_{y+1,d})+(w(a,d)+w(b,c))&(\text{对}x+1,y+1,c,d\text{进行四边形不等式})\\
   \ge&dp_{a,x}+dp_{b,y}+(dp_{x+1,c}+dp_{y+1,d})+(w(a,c)+w(b,d))\\
   \ge&=dp_{a,c}+dp_{b,d}
   \end{aligned}
   \]

得证。

具体应用是可以优化区间 \(dp\)，有兴趣的可以自己去实现，反正我是没兴趣咯（大雾。

决策单调性的实现

讲了一车理论（fei）知识（hua），接下来谈谈决策单调性怎么实现。

I. 单峰+1D：单指针跳跃

如果一个 \(dp\) 转移方程满足对于所有 \(dp_i\) 都有在 \(from_i\) 左边的位置对 \(dp_i\) 的贡献随下标的增大而单调递减，在 \(from_i\) 右边的位置对 \(dp_i\) 的贡献随着下标的增大而增大，那么结合决策单调性可以用一个指针维护决策点，每次求解某个 \(dp_i\) 就指针不断向后跳直到下一个位置的贡献劣于当前位置为止。

时间复杂度线性。

例题？抱歉，由于这种情况应用不是太广泛，因此没有例题……

II. 每一层之间的 \(dp\) 没有影响：分治

这种情况的适用范围为：二维 \(dp\)，只有上一层向下一层转移，同一层之间不会转移。而且每一层中有决策单调性。

具体来说我们定义一个函数 solve(l,r,pl,pr) 表示当前处理区间 \([l,r]\)，该区间中所有位置的决策点都在 \([pl,pr]\) 中，记 \(mid=\lfloor\dfrac{l+r}{2}\rfloor\)，每次我们暴力枚举 \([pl,pr]\) 中的决策点更新 \(dp_{mid}\) 即可，我们假设决策点为 \(pos\)，那么我们继续执行 solve(l,mid-1,pl,pos),solve(mid+1,r,pos,pr) 即可，正确性显然，由于递归层数最多 \(\log n\)，每层跳跃长度总和 \(\mathcal O(n)\)，因此总复杂度 \(\mathcal O(n\log n)\)。

有时候我们还会遇到这样的问题：代价函数 \(w(l,r)\) 不好直接求，但利用类似于莫队这种移指针的方式可以求得，譬如区间数颜色，此时也可以通过这种方式计算代价函数，由于每次移动左右端点都在候选区间中移，因此指针的移动次数也是 \(\mathcal O(n\log n)\) 的。

例题：

1. CF868F Yet Another Minimization Problem

模板题，记 \(w(l,r)\) 表示 \([l,r]\) 中相同数字的对数，那么显然有 \(w(l,r-1)+w(l+1,r)\le w(l,r)+w(l+1,r-1)\)，且等号不成立当且仅当 \(a_l=a_r\)，因此该 \(dp\) 是满足决策单调性的，又因为同一层之间的 \(dp\) 互不影响，因此可以使用分治优化，复杂度 \(n\log n\)。

const int MAXN=1e5;
const int MAXK=20;
int n,k,a[MAXN+5];ll dp[MAXN+5][MAXK+3];
int cl=1,cr=0,buc[MAXN+5];ll sum=0;
void push(int x){sum-=1ll*buc[a[x]]*(buc[a[x]]-1)>>1;buc[a[x]]++;sum+=1ll*buc[a[x]]*(buc[a[x]]-1)>>1;}
void pop(int x){sum-=1ll*buc[a[x]]*(buc[a[x]]-1)>>1;buc[a[x]]--;sum+=1ll*buc[a[x]]*(buc[a[x]]-1)>>1;}
ll calc(int l,int r){
	while(cr<r) push(++cr);
	while(cl>l) push(--cl);
	while(cl<l) pop(cl++);
	while(cr>r) pop(cr--);
	return sum;
}
void solve(int l,int r,int pl,int pr,int j){
	if(l>r||pl>pr) return;int mid=l+r>>1,pos=-1;
	for(int i=pl;i<=min(mid-1,pr);i++){
		if(dp[mid][j]>dp[i][j-1]+calc(i+1,mid))
			dp[mid][j]=dp[i][j-1]+calc(i+1,mid),pos=i;
	} solve(l,mid-1,pl,pos,j);solve(mid+1,r,pos,pr,j);
}
int main(){
	scanf("%d%d",&n,&k);memset(dp,63,sizeof(dp));dp[0][0]=0;
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	for(int i=1;i<=k;i++) solve(1,n,0,n,i);
	printf("%lld\n",dp[n][k]);
	return 0;
}

2. P5574 [CmdOI2019]任务分配问题

和上面差不多，只不过移指针时要用树状数组统计答案，因此时间复杂度 \(n\log^2n\)

3. LOJ #6039. 「雅礼集训 2017 Day5」珠宝

首先注意到每件物品的代价很小，最多只有 \(300\)，因此可以考虑在代价上做点文章，记 \(dp_{i,j}\) 表示考虑了代价 \(\le i\) 的物品，总代价 \(\le j\) 的最大价值，再记 \(mx_{i,j}\) 表示代价为 \(i\) 的物品中价值最大的 \(j\) 个物品价值之和，那么显然有 \(dp_{i,j}=\max\limits_{j-ki\ge 0}dp_{i-1,j-ki}+mx_{i,k}\)，注意到 \(mx_{i,k}\) 为下凸函数，因此该 \(dp\) 转移方程满足四边形不等式，在同一个剩余类（\(\bmod i\) 的同余系）中满足决策单调性，对每个剩余类分治一下即可。

真·\(10^7\log 10^7\) 给艹过去了

4. P2605 [ZJOI2010]基站选址

此题正解似乎不是什么决策单调性，但貌似决策单调性能水过去

首先考虑求出每个村庄，要使它不交补偿费，显然必须在某个区间中需有基站，我们假设这个区间为 \([L_i,R_i]\)，那么代价函数 \(w(l,r)\) 的定义即为 \(\sum\limits_{i=l}^rw_i[L_i>l][R_i<r]\)，不难发现它满足四边形不等式，即 \(w(l,r)+w(l+1,r-1)\ge w(l+1,r)+w(l,r-1)\)，分治+决策单调性优化即可，统计答案可用莫队的思想，加入左/右端点时在对应 vector 里 lower_bound 即可，理论复杂度 \(\mathcal O(nk\log^2n)\)，被正解碾压，但实际跑起来飞快，吊打部分实现不好的正经写法。

III. 1D1D：二分队列

适用范围：\(dp_i=\min\limits_{j<i}dp_j+w(j+1,i)\)。

大概就是，如果某个 \(dp\) 状态满足决策单调性，那么对于某两个可以转移到 \(i\) 的决策点 \(j,k(j<k)\)，如果 \(j\) 没有 \(k\) 来得优，那么随着 \(i\) 的增大，\(j\) 肯定更没有 \(k\) 来得优，此时 \(j\) 就没有用了。那么考虑以 \(i\) 的增大为时间线，某个决策点 \(j\) 从出生到被干掉的命运显然应该是这样的：开始时不如某些在它前面的决策点，后来不断变强，逐渐干掉在它前面的决策点并（有可能）成为最优决策点，在最优决策点保持一段时间后又被它后面的决策点反超。因此考虑维护一个单调队列，从队首到队尾决策点下标单调递增，同时对 \(i\) 的贡献单调递减，那么显然队首元素就是 \(i\) 的最优决策点。当 \(i\) 变为 \(i+1\) 时我们就不断弹出队首，直到队首元素由于队列第二个元素即可，将某个决策点 \(i\) 加入队列时，我们就记 \(need(x,y)\) 表示 \(x\) 最早什么时候能够比 \(y\) nb，那么我们比较 \(need(q[tl],q[tl-1])\) 与 \(need(i,q[tl])\)，如果 \(i\) 能比 \(q[tl]\) 干掉 \(q[tl-1]\) 更早地干掉 \(q[tl]\)，那么 \(q[tl]\) 显然就是个废物，弹出队列即可。\(need(x,y)\) 显然可以二分求出。

时间复杂度 \(n\log n\)。

5. P1912 [NOI2009] 诗人小G

裸的决策单调性优化 \(dp\)，打表可以发现代价函数 \(w\) 满足四边形不等式，而状态转移方程又满足 1D1D，因此可以使用二分队列优化，复杂度 \(n\log n\)，注意手写快速幂并使用 long double 避免精度问题！！！

6. P3515 [POI2011]Lightning Conductor

首先式子可以转化为 \(p\ge a_j-a_i+\sqrt{|i-j|}\)，因此我们只需求出 \(f_i=\max\limits_{j}a_j+\sqrt{|i-j|}\)，对于 \(j<i\) 和 \(j>i\) 两部分显然是对称的，因此我们只用着眼于一边即可，注意到这个 \(w(j,i)=\sqrt{|i-j|}\) 满足四边形不等式，因为 \(f(x)=\sqrt{x}\) 为上凸函数，二阶导数恒为负，因此可以决策单调性优化，上个决策单调性即可。

const int MAXN=5e5;
int n,a[MAXN+5],q[MAXN+5];
double dp1[MAXN+5],dp2[MAXN+5];
double rt[MAXN+5];
double calc(int x,int y){return a[x]+rt[y-x];}
int need(int x,int y){
	int l=x,r=n,p=n+1;
	while(l<=r){
		int mid=l+r>>1;
		if(calc(x,mid)>calc(y,mid)) p=mid,r=mid-1;
		else l=mid+1;
	} return p;
}
void solve(double *dp){
	int hd=1,tl=0;
	for(int i=1;i<=n;i++){
		while(hd<tl&&need(i,q[tl])<=need(q[tl],q[tl-1])) --tl;
		q[++tl]=i;
		while(hd<tl&&calc(q[hd],i)<calc(q[hd+1],i)) ++hd;
		dp[i]=calc(q[hd],i);
	}
}
int main(){
	scanf("%d",&n);for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	for(int i=1;i<=n;i++) rt[i]=sqrt(i);
	solve(dp1);reverse(a+1,a+n+1);solve(dp2);reverse(a+1,a+n+1);
	for(int i=1;i<=n;i++) printf("%d\n",max((int)(ceil(max(dp1[i],dp2[n-i+1])))-a[i],0));
	return 0;
}

IV. 二维：记录决策点

适用范围：二维 \(dp\)，满足决策单调性。

假设 \(dp_{i,j}\) 的决策点 \(from_{i,j}\) 随着 \(j\) 的增大而增大，也随着 \(i\) 的增大而增大，那么不难发现不等式 \(from_{i,j-1}\le from_{i,j}\le from_{i+1,j}\) 一定成立，因此我们正序枚举 \(j\)，倒序枚举 \(i\)，然后在对应区间内转移即可，显然复杂度是严格平方的，因为如果我们把 \(dp\) 看作一个矩形，那么矩形每条对角线上的决策点都是依次递增的，枚举次数自然也是 \(\mathcal O(n)\) 的，而对角线个数 \(\mathcal O(n)\)，因此总复杂度平方。

7. CF321E Ciel and Gondolas

设 \(dp_{i,j}\) 表示前 \(i\) 个人划分成 \(j\) 段的最小代价，那么显然代价函数 \(w(l,r)\) 满足决策单调性，记录转移点转移即可，转移时就求个二维前缀和，复杂度严格平方。

using namespace fastio;
const int MAXN=4000;
const int MAXK=800;
int n,k,a[MAXN+5][MAXN+5],s[MAXN+5][MAXN+5];
int dp[MAXN+5][MAXK+5],from[MAXN+5][MAXK+5];
int sum(int l1,int r1,int l2,int r2){
	return s[r1][r2]-s[l1-1][r2]-s[r1][l2-1]+s[l1-1][l2-1];
}
int main(){
	read(n);read(k);
	for(int i=1;i<=n;i++) for(int j=1;j<=n;j++){
		read(a[i][j]);s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];
	} memset(dp,63,sizeof(dp));dp[0][0]=0;
	for(int i=1;i<=k;i++) for(int j=n;j;j--)
		for(int l=from[j][i-1];l<=((j==n)?n:from[j+1][i]);l++)
			if(l<j&&dp[j][i]>dp[l][i-1]+sum(l+1,j,l+1,j))
				dp[j][i]=dp[l][i-1]+sum(l+1,j,l+1,j),from[j][i]=l;
	printf("%d\n",dp[n][k]>>1);
	return 0;
}

8. P4767 [IOI2000]邮局

同上，唯一的区别是代价函数的计算方式不同&输入格式不同（大雾）

9. P5897 [IOI2013]wombats

nb tea，线段树分块+决策单调性优化 dp，题解

参考资料：

• DP的四边形不等式及决策单调性优化

• DP的决策单调性优化总结，cmd_blk yyds！

2. wqs 二分

基本思想

似乎跟决策单调性关系不算太大，但是与决策单调性一样都属于通过观察 \(dp\) 数组的性质来优化 \(dp\)，因此就在这里一并讲掉了（

引入：给定一个由正整数组成的序列 \(a\)，你可以把它分成 \(k\) 段，使每段和的平方之和最小。

我会暴力 \(dp\)！\(dp_{i,j}\) 表示前 \(i\) 个数分成 \(j\) 段的最小代价，复杂度 \(n^3\)！

太慢了！有没有快一点的做法？

我会决策单调性优化 \(dp\)！这东西的代价函数满足四边形不等式，可以分治优化，复杂度 \(nk\log n\)！

还是慢了！有没有再快一点的做法？

我会斜率优化！这东西可以写成一次函数的形式，斜率优化一下可以到 \(\mathcal O(nk)\)！

能不能再快一点！

………………

这时候我们的 wqs 二分就要派上用场了。wqs 二分，又称忘情水王钦石二分，带权二分，DP 凸优化，常见于限制选取物品个数的 DP 当中（或者限制划分成 \(k\) 段），如果我们发现 \(dp_i\) 满足凹凸性（上凸/下凸），那么就可以考虑 wqs 二分。

关于 wqs 二分一个比较感性的认识是，以刚才的例子为例，如果我们不限制段数，那么根据 \((\sum\limits_{i=1}^na_i)^2\ge\sum\limits_{i=1}^na_i^2\) 可知我们肯定会贪心地选择每个元素单独一段，这样可能不满足 \(k\) 的限制，因此我们考虑加上一个额外的条件：每多分一段就可以 \(-c\) 的代价，那么显然如果 \(c\) 趋近于 \(\infty\) 我们就每个元素自己单独成一段了，而 \(c=0\) 就是之前的情形，那么我们能不能找到一个分界点，使得在上述情形中最优方案刚好分了 \(k\) 段呢？答案是肯定的，这就是 wqs 二分的基本思想。因此如果做题拿不准是否是 wqs 二分可以用该方法感性地判断，或者实在不行打个表观察一下也行。

感性的认识讲完了，下面讲理性的理解，还是以上面的例子为例，下面简记 \(f(x)\) 表示上面的 \(dp_{n,x}\)，打个表发现 \(f(x)\) 是个凸函数，因此考虑二分一个斜率 \(c\) 并用斜率为 \(-c\) 的直线去截这个凸包，那么该直线一定会卡到凸包下方的某个点，这个点显然一定是在 \(y\) 轴上截距最小的点——或者说，就是上面感性认识中，我们给每段代价 \(-c\) 后最优划分方案，我们考虑求出这个最优划分方案——这个就可以按照上面暴力做法那样决策单调性/斜率优化了，同时我们记录最优方案划分的段数 \(p\)，如果 \(p=k\) 那显然本题就做完了，答案就是 \(\text{最优划分策略的答案}+kc\)，否则如果 \(p>k\) 那我们就将 \(c\) 调大一点，如果 \(p<k\) 就将 \(c\) 调小一点，这样本题就做完了，复杂度 \(n\log n/n\log^2n\)，吊打上面的三个做法。

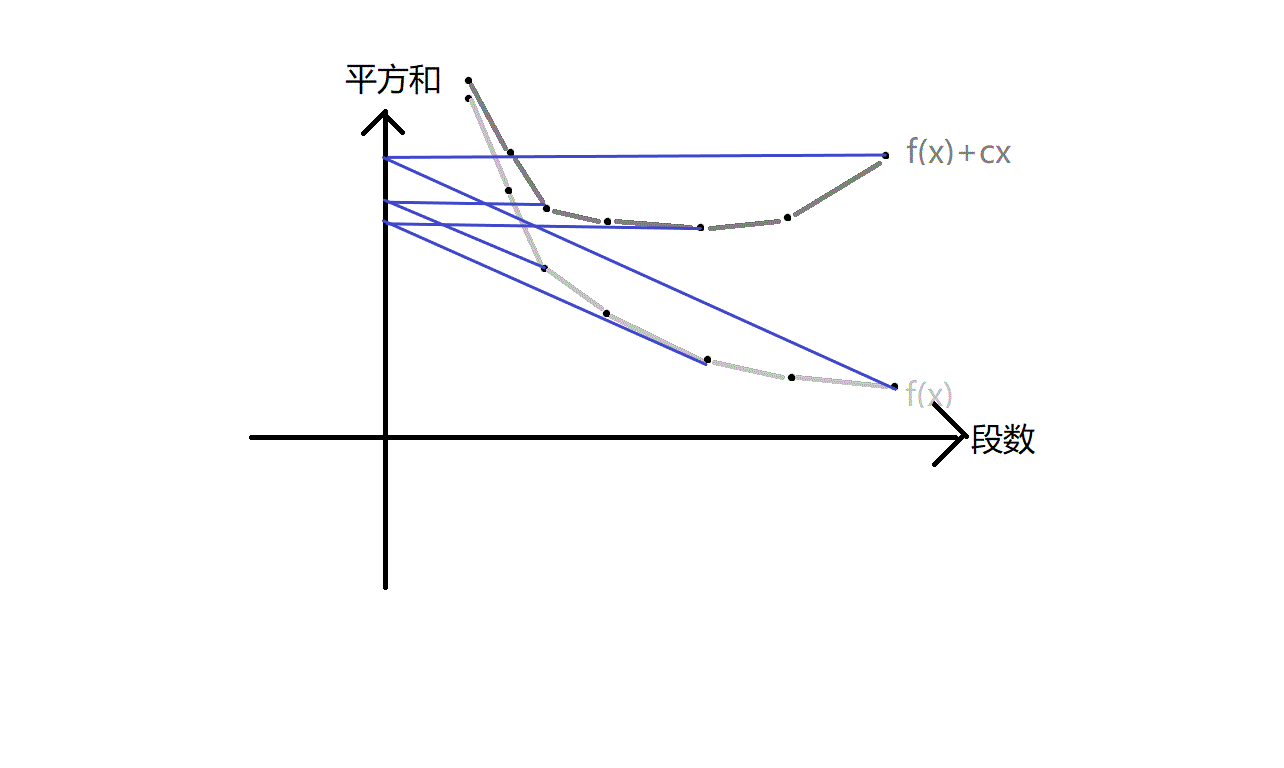
重要实现细节：三点共线

上述做法梦想很美满，现实很骨感，你照着上面的思路写，过了样例，一交……

WA……WA？WA！

原因是因为你没有特殊判断下面的情形：

在上面的情形中，假如我们的 \(k\) 刚好就是 \(C\) 点的横坐标，那么在 \(c\) 稍微大一点的情况下会切到 \(B\)（即上图中的橙色直线 \(k_1\)），\(c\) 稍微小一点的情况下会切到 \(D\)（即上图中的粉色线段），永远也轮不到 \(C\)，所以上面的状态还有待改进，我们考虑在最优答案相同时，保留划分段数最大的答案，然后如果划分段数 \(\ge k\) 就更新答案，并且更新答案为最终最优解 \(+k\times mid\)，而不是最优解 \(+\text{最优划分段数}\times k\)。为什么要限制这个划分段数最大/最小呢，因为显然直线在切到 \(B\) 和切到 \(D\) 之间总会有一个斜率的分界点对吧，我们的答案肯定会取分界点左边减去一个很小的值 \(\epsilon\) 对吧，那由于它大于真正的 \(BD\) 之间的斜率 \(k\)，因此它总会切到 \(D\)，但由于它与真正的分界点之间的差太微小了，我们的程序会把它与 \(B\) 处的答案认作同一个值，那么怎么办呢……这时候就要以划分段数为第二关键字了，如果我们没有这个操作那切到 \(B\) 时候答案就不会被更新了，这显然是我们所不希望的，加上这个操作就可以避免这个 error 了。当然你也可以保留划分段数最小的答案，那么此时就要在划分段数 \(\le k\) 时更新答案，这样就可以过了。

其他细节

• 在 wqs 二分中，由于 \(dp\) 值一般是整数，因此斜率 \(c=\dfrac{dp_{i+1}-dp_i}{i+1-i}=dp_{i+1}-dp_i\) 也是整数，因此二分可以不用实数域上二分，但如果碰到小数的 \(dp\) 值就要实数域二分了。
• 可以将 \((\text{代价},\text{划分段数})\) 封成一个类，手动重载小于号和加号，这样可以省去不少繁琐的比较操作，但可能常数会有亿点大（因为加了类封装后常数本来就会变大）

wqs 二分与费用流的关系

众所周知，

如果是一个费用流模型，它肯定具有下凸性。

因为费用流的过程中，肯定是先增广最短路，增广完了之后不可能增广更短的路。

——某位我不认识的神仙

说人话，就是假设我们每次增广流量为 \(1\) 的流，那么显然每次增广时我们会选择一条 \(S\to T\) 的最短路径，并令答案加上这条路径的权值之和，由于增广之后会减少正向边的权值，因此对于一条 \(S\to T\) 的路径，如果我们第 \(k\) 次增广时增广了它，那么显然 \(\forall i\in[1,k-1]\)，第 \(i\) 次增广时这条路径也在图上，因此第 \(i\) 次增广的权值 \(g(i)\) 是一个递增函数，前 \(i\) 次增广的路径之和 \(f(i)\) 自然就是一个下凸函数。所以如果多次增广的费用流问题，我们可以用 wqs 二分来优化。

例题

10. P2619 [国家集训队]Tree I

记 \(f_i\) 为选 \(i\) 条白边的答案，那么我们感性理解一下，如果我们给每条白边权值 \(-\infty\)，那么显然选择的白边条数会取到最大值；如果给它们都加上 \(\infty\)，那么选择的白边条数会取到最小值——也就是说存在一个分界点 \(c\) 使得给每条白边权值 \(-c\) 后最小生成树中恰好有 \(k\) 条白边，故 \(f_i\) 为凸函数，wqs 二分即可，复杂度 \(n\log^2n\)，可以使用归并排序，即将黑边白边在预处理时分别排序，每次二分时归并一下即可，配合路径压缩+启发式合并可以做到 \(\mathcal O(n\alpha(n)\log n)\)，没有兴趣实现……

const int MAXN=5e4;
const int MAXM=1e5;
int n,m,need,ans;
struct edge{
	int u,v,w,col;
	bool operator <(const edge &rhs){
		return (w^rhs.w)?(w<rhs.w):(col<rhs.col);
	}
} e[MAXM+5];
int f[MAXN+5];
int find(int x){return (!f[x])?x:f[x]=find(f[x]);}
bool check(int mid){
	for(int i=1;i<=n;i++) f[i]=0;
	for(int i=1;i<=m;i++) if(!e[i].col) e[i].w-=mid;
	sort(e+1,e+m+1);int tot=0,res=0;
	for(int i=1;i<=m;i++){
		int fu=find(e[i].u),fv=find(e[i].v);
		if(fu==fv) continue;f[fu]=fv;
		tot+=!e[i].col;res+=e[i].w;
	} for(int i=1;i<=m;i++) if(!e[i].col) e[i].w+=mid;
	return (tot>=need)?(ans=res+mid*need,1):0;
}
int main(){
	scanf("%d%d%d",&n,&m,&need);
	for(int i=1;i<=m;i++){
		scanf("%d%d%d%d",&e[i].u,&e[i].v,&e[i].w,&e[i].col);
		++e[i].u;++e[i].v;
	} int l=-100,r=100,p=0;
	while(l<=r){
		int mid=l+r>>1;
		if(check(mid)) p=mid,r=mid-1;
		else l=mid+1;
	} printf("%d\n",ans);
	return 0;
}

11. CF739E Gosha is hunting

首先三方的 \(dp\) 显然：\(dp_{i,a,b}\) 表示取前 \(i\) 个球的过程中中用了 \(a\) 个宝贝球和 \(b\) 个超级球的最小代价，显然可以 wqs 二分，于是上个 wqs 二分找最优划分段数为 \(B\) 的斜率即可，时间复杂度平方对数，可以通过 wqs 二分套 wqs 二分做到 \(n\log^2n\)，有兴趣的可以自己去实现一下，反正我是从来没有兴趣咯……

通过以下代码了解一下决策单调性 \(dp\) 数组的类如何实现：

const int MAXN=2000;
const double EPS=1e-12;
int n,x,y;double a[MAXN+5],b[MAXN+5],ans=0;
struct dp_val{
	int num;double res;
	dp_val(int _num=0,double _res=0):num(_num),res(_res){}
	bool operator <(dp_val rhs) const{
		return (fabs(res-rhs.res)<EPS)?(num>rhs.num):(res<rhs.res);
	}
	dp_val operator +(dp_val rhs) const{
		return dp_val(num+rhs.num,res+rhs.res);
	}
} dp[MAXN+5][MAXN+5];
int main(){
	scanf("%d%d%d",&n,&x,&y);
	for(int i=1;i<=n;i++) scanf("%lf",&a[i]);
	for(int i=1;i<=n;i++) scanf("%lf",&b[i]);
	double l=0,r=1;
	while(fabs(r-l)>EPS){
		double mid=1.0*(l+r)/2;
		for(int i=1;i<=n;i++) for(int j=0;j<=y;j++) dp[i][j]=dp_val();
		for(int i=1;i<=n;i++) for(int j=0;j<=y;j++){
			chkmax(dp[i][j],dp[i-1][j]+dp_val(0,0));
			chkmax(dp[i][j],dp[i-1][j]+dp_val(1,a[i]-mid));
			if(j){
				chkmax(dp[i][j],dp[i-1][j-1]+dp_val(0,b[i]));
				chkmax(dp[i][j],dp[i-1][j-1]+dp_val(1,a[i]+b[i]-a[i]*b[i]-mid));
			}
		} dp_val mx;
		for(int j=0;j<=y;j++) chkmax(mx,dp[n][j]);
		if(mx.num<=x) r=mid,ans=mx.res+x*mid;
		else l=mid;
	} printf("%.10lf\n",ans);
	return 0;
}

此外，此题还可以使用费用流求解：新建两个点 \(A,B\)，从 \(S\) 向 \(A\) 连容量 \(a\) 权值 \(0\) 的边，向 \(B\) 连容量 \(b\) 权值 \(0\) 的边，从 \(A\) 向每个球 \(i\) 连容 \(1\) 权值 \(p_i\) 的边；从 \(B\) 向每个球连容 \(1\) 权值 \(u_i\) 的边，然后从 \(i\) 向 \(T\) 连两条边，容量均为 \(1\)，一条权值 \(0\)，一条权值 \(-u_ip_i\)，然后跑最大费用最大流即可。

12. P4383 [八省联考2018]林克卡特树

首先题目等价于选择 \(k+1\) 条不同的链，问它们边权之和的最大值，打个表可以发现该 \(dp\) 为凸函数，因此可以 wqs 二分。

二分一个斜率 \(k\)，然后设 \(dp_{u,0/1/2}\) 表示考虑了 \(u\) 的子树，\(u\) 下方连了 \(0/1/2\) 条边的最大权值之和，再设 \(f_u\) 表示以 \(u\) 为根的子树中，与 \(u\) 的父亲不连边时的答案。转移就枚举对应的儿子的状态合并一下即可，具体来说转移方程如下（其中 \(w\) 为 \((u,v)\) 边的权值）：

• \(dp_{u,2}=\max\{dp_{u,2},dp_{u,1}+dp_{v,1}+w-mid,dp_{u,1}+f_{v}\}\)
• \(dp_{u,1}=\max\{dp_{u,1},dp_{u,0}+dp_{v,1}+w-mid,dp_{u,0}+f_v\}\)
• \(dp_{u,0}=dp_{u,0}+dp_{v,0}\)

最后 \(f_u=\max\{dp_{u,0},dp_{u,1}-mid,dp_{u,2}\}\)

注意转移顺序，应按照 \(2\to 1\to 0\) 的顺序转移，还有二分斜率有可能是负的，因此二分下界不能设为 \(0\)！！！！111

13. CF802O April Fools' Problem (hard)

并不是愚人节的题目（大雾

首先此题显然可以 wqs 二分否则我就不会把它放在这里了（London Fog

对于每一道题有三种选择：

1. 跳过它，不使用它
2. 把它当作一个准备的决策
3. 把它和之前最小的 \(a\) 匹配，并打印

我们可以用优先队列来维护这个过程，时间复杂度 \(n\log n\log w\)。

14. CF958E2 Guard Duty (medium)

还是按照套路 wqs 二分，然后二分内部是一个 dp，朴素 dp 是平方的，稍微用点脑子就知道可以使用前缀 \(\min\) 优化，复杂度 \(n\log n\)。

15. P4983 忘情

首先将题目中那个奇奇怪怪的贡献柿子拆开可得 \(w(l,r)=(1+\sum\limits_{i=l}^ra_i)^2\)，然后按照套路 wqs 二分即可，wqs 二分内部我们设 \(dp_i\) 表示划分前 \(i\) 个数的最小代价，那么有 \(dp_i=\sum\limits_{j<i}w(j+1,i)+dp_j\)，斜率优化即可，复杂度 \(n\log n\)。

16. P6246 [IOI2000] 邮局 加强版

没错就是 \(8\) 的加强版，不过学了 wqs 二分这个加强版和原题就没啥区别了……

上个 wqs 二分，然后决策单调性优化一下即可。

由于转移方程是 1D1D，因此需要二分队列

17. P5633 最小度限制生成树

如果把每个点的颜色看作它是否有一个端点为 \(s\)，那么就跟 \(10\) 一样了……

注意判 Impossible！

18. P5308 [COCI2019] Quiz

上凸壳写成下凸壳了都能过样例，就 nm 离谱

首先如果不考虑 \(k\) 的限制那么可以考虑倒着 \(dp\)，\(dp_i\) 表示还剩 \(i\) 个人最多能够获得的奖金，那么有 \(dp_i=\max\limits_{j<i}dp_j+\dfrac{i-j}{i}\)，发现这东西可以斜率优化，即对于 \(j<k\)，从 \(k\) 转移比从 \(j\) 转移更优的充要条件是 \(dp_j+\dfrac{i-j}{i}<dp_k+\dfrac{i-k}{i}\)，即 \(\dfrac{dp_j-dp_k}{j-k}>\dfrac{1}{i}\)，斜率优化一下即可。加个 \(k\) 的限制之后上个 wqs 即可。

19. P5617 [MtOI2019]不可视境界线 / 2021.7.14 六校联训 T2 / NFLSOJ #1055

真·昨天刚学的 wqs 二分今天就能在模拟赛中派上用场

傻逼卡精度+卡常屑题

首先一眼 wqs 二分，二分内部可以 \(dp\)，\(dp_i\) 表示前 \(i\) 个圆覆盖的并减去 \(mid\) 乘圆的个数的最大值，那么显然有转移方程 \(dp_i=\max\limits_{j<i}dp_j+w(j,i)-mid\)，其中 \(w(j,i)\) 是一个与 \(x_i-x_j\) 有关的函数，可以通过 cmath 库预处理出来，发现它是一个下凸函数，因此莽个决策单调性即可。

时间复杂度 \(n\log n\log w\)，然鹅由于涉及浮点数的运算，常数上天……

参考资料：

• DP 优化方法大杂烩
• wqs二分 学习笔记