【Matrix-tree Theorem学习笔记】

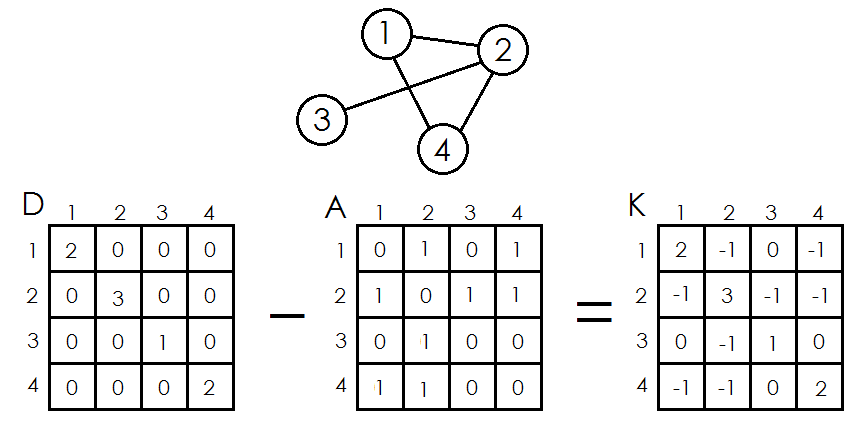
定义度数矩阵\(D(G)\)：

定义邻接矩阵\(C(G)\):

定义\(Laplace\)矩阵\(A\)

\(
A(G) = D(G) - C(G)
\)

记图\(G\)的所有生成树权值和为\(t(G)\)

一颗树形结构的权值为该树所有边权的积

无向图情况：

如果存在一条边\((x,y,w)\)

则\(D_{x,x},D_{y,y} += w\)

则\(C_{x,y},C_{y,x} += w\)

则\(A\)删除根节点对应的行和列，剩下的\(n - 1\)阶主子式则是权值之和

有向图情况：

如果存在一条边\((x,y,w)\)

如果统计根向树形图则\(D_{x,x} += w\)

如果统计外向树形图则\(D_{y,y} += w\)

两种情况都为

\(C_{x,y} += w\)

权设为\(1\)则可以统计生成树个数。

【模板】Matrix-Tree 定理

矩阵树

#include<iostream>
#include<cstdio>
#define ll long long
#define N 305
#define mod 1000000007
#define inv(x) (fpow(x,mod - 2))

ll n,m,typ;
ll a[N][N];

ll fpow(ll x,ll k){
	ll ans = 1;
	while(k){
		if(k & 1)
			ans = ans * x % mod;
		x = x * x % mod;
		k >>= 1;
	}
	return ans;
}

void del(int r){
	for(int i = 1;i <= n;++i)
	for(int j = 1;j <= n;++j){
		if(i != r && j != r){
			ll x = i > r ? i - 1 : i;
			ll y = j > r ? j - 1 : j;
			a[x][y] = a[i][j];
		}
	}
}

ll det(){
	ll ans = 1;
	for(int i = 1;i <= n;++i){
		if(!a[i][i]){
			for(int j = i + 1;j <= n;++j){
				if(a[j][i]){
					for(int k = 1;k <= n;++k)
					std::swap(a[i][k],a[j][k]);
					ans -= ans;
					break;
				}
			}
		}
		ll t = inv(a[i][i]);
		for(int j = i + 1;j <= n;++j){
			ll f = a[j][i] * t % mod;
			for(int k = i;k <= n;++k)
			a[j][k] = (a[j][k] - a[i][k] * f % mod) % mod;
		}
	}
	for(int i = 1;i <= n;++i)
	ans = ans * a[i][i] % mod;
	return (ans % mod + mod) % mod;
}

int main(){
	scanf("%lld%lld%lld",&n,&m,&typ);
	ll x,y,z;
	for(int i = 1;i <= m;++i){
		scanf("%lld%lld%lld",&x,&y,&z);
		if(x != y){
			if(typ == 0){
				a[x][x] = (a[x][x] + z) % mod,a[y][y] = (a[y][y] + z) % mod;
				a[x][y] = (a[x][y] - z) % mod,a[y][x] = (a[y][x] - z) % mod;
			}else{
				a[y][y] = (a[y][y] + z) % mod;
				a[x][y] = (a[x][y] - z) % mod;
			}
		}
	}
	del(1);
	n -= 1;
	std::cout<<det()<<std::endl;
}