20210716考试-NOIP16

考场时Prim的 $i$ 写成 $k$ 100->0 rank1->rank23

---

T1 Star Way To Heaven

考场正解：假设你要二分答案，则几个圆组成几道“屏障”把画面切成几部分，走每一个屏障的最长边的中点，这样是最优的。

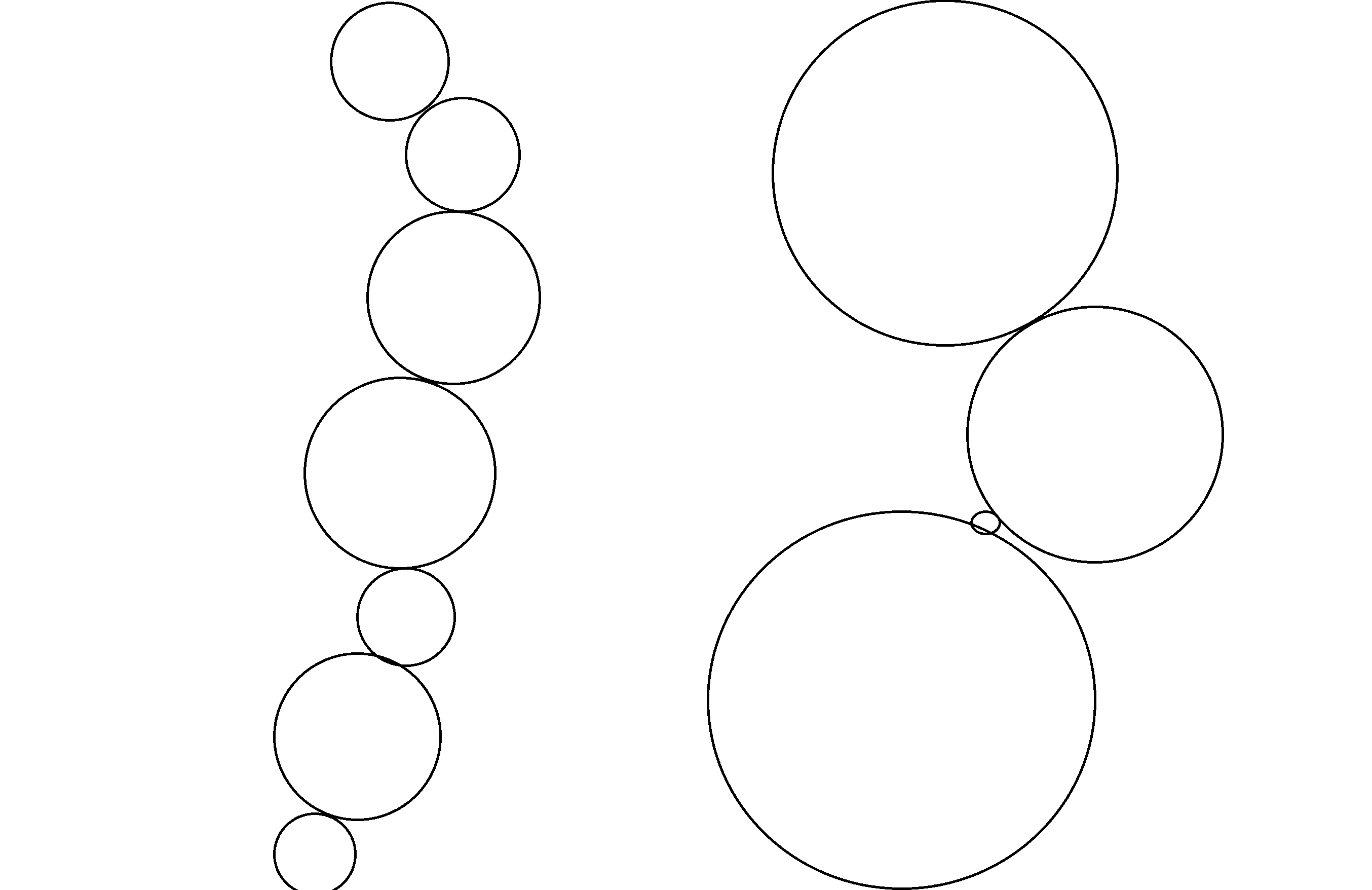
但是屏障间的点可能对答案有影响，所以要把它们合成为一道屏障。

首先取上或下边界，如集合，之后每次取离集合最近的点加入集合，这样就可以找到“屏障”合成后的样子，因为：

对于这样子的三个点，$d(1,2),d(2,3)<=d(1,3)$，所以对于题目而言，只使用 $d(1,2),d(2,3)$ 的距离就可以成功限制好对答案的影响。

在求出的点集中的边取最大值的一半即为答案。

#include<bits/stdc++.h>
using namespace std;
const int N=1100000,K=6100;
const long double INF=0x7fffffff;
inline int read()
{
    int s=0,w=1;char ch=getchar();
    while(!isdigit(ch)){if(ch=='-')w=-1;ch=getchar();}
    while(isdigit(ch)){s=s*10+ch-'0';ch=getchar();}
    return s*w;
}
int n,m,k;
bool vis[K];
long double x[K],y[K],ans,dis[K];
long double X(int q)
{
    return x[q];
}
long double Y(int q)
{
    return y[q];
}
long double D(int a,int b)
{
    return sqrt((X(a)-X(b))*(X(a)-X(b))+(Y(a)-Y(b))*(Y(a)-Y(b)));
}
int main()
{
    n=read();m=read();k=read();
    for(int i=1;i<=k;i++)
    {
        scanf("%Lf%Lf",&x[i],&y[i]);
    }
    for(int i=1;i<=k;i++)
    {
        dis[i]=1.0*y[i];
    }
    dis[k+1]=m;
    for(int i=1;i<=k+1;i++)
    {
        long double minn=INF;
        int x=-1;
        for(int j=1;j<=k+1;j++)
        {
            if(vis[j])
                continue;
            if(dis[j]<minn)
            {
                minn=dis[j];
                x=j;
            }
        }
        vis[x]=1;
        ans=max(dis[x],ans);
        if(x==k+1)
        {
            printf("%.8Lf\n",ans*0.5);
            return 0;
        }
        for(int j=1;j<=k;j++)
        {
            if(!vis[j])
            {
                dis[j]=min(dis[j],max(dis[x],D(x,j)));
            }
        }
        dis[k+1]=min(dis[k+1],m-y[x]);
    }
//    printf("%.8Lf\n",ans/2.0);
    return 0;
}
/*
10 5 2
1 1
2 3
*/

---

T2 God Knows

玄学DP，考场想50mins没想出 $n^2$ DP，写了一个只能过样例的假DP竟然有10分...

我对这个DP理解并不深，这篇博客更好。

\begin{align}
f[i]=\min f[j]+c[i] (j < i\And p[j] < p[i] \And \forall j< k < i , p[k] < p[j] || p[k] > p[i] )
\end{align}

f[i]表示前i个点已经被解决。

对这个式子的解释是：f[i]如果要从f[j]转移，则必须要保证 \([j+1,i]\) 内的点都与线 \(j\) 或线 \(i\) 相交，同时线 \(j\) 不能与线 \(i\) 相交。

对这个式子分析可以发现，从 \(1\) 到 \(n\) 的一个合法的转移序列中, \(p[i]\) 是递减的。即 \(p[i]\) 在 \(i\) 上递减。

或者说， \(i\) 在 \(p[i]\) 上递减。

那么可以以 \(p\) 维护一棵线段树，可以 \(O(\log(n))\) 查出合法最佳转移。

#include<bits/stdc++.h>
using namespace std;
const int N=210000,INF=0x7fffffff;
int nxt,n,p[N],w[N];
struct xds
{
    int l,r,mn,mx,upmn;
}t[N*4];
void build(int p,int l,int r){
    t[p].l=l; t[p].r=r;
    t[p].mn=t[p].upmn=INF;
    t[p].mx=-1;
    if(l==r) return ;
    int mid=(l+r)>>1;
    build(p*2,l,mid);
    build(p*2+1,mid+1,r);
}
int calc(int p,int nxt)
{
    if(t[p].l==t[p].r)
        return t[p].mx>nxt?t[p].mn:INF;
    if(t[p*2+1].mx>nxt)
        return min(t[p*2].upmn,calc(p*2+1,nxt));
    return calc(p*2,nxt);
}
int query(int p,int l,int r)
{
    int res=INF;
    if(t[p].l>=l&&t[p].r<=r)
    {
        res=calc(p,nxt);
        nxt=max(t[p].mx,nxt);
        return res;
    }
    if(r>=t[p*2+1].l)
        res=min(query(p*2+1,l,r),res);
    if(l<=t[p*2].r)
        res=min(query(p*2,l,r),res);
    return res;
}
void insert(int p,int pos,int tail,int val){
    if(t[p].l==t[p].r){
        t[p].mn=val;
        t[p].mx=tail;
        return ;
    }
    if(pos<=t[p*2].r) insert(p*2,pos,tail,val);
    else insert(p*2+1,pos,tail,val);
    t[p].mx=max(t[p*2].mx,t[p*2+1].mx);
    t[p].mn=min(t[p*2+1].mn,t[p*2].upmn=calc(p*2,t[p*2+1].mx));
}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        scanf("%d",&p[i]);
    for(int i=1;i<=n;i++)
        scanf("%d",&w[i]);
    n++;
    p[n]=n;
    build(1,0,n+1);
    insert(1,0,0,0);
    for(int i=1,ans;i<=n;i++)
    {
        nxt=-1;
        ans=query(1,0,p[i]-1)+w[i];
        insert(1,p[i],i,ans);
        if(i==n)
            printf("%d\n",ans);
    }
    return 0;
}

---

T3 Lost My Music



这题首测卡题面没说的精度，大家纷纷炸成10分。

考场暴力50分。

作如下变形：

\(\frac{c_v-c_u}{dis(u,v)}=-\frac{c_u-c_v}{dep_u-dep_v}\)

如果把 \(c\) 看成横坐标，\(dep\)看成纵坐标，题目变成了一个实时维护斜率最大值的题。

维护一个下凸包，树上 \(dfs\),用单调栈维护凸包，每到达一个点，二分出该点在凸包上的插入位置，这时栈顶斜率即为该点答案。

回溯时把凸包改回原来的样子。

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=1100000;
long double ans[N];
int dep[N],head[N],cnt,zhan[N];
int n;
ll c[N];
struct bian
{
    int nxt,to;
}b[N];
void add(int u,int v)
{
    b[++cnt].to=v;
    b[cnt].nxt=head[u];
    head[u]=cnt;
}
long double K(int x,int y)
{
    return (long double)(c[x]-c[y])/(long double)(dep[x]-dep[y]);
}
int get(int u,int r)
{
    int l=2,mid;
    long double k1,k2;
    while(l<=r)
    {
        mid=(l+r)>>1;
        k1=(long double)(-1)*K(zhan[mid],zhan[mid-1]);
        k2=(long double)(-1)*K(zhan[mid],u);
        if(k1<k2)
            r=mid-1;
        else
            l=mid+1;
    }
    return l-1;
}
void dfs(int u,int fa,int top)
{
    int k=get(u,top)+1,tmp1=zhan[k],tmp2=zhan[k-1];
    if(u==1)
        k=1;
    ans[u]=(long double)(-1)*K(tmp2,u);
    zhan[k]=u;
    for(int i=head[u],v;i;i=b[i].nxt)
    {
        v=b[i].to;
        if(v==fa)
            continue;
        dep[v]=dep[u]+1;
        dfs(v,u,k);
    }
    zhan[k]=tmp1;
}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%lld",&c[i]);
    }
    for(int i=2,a;i<=n;i++)
    {
        scanf("%d",&a);
        add(a,i);
    }
    dep[1]=1;
    dfs(1,0,0);
    for(int i=2;i<=n;i++)
    {
        printf("%.10Lf\n",ans[i]);
    }
    return 0;
}
/*
8
31516 11930 18726 12481 79550 63015 64275 7608
1 1 2 4 2 4 5
*/

---

这次考试用脚出题……

下发文件上写着第一题没有SPJ,第二题有，实际相反。

T1题面说输出一行整数……害了多少人以为是走整数点路径。

T3卡精度后来又重测。

T3数据说的 \(500\) 内数据也残缺。

上一次考试T1还出了超出100%数据范围的数据，巨佬cyh搞了1h才发现。