【luoguP5490】【模板】扫描线

求\(n\)个矩形的面积并，可以用线段树维护一条垂直于\(y\)轴的直线上被矩形覆盖的长度有多少长，将直线从左往右扫一遍，遇到矩形左边界就+1，遇到右边界就-1，不为\(0\)的位置就表示没有覆盖

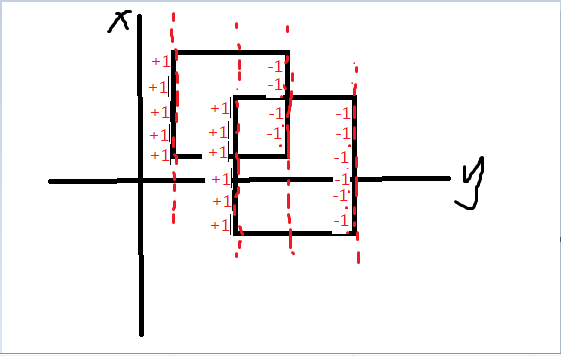
不为\(0\)的位置的多少似乎不好维护，

考虑这样一个性质:

如果一个线段树上的区间在扫过一个矩形的左边界被全部覆盖,那么在这个扫过矩形的右边界之前它都是全部被覆盖着的，并且我们每次询问都是询问[1,n]

我们可以在线段树上记录一个\(cnt\)表示一个区间被几个矩形完全覆盖了，如果cnt!=0，那么这个区间的\(ans=r-l\)，这样就不需要标记下传了

如果cnt==0，那么用左儿子的ans加上右儿子的ans就可以了

注意线段树左右合并时中间的长度没有计算，所以要用[l,r]的线段树结点维护[l,r+1]的区间

因为数据范围较大，需要离散化

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<map>
#define lc p<<1
#define rc p<<1|1
#define mid ((l+r)>>1)
using namespace std;

const int MAXN=100010;

inline int read(){
	int x=0; char c=getchar();
	while(c<'0') c=getchar();
	while(c>='0') x=x*10+c-'0',c=getchar();
	return x;
}

struct Matrix{
	int x1_,x2_,y1_,y2_;
} a[MAXN];

int n,xx[MAXN<<1],cnt;
int revx[MAXN<<1];

long long Ans;

map<int,int> mx;

struct Upd{
	int yid,l,r,k;
} u[MAXN<<1];

inline bool cmp(Upd p,Upd q){
	return p.yid<q.yid;
}

int len[MAXN<<4],Cnt[MAXN<<4],numx;

inline void push_up(int p,int l,int r){
	if(Cnt[p]){
		len[p]=revx[r+1]-revx[l];
		if(l!=r)
			cout<<len[p]<<' '<<len[lc]+len[rc]<<' '<<Cnt[lc]<<' '<<Cnt[rc]<<endl;
	}
	else len[p]=len[lc]+len[rc];
}

inline void update(int L,int R,int d,int p=1,int l=1,int r=numx){
	if(L<=l&&r<=R){
		Cnt[p]+=d;
		push_up(p,l,r);
		return;
	}
	if(L<=mid) update(L,R,d,lc,l,mid);
	if(R>mid) update(L,R,d,rc,mid+1,r);
	push_up(p,l,r);
}

signed main()
{
	n=read();
	for(int i=1;i<=n;++i){
		a[i].x1_=read(),a[i].y1_=read();
		a[i].x2_=read(),a[i].y2_=read();
		xx[++cnt]=a[i].x1_;
		xx[++cnt]=a[i].x2_;
	}
	sort(xx+1,xx+1+cnt);
	for(int i=1;i<=cnt;++i)
		if(xx[i]!=xx[i-1])
			mx[xx[i]]=++numx,revx[numx]=xx[i];
	int unum=0;
	for(int i=1;i<=n;++i){
		u[++unum].yid=a[i].y1_;
		u[unum].l=a[i].x1_;
		u[unum].r=a[i].x2_;
		u[unum].k=1;
		u[++unum].yid=a[i].y2_;
		u[unum].l=a[i].x1_;
		u[unum].r=a[i].x2_;
		u[unum].k=-1;
	}
	sort(u+1,u+1+unum,cmp);
	for(int i=1;i<=unum;++i){
		if(i>1&&u[i].yid!=u[i-1].yid){
			Ans+=1ll*len[1]*(u[i].yid-u[i-1].yid);
		}
		update(mx[u[i].l],mx[u[i].r]-1,u[i].k);
	}
	printf("%lld\n",Ans);
	return 0;
}