大数定律（Law of Large Numbers）
大数定律：每次从总体中随机抽取1个样本，这样抽取很多次后，样本的均值会趋近于总体的期望。也可以理解为：从总体中抽取容量为n的样本，样本容量n越大，样本的均值越趋近于总体的期望。当样本容量极大时，样本均值 。
（注：总体数据需要独立同分布）
下图展示的是：每次从1，2，3当中随机选取一个数字，随着抽样次数的增加，样本均值越来越趋近于总体期望（(1+2+3)/3=2）。
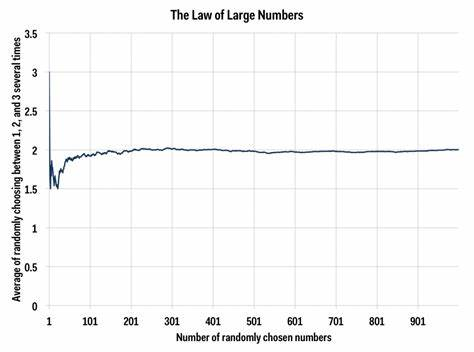
大数定律的作用：可以用样本均值来估计总体的期望。
大数定律（Law of Large Numbers）的更多相关文章
- 中心极限定理 | central limit theorem | 大数定律 | law of large numbers
每个大学教材上都会提到这个定理,枯燥地给出了定义和公式,并没有解释来龙去脉,导致大多数人望而生畏,并没有理解它的美. <女士品茶>有感 待续~ 参考:怎样理解和区分中心极限定理与大数定律?
- Law of large numbers and Central limit theorem
大数定律 Law of large numbers (LLN) 虽然名字是 Law,但其实是严格证明过的 Theorem weak law of large number (Khinchin's la ...
- 【概率论】6-2:大数定理(The Law of Large Numbers)
title: [概率论]6-2:大数定理(The Law of Large Numbers) categories: - Mathematic - Probability keywords: - Ma ...
- Markov and Chebyshev Inequalities and the Weak Law of Large Numbers
https://www.math.wustl.edu/~russw/f10.math493/chebyshev.pdf http://www.tkiryl.com/Probability/Chapte ...
- uva10392 Factoring Large Numbers
uva10392 Factoring Large Numbers 本文涉及的知识点是,使用线性筛选法得到素数表. Table of Contents 1 题目 2 思路 3 参考 1 题目 ===== ...
- [Typescript] Improve Readability with TypeScript Numeric Separators when working with Large Numbers
When looking at large numbers in code (such as 1800000) it’s oftentimes difficult for the human eye ...
- [转]概率基础和R语言
概率基础和R语言 R的极客理想系列文章,涵盖了R的思想,使用,工具,创新等的一系列要点,以我个人的学习和体验去诠释R的强大. R语言作为统计学一门语言,一直在小众领域闪耀着光芒.直到大数据的爆发,R语 ...
- Generative Learning algorithms
"generative algorithm models how the data was generated in order to categorize a signal. It ask ...
- Ⅳ Monte Carlo Methods
Dictum: Nutrition books in the world. There is no book in life, there is no sunlight; wisdom withou ...
随机推荐
- 基于netty手写RPC框架
代码目录结构 rpc-common存放公共类 rpc-interface为rpc调用方需要调用的接口 rpc-register提供服务的注册与发现 rpc-client为rpc调用方底层实现 rpc- ...
- 运行带有Activiti modeler时，出现这样的报错： java.rmi.AccessException: Cannot modify this registry
最近在做整合Activiti Modeler工作流在线设计器的工作,运行IDEA时,出现了这样一个错误信息: 原因及解决办法: Activiti默认打开了jmx功能,默认端口为1099,idea中 ...
- 用Python程序温度转换实例
实例:温度转换 (1)分析问题:利用程序进行温度转换,由用户输入温度值,程序给出输出结果:通过语音识别,图像识别等方法自动监听并获得温度信息发布渠道(如收音机.电视机)给出的温度播报源数据,再由程序装 ...
- 轨迹条（Trackbar）
1.创建 createTrackbar(轨迹条名称,窗口名称,滑动条的初始位置,滑动条的最大值,回调函数XXX,不懂) 其中回调函数为 void XXX(滑动条的位置,用户数据)在c++中函数名为指向 ...
- JqGrid参考实例
<div class="gridtable mt5"> <table id="tbList"></table> <di ...
- （原创）MODBUS-TCP协议分析
- prometheus搜索指标显示No datapoints found.
在指标能够在下拉框可以选择到的情况下,还有No datapoints found. 则考虑是时区的问题,详见官方issue https://github.com/prometheus/promethe ...
- JavaScript---Dom树详解,节点查找方式(直接(id,class,tag),间接(父子,兄弟)),节点操作(增删改查,赋值节点,替换节点,),节点属性操作(增删改查),节点文本的操作(增删改查),事件
JavaScript---Dom树详解,节点查找方式(直接(id,class,tag),间接(父子,兄弟)),节点操作(增删改查,赋值节点,替换节点,),节点属性操作(增删改查),节点文本的操作(增删 ...
- mysql 获取指定日期到指定日期 区间段的日期
第一种方法: cross join (就相当于mysql中的循环) CROSS JOIN 把两张表中的数据进行 N * M的组合,即笛卡尔积 这里的两张表利用 union all都有5条数据,所以进行 ...
- CSRF攻击与防御（转）
CSRF概念:CSRF跨站点请求伪造(Cross—Site Request Forgery),跟XSS攻击一样,存在巨大的危害性,你可以这样来理解: 攻击者盗用了你的身份,以你的名义发送 ...