[算法模板]SOS DP

[算法模板]SOS DP

正文

SOS-DP（\(\text{Sum over Subsets}\)）是用来解决这样的问题的：

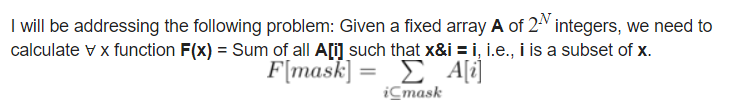
其实就是子集和DP。上面每个\(F[mask]\)里面包含了\(mask\)所有二进制子集的信息。这是一种\(n\log_2 n\)的DP方法。

我们定义一个DP状态\(S(mask,i)\)代表\(mask\)子集中只有最靠右的\(i\)位与其不同的状态。

具体是这样的：

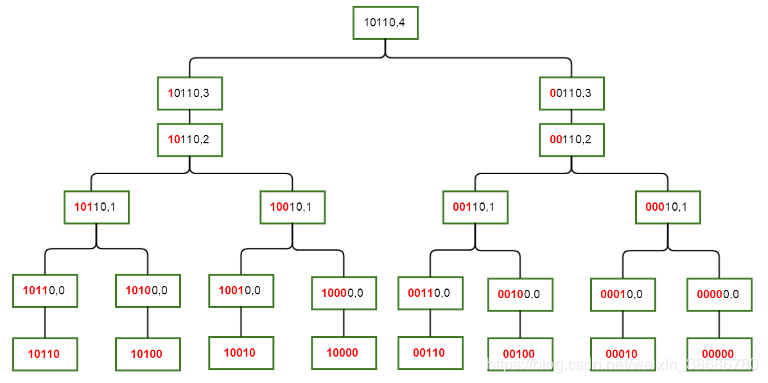
图中描述了\(S(10110,4)\)这个状态和其所有儿子之间的关系。

形象一些解释就是每次我们求解一个状态时，我们只从他的所有子集里和他只差一位的状态转移过来。（众所周知，如果\(A\subseteq B,B\subseteq C\)那么\(A\subseteq\) C）。

放一段代码：

for(int i = 0; i<(1<<N); ++i)
	F[i] = A[i];
for(int i = 0;i < N; ++i) for(int mask = 0; mask < (1<<N); ++mask){
	if(mask & (1<<i))
		F[mask] += F[mask^(1<<i)];
}

所以显然，复杂度\(N\space 2^N\)。如果令值域为\(M\)，那么复杂度就是\(M\log_2M\)。

例题

CF1208F Bits And Pieces

CF165E Compatible Numbers

CF383E Vowels

参考资料

SOS Dynamic Programming [Tutorial]

SOS DP