luogu P3393 逃离僵尸岛-搜索剪枝+spfa

P3393 逃离僵尸岛

题目描述

小a住的国家被僵尸侵略了！小a打算逃离到该国唯一的国际空港逃出这个国家。

该国有N个城市，城市之间有道路相连。一共有M条双向道路。保证没有自环和重边。

K个城市已经被僵尸控制了，如果贸然闯入就会被感染TAT...所以不能进入。由其中任意城市经过不超过S条道路就可以到达的别的城市，就是危险城市。换句话说只要某个没有被占城市到某个被占城市不超过s距离，就是危险。

小a住在1号城市，国际空港在N号城市，这两座城市没有被侵略。小a走每一段道路（从一个城市直接到达另外一个城市）得花一整个白天，所以晚上要住旅店。安全的的城市旅馆比较便宜要P元，而被危险的城市，旅馆要进行安保措施，所以会变贵，为Q元。所有危险的城市的住宿价格一样，安全的城市也是。在1号城市和N城市，不需要住店。

小a比较抠门，所以他希望知道从1号城市到N号城市所需要的最小花费。

输入数据保证存在路径，可以成功逃离。输入数据保证他可以逃离成功。

输入输出格式

输入格式：

第一行4个整数(N,M,K,S)

第二行2个整数(P,Q)

接下来K行，ci，表示僵尸侵占的城市

接下来M行，ai,bi，表示一条无向边

输出格式：

一个整数表示最低花费

输入输出样例

输入样例#1：

13 21 1 1
1000 6000
7
1 2
3 7
2 4
5 8
8 9
2 5
3 4
4 7
9 10
10 11
5 9
7 12
3 6
4 5
1 3
11 12
6 7
8 11
6 13
7 8
12 13

输出样例#1：

11000

说明

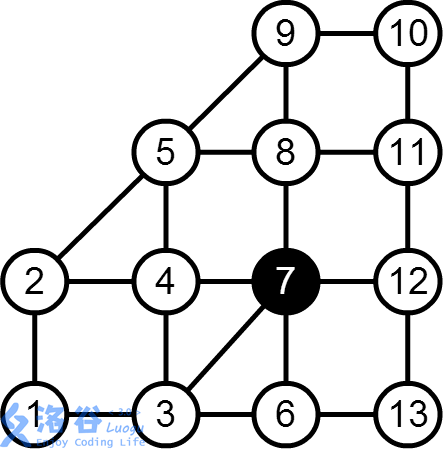
对于20%数据，N<=50

对于100%数据，2 ≦ N ≦ 100000, 1 ≦ M ≦ 200000, 0 ≦ K ≦ N - 2, 0 ≦ S ≦ 100000

1 ≦ P ＜ Q ≦ 100000

注意事项：

①一号点不住店不花费，这点不用说也知道，但是要注意n号点也没有花费。

②题目中有句话说：被僵尸控制的城市不能走，注意分别 控制城市 和 危险城市。

③数组类型开long long，记录最短路的数组赋值一定要大。

④luogu评测毒瘤不开优化AC，开优化TLE。

代码得分分析：

　　先讲A个4点 ：

　　为什么先说60呢？继续听下去。

　　输入的时候记录输入的每条边，并且建边(边权为1)，spfa跑 k 遍，每次记录查询距离<=s的点记录下来，标记为危险城市，然后利用刚开始的记录边状态的数组重新建边，并已花费为边权。

　　最后再次跑一遍spfa输出到n的最短距离就好啦。

贴下代码：

#include<iostream>
#include<cmath>
#include<cstdio>
#include<algorithm>
#include<vector>
#include<cstring>
#include<queue>

#define N 200009
using namespace std;

void in(int &x){
    x=;register char c=getchar();int f=;
    while(!isdigit(c)){if(c=='-')f=-;c=getchar();}
    while(isdigit(c)){x=x*+c-'';c=getchar();}
    x*=f;
}

int n,m,k,S,p,q,head[N],tot,isp[N],d[N];
bool vis[N];
struct node{
    int to,next;
}e[N*];
void add(int u,int v){
    e[++tot].to=v;e[tot].next=head[u];head[u]=tot;
}
queue<int>Q;
void spfa(int s){
    Q.push(s);
    memset(d,0x3f,sizeof(d));memset(vis,,sizeof(vis));d[s]=;vis[s]=;
    while(!Q.empty()){
        int u=Q.front();Q.pop();vis[u]=;
        for(int i=head[u],v;v=e[i].to,i;i=e[i].next){
            if(d[v]>d[u]+){
                d[v]=d[u]+;
                if(!vis[v]){
                    Q.push(v);vis[v]=;
                }
            }
        }
    }for(int i=;i<=n;i++){
        if(d[i]<=S&&isp[i]!=&&i!=s) isp[i]=;
    }
}

void SPFA(int s){
    Q.push(s);
    memset(d,0x3f,sizeof(d));memset(vis,,sizeof(vis));
    d[s]=;vis[s]=;
    while(!Q.empty()){
        int u=Q.front();Q.pop();vis[u]=;
        for(int i=head[u],v;v=e[i].to,i;i=e[i].next){
            int mon=isp[v]==?q:p;
            if(v==n) mon=;
            if(d[v]>d[u]+mon&&isp[v]!=){
                d[v]=d[u]+mon;
                if(!vis[v]){
                    Q.push(v);vis[v]=;
                }
            }
        }
    }
}

int main()
{
    in(n);in(m);in(k);in(S);in(p);in(q);
    for(int i=;i<=k;i++){
        int w;in(w);isp[w]=;
    }for(int i=;i<=m;i++){
        int u,v;in(u);in(v);
        add(u,v);add(v,u);
    }for(int i=;i<=n;i++){
        if(isp[i]==) spfa(i);
    }SPFA();
    printf("%d\n",d[n]);
    return ;
}

这么丑一定不是我写的

　　

　　优化：

　　我们可以很明显的感觉到k遍spfa中有好多没有用的点(已标记)，浪费大量的时间，因此我们可以用 搜索+剪枝 代替k遍spfa处理城市状态。

　　下面可能回跳跃比较大，尽量讲明白。

　　这里用dfs进行搜索，搜索时记录两个变量(u,tot), u表示现在搜到的第u个点，tot表示这个点还可以再去感染几个点。

　　　状态转移：

　　　　  僵尸控制的城市我们称之为感染源。

　　　　　如果这个点不是感染源那么，这个转移向点所连边的点v，dfs(v，tot-1)，v只能继续感染 tot-1个点。

　　　　　如果这个点是感染源，那么这个点便可继续感染 s 个城市，那么转移为dfs( v , s )。

　　　　　如果tot为0以后，则表示已不能再扩展，则return；

　　　进一步优化：

　　　　　也可以说是加了一点小的记忆化吧。

　　　　　用一个dis[ u ]数组表示搜到的 u 个点还可以再感染几个点，如果上一步转移而来的 tot 比目前点的dis[ ]小那么直接return，因为可以扩展的点已经扩展完了。

　　　dfs部分代码：

int dis[];
void dfs(int u,int tot)
{
    f[u]=;
    if(tot<=dis[u])return ;
    dis[u]=tot;
    if(tot==)return ;
    for(int i=head[u];i;i=edge[i].nxt)
    {
        int v=edge[i].to;
        if(start[v]) dfs(v,s);
        else dfs(v,tot-);
    }
}

完整AC代码：

　　别开优化哦！！！

/*....................
作者：Manjusaka
时间：2018/7/5
题目：luogu P3393 逃离僵尸岛
......................*/

#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <queue>
#include <cmath>
using namespace std;
long long n,m,k,s,P,Q;
bool start[];
bool f[];
int p[];
int head[],tot;
struct ahah{
    int nxt,to;
    long long cost;
}edge[];
void add(int x,int y,long long z)
{
    edge[++tot].nxt=head[x];edge[tot].to=y;edge[tot].cost=z; head[x]=tot;
}
long long d[];
queue <int> que;
bool vis[];
void SPFA(int u)
{
    for(int i=;i<=n;i++)d[i]=;
    d[u]=;vis[u]=;que.push(u);
     while(!que.empty())
     {
         int temp=que.front();
         que.pop(); vis[temp]=;
         for(int i=head[temp];i;i=edge[i].nxt)
         {
             int v=edge[i].to;
             if(!start[v]&&d[v]>d[temp]+edge[i].cost)
             {
                 d[v]=d[temp]+edge[i].cost;
                 if(!vis[v])
                 {
                     vis[v]=;
                     que.push(v);
                 }
            }
        }
     }
}
int dis[];
void dfs(int u,int tot)
{
    f[u]=;
    if(tot<=dis[u])return ;
    dis[u]=tot;
    if(tot==)return ;
    for(int i=head[u];i;i=edge[i].nxt)
    {
        int v=edge[i].to;
        if(start[v]) dfs(v,s);
        else dfs(v,tot-);
    }
}
int main()
{
    int x[],y[];
    scanf("%lld%lld%lld%lld%lld%lld",&n,&m,&k,&s,&P,&Q);
    for(int i=;i<=k;i++)scanf("%d",&p[i]),start[p[i]]=;
    for(int i=;i<=m;i++)scanf("%d%d",&x[i],&y[i]),add(x[i],y[i],),add(y[i],x[i],);
    for(int i=;i<=k;i++)
        if(!f[p[i]])dfs(p[i],s);
    tot=;
    for(int i=;i<=m;i++)
    {
        if(y[i]==n)edge[++tot].cost=;
        else if(f[y[i]])edge[++tot].cost=Q;
        else edge[++tot].cost=P;

        if(x[i]==n)edge[++tot].cost=;
        else if(f[x[i]])edge[++tot].cost=Q;
        else edge[++tot].cost=P;
    }
    SPFA();
    printf("%lld",d[n]);
}