HDU - 5894 Pocky(概率)

HDU5894—Pocky

Problem Description：

Let’s talking about something of eating a pocky. Here is a Decorer Pocky, with colorful decorative stripes in the coating, of length L. 
While the length of remaining pocky is longer than d, we perform the following procedure. We break the pocky at any point on it in an equal possibility and this will divide the remaining pocky into two parts. Take the left part and eat it. When it is not longer than d, we do not repeat this procedure. 
Now we want to know the expected number of times we should repeat the procedure above. Round it to 6 decimal places behind the decimal point.

Input：

The first line of input contains an integer N which is the number of test cases. Each of the N lines contains two float-numbers L and d respectively with at most 5 decimal places behind the decimal point where 1 ≤ d, L ≤ 150. 
Output：

For each test case, output the expected number of times rounded to 6 decimal places behind the decimal point in a line.

Sample Input

6
1.0 1.0
2.0 1.0
4.0 1.0
8.0 1.0
16.0 1.0
7.00 3.00

Sample Output

0.000000
1.693147
2.386294
3.079442
3.772589
1.847298

题意：有一个木棒，如果它的长度L大于d就随机从其中一个点处剪成两端，左边的丢掉，右边的留下。继续上述过程，求最终剪木棒次数的期望值。
思路：

1. 队友在最终推公式无果后转战找规律，最后还是是给找出来了，找规律的过程是ln2 = 0.693147。相继尝试多次比例关系后，发现ln(L/d)正好是答案-1，于是就有答案了，提交后AC。赛后搜了一下博客，发现还有积分形式的解法。
2. 首先得知道在x长的木棒上随机选一点的几率为1/x。设在x长的木棒上能剪得次数的函数为f(x)。则有方程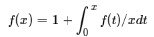然后解方程就可以得到最终的结果为然后敲代码就可以了。

PS：感谢：解惑博客（博主真的很强啊）

代码：

 #include <bits/stdc++.h>
 using namespace std;
 const int maxn = 1e5;
 typedef long long ll;
 int main()
 {
     double l,d;
     int n;
     scanf("%d",&n);
     for(int i = ; i<n; i++)
     {
         scanf("%lf%lf",&l,&d);
         if(l<=d)
             printf("%.6f\n",0.0);
         else
             printf("%.6f\n",log(l/d)+);
     }
     return ;
 }