【ZJOI2017 Round1练习】D2T1 river（二分图）

题意：

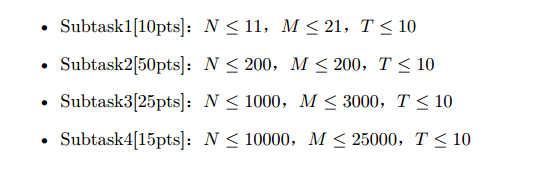
思路：这道题并没有官方题解

没有羊驼在所有三元组中出现就是NO

现在考虑不少于1只的情况

删去其中一只，我们得到了两组点和一些边

我们只要判断这是否为一张二分图，使用暴力染色的方法就有60分了

 #include<cstdio>
 #include<algorithm>
 #define N 10010
 #define M 50010
 using namespace std;
 int T,n,m,edgenum,u,v,ok,isok,root;
 int f[N],vet[M],next[M],head[N],a[M],b[M],c[M],vis[N],flag[N],col[N];
 void add(int u,int v)
 {
     vet[++edgenum]=v;
     next[edgenum]=head[u];
     head[u]=edgenum;
 }
 void dfs(int u)
 {
     vis[u]=;
     for (int e=head[u];e;e=next[e])
     {
         int v=vet[e];
         if (flag[v]) continue;
         if (vis[v])
         {
             if (col[v]==col[u]) ok=;
         }else
         {
             col[v]=col[u]^;
             dfs(v);
         }
     }
 }
 int main()
 {
     freopen("river.in","r",stdin);
     freopen("river.out","w",stdout);
     scanf("%d",&T);
     while (T--)
     {
         scanf("%d%d",&n,&m);
         for (int i=;i<=n;i++) f[i]=;
         for (int i=;i<=m;i++)
         {
             scanf("%d%d%d",&a[i],&b[i],&c[i]);
             f[a[i]]++;f[b[i]]++;f[c[i]]++;
         }
         root=-;
         for (int i=;i<=n;i++) if (f[i]==m) root=i;
         if (root==-){puts("no");continue;}
         edgenum=;
         for (int i=;i<=n;i++) head[i]=;
         for (int i=;i<=m;i++)
         {
             if (a[i]==root){u=b[i];v=c[i];}
             if (b[i]==root){u=a[i];v=c[i];}
             if (c[i]==root){u=a[i];v=b[i];}
             //ed[i].x=u;ed[i].y=v;
             add(u,v);add(v,u);
         }
         isok=;
         //printf("%d\n",root);
         for (int i=;i<=n;i++) if (i!=root)
         {
             if (isok) break;
             for (int j=i+;j<=n;j++) if (j!=root)
             {
                 //printf("%d %d\n",i,j);
                 for (int k=;k<=n;k++) vis[k]=col[k]=;
                 flag[i]=flag[j]=;
                 ok=;
                 for (int k=;k<=n;k++) if (!vis[k]&&k!=i&&k!=j&&k!=root)
                     dfs(k);
                 if (ok) isok=;
                 flag[i]=flag[j]=;
                 if (isok) break;
             }
         }
         if (isok) puts("yes");else puts("no");
     }
 }

至于标程……谁看得懂呢……貌似是暴力加了点优化……

 #include<bits/stdc++.h>
 #define FT first
 #define SC second
 #define PB push_back
 #define MP make_pair
 #define REP(i, l, r) for(int i = (l); i <= (r); i++)
 #define PER(i, r, l) for(int i = (r); i >= (l); i--)
 #define FOR(i, n) for(int i = 0; i < (n); i++)
 #define ROF(i, n) for(int i = (n) - 1; i >= 0; i--)
 #define VEP(i, x) for(int i = 0; i < x.size(); i++)
 #define DFOR(i, x, y) for(int i = hd[x], y = e[i].to; i; i = e[i].nxt, y = e[i].to)
 #define MEM(a, b) memset(a, b, sizeof(a))
 #define rint read<int>()
 #define rll read<LL>()
 
 using namespace std;
 typedef long long LL;
 typedef long double LD;
 typedef pair<int, int> PI;
 const int inf = 0x7fffffff;
 const int MOD = ;
 
 template <typename tn>
 inline tn read(){
     char ch; tn f = ;
     while (!isdigit(ch = getchar())) if (ch == '-') f = -;
     tn x = ch - '';
     while (isdigit(ch = getchar())) x = x *  + ch - '';
     return x * f;
 }
 template <typename tn> inline void cmax(tn &a, tn b){ if (a < b) a = b; }
 template <typename tn> inline void cmin(tn &a, tn b){ if (a > b) a = b; }
 
 const int N =  + ;
 struct Edge{ int nxt, to; } e[N * ];
 struct Data{ int f, safe, danger; };
 int color[N], x[N], y[N], z[N], sz[N], rt, tail, hd[N], tot, dep[N], S, T;
 void add(int x, int y){ e[++tail] = (Edge){hd[x], y}, hd[x] = tail; }
 Data dfs(int x, int c, int f){
     color[x] = c;
     Data cur;
     cur.safe = inf, cur.danger = -, cur.f = ;
     DFOR(i, x, y) if (y != f && color[y] != -)
         if (!~color[y]){
             dep[y] = dep[x] + ;
             Data now = dfs(y, c ^ , x);
             cur.f += now.f;    if (cur.f > ) { return cur;}
             cmin(cur.safe, now.safe), cmax(cur.danger, now.danger);
         } else if (dep[y] < dep[x]) if (color[x] ^ color[y]) cmin(cur.safe, dep[y]); else{
             cmax(cur.danger, dep[y]);
             if (!S) S = x, T = y;
             if (S != x && S != y) S = -;
             if (T != x && T != y) T = -;
         }
     if (cur.safe <= dep[x] && cur.danger >= dep[x]) cur.f = ;
     else if (cur.danger >= dep[x]) cur.f++, cur.danger = -;
     return cur;
 }
 int main(){
     freopen("river.in", "r", stdin);
     freopen("river.out", "w", stdout);
     int Cas = rint;
     while (Cas--){
         int n = rint, m = rint;
         MEM(sz, ), MEM(hd, ), tail = , rt = ;
         REP(i, , m) sz[x[i] = rint]++, sz[y[i] = rint]++, sz[z[i] = rint]++;
         REP(i, , n) if (sz[i] == m) rt = i;
         if (rt){
             bool ans = ;
             REP(i, , m){
                 if (x[i] == rt) swap(x[i], z[i]);
                 if (y[i] == rt) swap(y[i], z[i]);
                 add(x[i], y[i]), add(y[i], x[i]);
             }
             REP(i, , n) if (i != rt) {
                 MEM(color, -), color[i] = -;
                 int flag = , tot = ;
                 REP(i, , n) if (color[i] == -){
                     S = , T = ;
                     int tmp = dfs(i, , ).f;
                     if (S >  || T > ) cmin(tmp, );
                     tot += tmp;
                     if (tot > ) {flag = ; break;}
                 }
                 if (flag) {ans = ; break;}
             }
             if (ans) printf("yes\n"); else printf("no\n");
         } else printf("no\n");
     }
 }