python-hanoi

 #!/usr/bin/env python
 #-*- coding:utf-8 -*-
 ############################
 #File Name: hanoi.py
 #Author: frank
 #Mail: frank0903@aliyun.com
 #Created Time:2018-04-30 09:36:13
 ############################

 #基本思想是:先将最大的圆盘从src搬到dst
 #如果n=1，那么直接将圆盘从src搬到dst;
 #如果n=2，那么先将第1个圆盘从src搬到mid上,然后将第2个圆盘从src搬到dst,然后将第1个圆盘从mid搬到dst上;
 #如果有n个圆盘,那么先将n-1个圆盘从src搬到mid上,然后将第n个圆盘从srt搬到dst, 然后将n-1个圆盘从mid搬到dst;以此类推
 #可以这么理解,将n个圆盘抽象成"2个"圆盘,第n个圆盘当做"第2个"圆盘,另外的n-1个圆盘抽象成"第1个"圆盘,那么就可以当做是"2个"圆盘的搬运;
 #不同层次的圆盘移动时，src,mid,dst会发生相应的变化,而不是最初第n个圆盘移动时的位置,这样就保证所有移动的准确性且不会冲突
 #总之,抽象成"2个圆盘"的思路,并保证圆盘移动步骤的闭合性,就能确保程序的正确运行
 count = 0

 def hanoi(n, src, mid, dst):
     global count

     if n == 1:
     ¦   print("{}:{}--->{}".format(n, src, dst))
     ¦   count += 1
     else:
     ¦   hanoi(n-1, src, dst, mid)
     ¦   print("{}:{}--->{}".format(n, src, dst))
     ¦   hanoi(n-1, mid, src, dst)
     ¦   count += 1

 hanoi(3, "A", "B", "C")
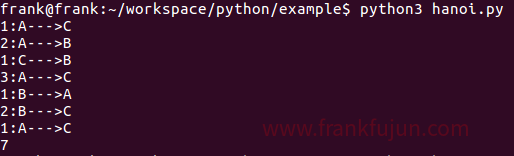
 print(count)

 #n=3时,圆盘搬运的具体过程如下:
 #
 #hanoi(2, A, C, B)
 #    hanoi(1, A, B, C)
 #        print("{}:{}--->{}".format(1, A, C)) ==={1:A--->C}
 #    print("{}:{}--->{}".format(2, A, B)) ==={2:A--->B}
 #    hanoi(1, C, A, B)
 #        print("{}:{}--->{}".format(1, C, B)) ==={1:C--->B}
 #print("{}:{}--->{}".format(3, A, C)) ==={3:A--->C}
 #hanoi(2, B, A, C)
 #    hanoi(1, B, C, A)
 #        print("{}:{}--->{}".format(1, B, A)) ==={1:B--->A}
 #    print("{}:{}--->{}".format(2, B, C)) ==={2:B--->C}
 #    hanoi(1, A, B, C)
 #        print("{}:{}--->{}".format(1, A, C)) ==={1:A--->C}