[NOIP2010] 提高组 洛谷P1514 引水入城

题目描述

在一个遥远的国度，一侧是风景秀美的湖泊，另一侧则是漫无边际的沙漠。该国的行政区划十分特殊，刚好构成一个N 行M 列的矩形，如上图所示，其中每个格子都代表一座城市，每座城市都有一个海拔高度。

为了使居民们都尽可能饮用到清澈的湖水，现在要在某些城市建造水利设施。水利设施有两种，分别为蓄水厂和输水站。蓄水厂的功能是利用水泵将湖泊中的水抽取到所在城市的蓄水池中。

因此，只有与湖泊毗邻的第1 行的城市可以建造蓄水厂。而输水站的功能则是通过输水管线利用高度落差，将湖水从高处向低处输送。故一座城市能建造输水站的前提，是存在比它海拔更高且拥有公共边的相邻城市，已经建有水利设施。由于第N 行的城市靠近沙漠，是该国的干旱区，所以要求其中的每座城市都建有水利设施。那么，这个要求能否满足呢？如果能，请计算最少建造几个蓄水厂；如果不能，求干旱区中不可能建有水利设施的城市数目。

输入输出格式

输入格式：

输入文件的每行中两个数之间用一个空格隔开。输入的第一行是两个正整数N 和M，表示矩形的规模。接下来N 行，每行M 个正整数，依次代表每座城市的海拔高度。

输出格式：

输出有两行。如果能满足要求，输出的第一行是整数1，第二行是一个整数，代表最少建造几个蓄水厂；如果不能满足要求，输出的第一行是整数0，第二行是一个整数，代表有几座干旱区中的城市不可能建有水利设施。

输入输出样例

输入样例#1：

【输入样例1】
2 5
9 1 5 4 3
8 7 6 1 2

【输入样例2】
3 6
8 4 5 6 4 4
7 3 4 3 3 3
3 2 2 1 1 2

输出样例#1：

【输出样例1】
1
1

【输出样例2】
1
3

说明

【样例1 说明】

只需要在海拔为9 的那座城市中建造蓄水厂，即可满足要求。

【样例2 说明】

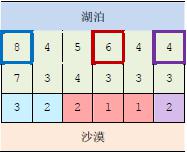
上图中，在3 个粗线框出的城市中建造蓄水厂，可以满足要求。以这3 个蓄水厂为源头

在干旱区中建造的输水站分别用3 种颜色标出。当然，建造方法可能不唯一。

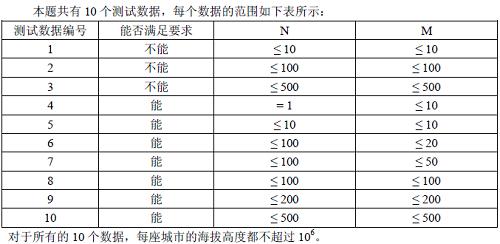
【数据范围】

在每个沿海城市BFS，flood-fill填充干旱区。

将每个城市能支援的地区以线段的形式记录下来（一定是连续的线段，否则若中间空出来一段，问题无解），之后就是最少线段覆盖问题了。

 /*by SilverN*/
 #include<algorithm>
 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<cmath>
 using namespace std;
 const int mxn=;
 const int mx[]={,,,-,};
 const int my[]={,,,,-};
 int read(){
     int x=,f=;char ch=getchar();
     while(ch<'' || ch>''){if(ch=='-')f=-;ch=getchar();}
     while(ch>='' && ch<=''){x=x*+ch-'';ch=getchar();}
     return x*f;
 }
 struct slu{
     int l,r;
 }a[mxn];int cnt=;
 int cmp(const slu a,const slu b){return a.l<b.l;}
 int n,m;
 int mp[mxn][mxn];
 bool vis[mxn][mxn];
 bool ari[mxn];
 int qx[],qy[];
 int hd,tl;
 void BFS(int sy){
 //    memset(qx,0,sizeof qx);
 //    memset(qy,0,sizeof qy);
     memset(vis,,sizeof vis);
     hd=,tl=;
     qx[++hd]=;qy[hd]=sy;
     vis[][sy]=;
     while(hd!=tl+){
         int x=qx[hd],y=qy[hd];hd++;
         for(int i=;i<=;++i){
             int nx=x+mx[i],ny=y+my[i];
             if(nx< || nx>n || ny< || ny>m || vis[nx][ny])continue;
             if(mp[nx][ny]<mp[x][y]){
                 qx[++tl]=nx;qy[tl]=ny;
                 vis[nx][ny]=;
             }
         }
     }
     int last=;
     for(register int i=;i<=m;i++){
         if(vis[n][i]){
             if(!last){a[++cnt].l=i;a[cnt].r=i;last=;}
             else{a[cnt].r=i;}
             ari[i]=;
         }
         else if(last)a[cnt].r=i-,last=;
     }
     return;
 }
 int ans=;
 void clc(){
     int R=,mx=;
     int i=;
     while(i<=cnt){
         mx=;
         while(a[i].l<=R+ && i<=cnt){
             mx=max(mx,a[i].r);
             ++i;
         }
         ans++;
         R=mx;
         if(R==m)break;
     }
     return;
 }
 int main(){
     n=read();m=read();
     int i,j;
     for(register int i=;i<=n;i++)
         for(register int j=;j<=m;j++)
             mp[i][j]=read();
     for(i=;i<=m;i++) if(!vis[][i]) BFS(i);
     int cct=;
     for(i=;i<=m;i++)if(ari[i])cct++;
     if(cct!=m){
         printf("0\n%d\n",m-cct);
         return ;
     }
     sort(a+,a+cnt+,cmp);
     clc();
     printf("1\n%d\n",ans);
     return ;
 }

，