【模板】prufer序列

如何构造一个prufer序列？

我们给一棵无根树的节点编上号，每次找到一个编号最小的度为1节点，删除它，并输出与它连接的点的编号，直到只剩下两个节点。

这样，我们就构造出来了一个prufer序列。

通过prufer序列的构造方式我们可以知道：

性质1：一棵节点数为n的树的prufer序列的长度为n-2。

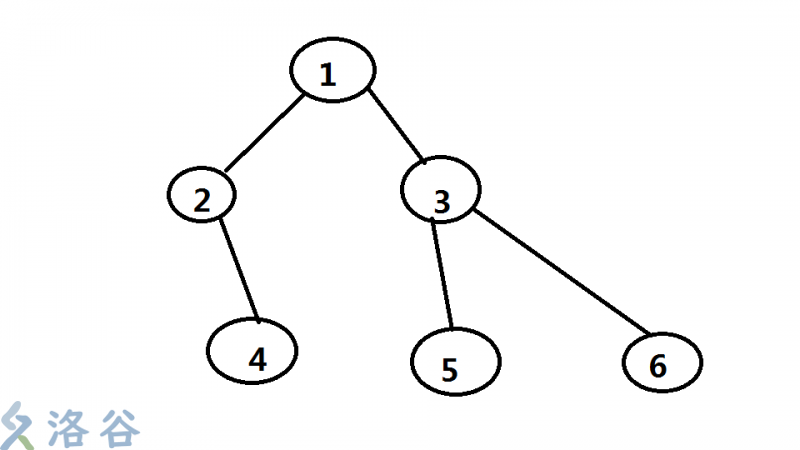
比如，这棵树的prufer序列是2,1,3,3

从这个样例我们也可以知道：

性质2：每一个编号在prufer序列中出现的次数是它在树中的度数\(-1\)。

由prufer序列转化为无根树。

取出prufer最前面的点\(u\)。

每次从点集中找到最小的没有在树中的点\(v\)，连接\(u\),\(v\)。

当点集中只剩2点时，连接这两个点。