机器学习经典算法之PageRank

Google 的两位创始人都是斯坦福大学的博士生，他们提出的 PageRank 算法受到了论文影响力因子的评价启发。当一篇论文被引用的次数越多，证明这篇论文的影响力越大。正是这个想法解决了当时网页检索质量不高的问题。

/*请尊重作者劳动成果，转载请标明原文链接：*/

/* https://www.cnblogs.com/jpcflyer/p/11180263.html * /

一、 PageRank 的简化模型

我们先来看下 PageRank 是如何计算的。

我假设一共有 4 个网页 A、B、C、D。它们之间的链接信息如图所示：

这里有两个概念你需要了解一下。

出链指的是链接出去的链接。入链指的是链接进来的链接。比如图中 A 有 2 个入链，3 个出链。

简单来说，一个网页的影响力 = 所有入链集合的页面的加权影响力之和，用公式表示为：

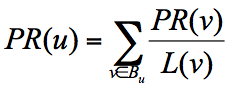
u 为待评估的页面， B_{u} 为页面 u 的入链集合。针对入链集合中的任意页面 v，它能给 u 带来的影响力是其自身的影响力 PR(v) 除以 v 页面的出链数量，即页面 v 把影响力 PR(v) 平均分配给了它的出链，这样统计所有能给 u 带来链接的页面 v，得到的总和就是网页 u 的影响力，即为 PR(u)。

所以你能看到，出链会给被链接的页面赋予影响力，当我们统计了一个网页链出去的数量，也就是统计了这个网页的跳转概率。

在这个例子中，你能看到 A 有三个出链分别链接到了 B、C、D 上。那么当用户访问 A 的时候，就有跳转到 B、C 或者 D 的可能性，跳转概率均为 1/3。

B 有两个出链，链接到了 A 和 D 上，跳转概率为 1/2。

这样，我们可以得到 A、B、C、D 这四个网页的转移矩阵 M：

我们假设 A、B、C、D 四个页面的初始影响力都是相同的，即：

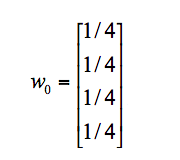
当进行第一次转移之后，各页面的影响力 w_{1} 变为：

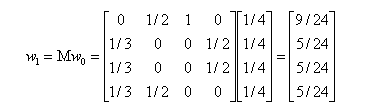
然后我们再用转移矩阵乘以 w_{1} 得到 w_{2} 结果，直到第 n 次迭代后 w_{n} 影响力不再发生变化，可以收敛到 (0.3333，0.2222，0.2222，0.2222），也就是对应着 A、B、C、D 四个页面最终平衡状态下的影响力。

你能看出 A 页面相比于其他页面来说权重更大，也就是 PR 值更高。而 B、C、D 页面的 PR 值相等。

至此，我们模拟了一个简化的 PageRank 的计算过程，实际情况会比这个复杂，可能会面临两个问题：

1. 等级泄露（Rank Leak）：如果一个网页没有出链，就像是一个黑洞一样，吸收了其他网页的影响力而不释放，最终会导致其他网页的 PR 值为 0。

2. 等级沉没（Rank Sink）：如果一个网页只有出链，没有入链（如下图所示），计算的过程迭代下来，会导致这个网页的 PR 值为 0（也就是不存在公式中的 V）。

针对等级泄露和等级沉没的情况，我们需要灵活处理。

比如针对等级泄露的情况，我们可以把没有出链的节点，先从图中去掉，等计算完所有节点的 PR 值之后，再加上该节点进行计算。不过这种方法会导致新的等级泄露的节点的产生，所以工作量还是很大的。

有没有一种方法，可以同时解决等级泄露和等级沉没这两个问题呢？

二、 PageRank 的随机浏览模型

为了解决简化模型中存在的等级泄露和等级沉没的问题，拉里·佩奇提出了 PageRank 的随机浏览模型。他假设了这样一个场景：用户并不都是按照跳转链接的方式来上网，还有一种可能是不论当前处于哪个页面，都有概率访问到其他任意的页面，比如说用户就是要直接输入网址访问其他页面，虽然这个概率比较小。

所以他定义了阻尼因子 d，这个因子代表了用户按照跳转链接来上网的概率，通常可以取一个固定值 0.85，而 1-d=0.15 则代表了用户不是通过跳转链接的方式来访问网页的，比如直接输入网址。

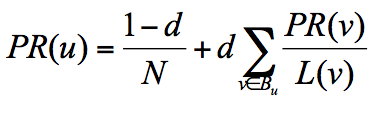
其中 N 为网页总数，这样我们又可以重新迭代网页的权重计算了，因为加入了阻尼因子 d，一定程度上解决了等级泄露和等级沉没的问题。

通过数学定理（这里不进行讲解）也可以证明，最终 PageRank 随机浏览模型是可以收敛的，也就是可以得到一个稳定正常的 PR 值。

三、 PageRank 在社交影响力评估中的应用

网页之间会形成一个网络，是我们的互联网，论文之间也存在着相互引用的关系，可以说我们所处的环境就是各种网络的集合。

只要是有网络的地方，就存在出链和入链，就会有 PR 权重的计算，也就可以运用我们今天讲的 PageRank 算法。

我们可以把 PageRank 算法延展到社交网络领域中。比如在微博上，如果我们想要计算某个人的影响力，该怎么做呢？

一个人的微博粉丝数并不一定等于他的实际影响力。如果按照 PageRank 算法，还需要看这些粉丝的质量如何。如果有很多明星或者大 V 关注，那么这个人的影响力一定很高。如果粉丝是通过购买僵尸粉得来的，那么即使粉丝数再多，影响力也不高。

同样，在工作场景中，比如说脉脉这个社交软件，它计算的就是个人在职场的影响力。如果你的工作关系是李开复、江南春这样的名人，那么你的职场影响力一定会很高。反之，如果你是个学生，在职场上被链入的关系比较少的话，职场影响力就会比较低。

同样，如果你想要看一个公司的经营能力，也可以看这家公司都和哪些公司有合作。如果它合作的都是世界 500 强企业，那么这个公司在行业内一定是领导者，如果这个公司的客户都是小客户，即使数量比较多，业内影响力也不一定大。

除非像淘宝一样，有海量的中小客户，最后大客户也会找上门来寻求合作。所以权重高的节点，往往会有一些权重同样很高的节点在进行合作。

四、 如何使用工具实现 PageRank 算法

PageRank 算法工具在 sklearn 中并不存在，我们需要找到新的工具包。实际上有一个关于图论和网络建模的工具叫 NetworkX，它是用 Python 语言开发的工具，内置了常用的图与网络分析算法，可以方便我们进行网络数据分析。

上节课，我举了一个网页权重的例子，假设一共有 4 个网页 A、B、C、D，它们之间的链接信息如图所示：

针对这个例子，我们看下用 NetworkX 如何计算 A、B、C、D 四个网页的 PR 值，具体代码如下：

 import networkx as nx

 # 创建有向图

 G = nx.DiGraph()

 # 有向图之间边的关系

 edges = [("A", "B"), ("A", "C"), ("A", "D"), ("B", "A"), ("B", "D"), ("C", "A"), ("D", "B"), ("D", "C")]

 for edge in edges:

     G.add_edge(edge[0], edge[1])

 pagerank_list = nx.pagerank(G, alpha=1)

 print("pagerank 值是：", pagerank_list)

NetworkX 工具把中间的计算细节都已经封装起来了，我们直接调用 PageRank 函数就可以得到结果：

 pagerank 值是： {'A': 0.33333396911621094, 'B': 0.22222201029459634, 'C': 0.22222201029459634, 'D': 0.22222201029459634}

好了，运行完这个例子之后，我们来看下 NetworkX 工具都有哪些常用的操作。

1. 关于图的创建

图可以分为无向图和有向图，在 NetworkX 中分别采用不同的函数进行创建。无向图指的是不用节点之间的边的方向，使用 nx.Graph() 进行创建；有向图指的是节点之间的边是有方向的，使用 nx.DiGraph() 来创建。在上面这个例子中，存在 A→D 的边，但不存在 D→A 的边。

2.关于节点的增加、删除和查询

如果想在网络中增加节点，可以使用 G.add_node(‘A’) 添加一个节点，也可以使用 G.add_nodes_from([‘B’,‘C’,‘D’,‘E’]) 添加节点集合。如果想要删除节点，可以使用 G.remove_node(node) 删除一个指定的节点，也可以使用 G.remove_nodes_from([‘B’,‘C’,‘D’,‘E’]) 删除集合中的节点。

那么该如何查询节点呢？

如果你想要得到图中所有的节点，就可以使用 G.nodes()，也可以用 G.number_of_nodes() 得到图中节点的个数。

3. 关于边的增加、删除、查询

增加边与添加节点的方式相同，使用 G.add_edge(“A”, “B”) 添加指定的“从 A 到 B”的边，也可以使用 add_edges_from 函数从边集合中添加。我们也可以做一个加权图，也就是说边是带有权重的，使用 add_weighted_edges_from 函数从带有权重的边的集合中添加。在这个函数的参数中接收的是 1 个或多个三元组 [u,v,w] 作为参数，u、v、w 分别代表起点、终点和权重。

另外，我们可以使用 remove_edge 函数和 remove_edges_from 函数删除指定边和从边集合中删除。

另外可以使用 edges() 函数访问图中所有的边，使用 number_of_edges() 函数得到图中边的个数。

以上是关于图的基本操作，如果我们创建了一个图，并且对节点和边进行了设置，就可以找到其中有影响力的节点，原理就是通过 PageRank 算法，使用 nx.pagerank(G) 这个函数，函数中的参数 G 代表创建好的图。

五、 如何用 PageRank 揭秘希拉里邮件中的人物关系

了解了 NetworkX 工具的基础使用之后，我们来看一个实际的案例：希拉里邮件人物关系分析。

希拉里邮件事件相信你也有耳闻，对这个数据的背景我们就不做介绍了。你可以从 GitHub 上下载这个数据集： https://github.com/cystanford/PageRank

整个数据集由三个文件组成：Aliases.csv，Emails.csv 和 Persons.csv，其中 Emails 文件记录了所有公开邮件的内容，发送者和接收者的信息。Persons 这个文件统计了邮件中所有人物的姓名及对应的 ID。因为姓名存在别名的情况，为了将邮件中的人物进行统一，我们还需要用 Aliases 文件来查询别名和人物的对应关系。

整个数据集包括了 9306 封邮件和 513 个人名，数据集还是比较大的。不过这一次我们不需要对邮件的内容进行分析，只需要通过邮件中的发送者和接收者（对应 Emails.csv 文件中的 MetadataFrom 和 MetadataTo 字段）来绘制整个关系网络。因为涉及到的人物很多，因此我们需要通过 PageRank 算法计算每个人物在邮件关系网络中的权重，最后筛选出来最有价值的人物来进行关系网络图的绘制。

了解了数据集和项目背景之后，我们来设计到执行的流程步骤：

首先我们需要加载数据源；

在准备阶段：我们需要对数据进行探索，在数据清洗过程中，因为邮件中存在别名的情况，因此我们需要统一人物名称。另外邮件的正文并不在我们考虑的范围内，只统计邮件中的发送者和接收者，因此我们筛选 MetadataFrom 和 MetadataTo 这两个字段作为特征。同时，发送者和接收者可能存在多次邮件往来，需要设置权重来统计两人邮件往来的次数。次数越多代表这个边（从发送者到接收者的边）的权重越高；

在挖掘阶段：我们主要是对已经设置好的网络图进行 PR 值的计算，但邮件中的人物有 500 多人，有些人的权重可能不高，我们需要筛选 PR 值高的人物，绘制出他们之间的往来关系。在可视化的过程中，我们可以通过节点的 PR 值来绘制节点的大小，PR 值越大，节点的绘制尺寸越大。

设置好流程之后，实现的代码如下：

 # -*- coding: utf-8 -*-

 # 用 PageRank 挖掘希拉里邮件中的重要任务关系

 import pandas as pd

 import networkx as nx

 import numpy as np

 from collections import defaultdict

 import matplotlib.pyplot as plt

 # 数据加载

 emails = pd.read_csv("./input/Emails.csv")

 # 读取别名文件

 file = pd.read_csv("./input/Aliases.csv")

 aliases = {}

 for index, row in file.iterrows():

     aliases[row['Alias']] = row['PersonId']

 # 读取人名文件

 file = pd.read_csv("./input/Persons.csv")

 persons = {}

 for index, row in file.iterrows():

     persons[row['Id']] = row['Name']

 # 针对别名进行转换        

 def unify_name(name):

     # 姓名统一小写

     name = str(name).lower()

     # 去掉, 和 @后面的内容

     name = name.replace(",","").split("@")[0]

     # 别名转换

     if name in aliases.keys():

         return persons[aliases[name]]

     return name

 # 画网络图

 def show_graph(graph, layout='spring_layout'):

     # 使用 Spring Layout 布局，类似中心放射状

     if layout == 'circular_layout':

         positions=nx.circular_layout(graph)

     else:

         positions=nx.spring_layout(graph)

     # 设置网络图中的节点大小，大小与 pagerank 值相关，因为 pagerank 值很小所以需要 *20000

     nodesize = [x['pagerank']*20000 for v,x in graph.nodes(data=True)]

     # 设置网络图中的边长度

     edgesize = [np.sqrt(e[2]['weight']) for e in graph.edges(data=True)]

     # 绘制节点

     nx.draw_networkx_nodes(graph, positions, node_size=nodesize, alpha=0.4)

     # 绘制边

     nx.draw_networkx_edges(graph, positions, edge_size=edgesize, alpha=0.2)

     # 绘制节点的 label

     nx.draw_networkx_labels(graph, positions, font_size=10)

     # 输出希拉里邮件中的所有人物关系图

     plt.show()

 # 将寄件人和收件人的姓名进行规范化

 emails.MetadataFrom = emails.MetadataFrom.apply(unify_name)

 emails.MetadataTo = emails.MetadataTo.apply(unify_name)

 # 设置遍的权重等于发邮件的次数

 edges_weights_temp = defaultdict(list)

 for row in zip(emails.MetadataFrom, emails.MetadataTo, emails.RawText):

     temp = (row[0], row[1])

     if temp not in edges_weights_temp:

         edges_weights_temp[temp] = 1

     else:

         edges_weights_temp[temp] = edges_weights_temp[temp] + 1

 # 转化格式 (from, to), weight => from, to, weight

 edges_weights = [(key[0], key[1], val) for key, val in edges_weights_temp.items()]

 # 创建一个有向图

 graph = nx.DiGraph()

 # 设置有向图中的路径及权重 (from, to, weight)

 graph.add_weighted_edges_from(edges_weights)

 # 计算每个节点（人）的 PR 值，并作为节点的 pagerank 属性

 pagerank = nx.pagerank(graph)

 # 将 pagerank 数值作为节点的属性

 nx.set_node_attributes(graph, name = 'pagerank', values=pagerank)

 # 画网络图

 show_graph(graph)

 # 将完整的图谱进行精简

 # 设置 PR 值的阈值，筛选大于阈值的重要核心节点

 pagerank_threshold = 0.005

 # 复制一份计算好的网络图

 small_graph = graph.copy()

 # 剪掉 PR 值小于 pagerank_threshold 的节点

 for n, p_rank in graph.nodes(data=True):

     if p_rank['pagerank'] < pagerank_threshold:

         small_graph.remove_node(n)

 # 画网络图, 采用 circular_layout 布局让筛选出来的点组成一个圆

 show_graph(small_graph, 'circular_layout')

运行结果如下：

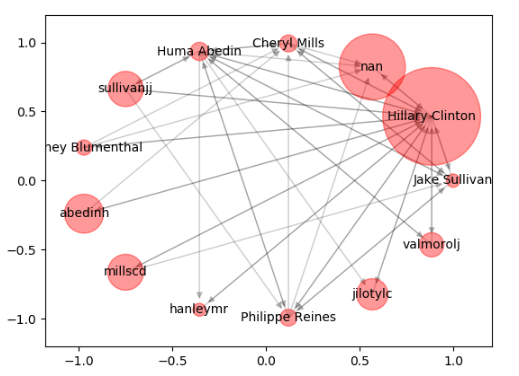
针对代码中的几个模块我做个简单的说明：

1. 函数定义

人物的名称需要统一，因此我设置了 unify_name 函数，同时设置了 show_graph 函数将网络图可视化。NetworkX 提供了多种可视化布局，这里我使用 spring_layout 布局，也就是呈中心放射状。

除了 spring_layout 外，NetworkX 还有另外三种可视化布局，circular_layout（在一个圆环上均匀分布节点），random_layout（随机分布节点 ），shell_layout（节点都在同心圆上）。

2. 计算边权重

邮件的发送者和接收者的邮件往来可能不止一次，我们需要用两者之间邮件往来的次数计算这两者之间边的权重，所以我用 edges_weights_temp 数组存储权重。而上面介绍过在 NetworkX 中添加权重边（即使用 add_weighted_edges_from 函数）的时候，接受的是 u、v、w 的三元数组，因此我们还需要对格式进行转换，具体转换方式见代码。

3.PR 值计算及筛选

我使用 nx.pagerank(graph) 计算了节点的 PR 值。由于节点数量很多，我们设置了 PR 值阈值，即 pagerank_threshold=0.005，然后遍历节点，删除小于 PR 值阈值的节点，形成新的图 small_graph，最后对 small_graph 进行可视化（对应运行结果的第二张图）。

搜索关注微信公众号“程序员姜小白”，获取更新精彩内容哦。