codeforces C. Primes and Multiplication（快速幂 唯一分解定理）

题目链接：http://codeforces.com/contest/1228/problem/C

题解:给定一个函数f,g，题目有描述其中的表达式含义和两者之间的关系。

然后计算：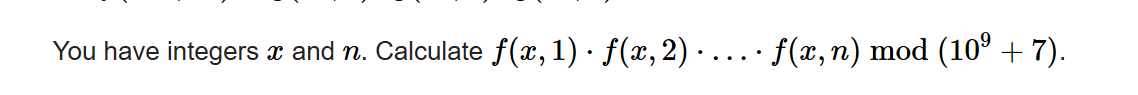

首先把给定的x用唯一分解定理分解出素因子

因为在1-n中，n/p(素因子)的值就是其1-n中有多少个数能整除p，n/p^2就是有多少个数能被p^2整除，所以做一次循环，每次n=n/p，直到n为0，sum记录每次n除以p的个数，就是1-n中能整除p的次方的数的幂指数之和了。

举个例子，45和3，n=45,p=3,第一次循环45/3=15，sum+=15 表示其中1-45中有15个数能整除3，n = 15,p,=3; n/p=5,表示1-45中有5个数能被3^2整除，sum+=5,n = 5,p=3 ； 5/3=1,表示1-45有1个数能整除3^3，sum+=1;

最终sum = 16

AC代码：

#include<iostream>
#include<algorithm>
#include<cstring>
#include<set>
#include<map>
#include<vector>
#define inf 0x3f3f3f3f
using namespace std;
typedef long long ll;
ll mod = 1e9+7;
ll x,n;
ll quick_pow(ll a,ll b){ //调用快速幂算法
	ll res = 1;
	while(b){
		if(b&1) res = res*a%mod;
		a = a*a%mod;
		b>>=1;
	}
	return res;
}
ll cal_g(ll y,ll p){
	ll m = y,sum = 0;
	while(m){
		sum+=m/p;  //计算素因子在1-n的"贡献"
		m/=p;
	}
	return quick_pow(p,sum);
}
int main(){
	ios::sync_with_stdio(false);
	cin>>x>>n;
	ll ans = 1;
	vector<ll> v;
    for(int i=2;i*i<=x;++i){
    	if(x%i==0){                 //唯一分解定理
    		ans = ans * cal_g(n,i)%mod;
			while(x%i==0){
				x/=i;
			}
		}
    }
    if(x!=1) ans = ans*cal_g(n,x)%mod;
	cout<<ans;
	return 0;
}

ac代码：