codeforces 1285E. Delete a Segment

链接:https://codeforces.com/problemset/problem/1285/E

题意：给一个数轴上有n个线段集，线段集若有相交，则合并为一个新的合并线段集，比如[1,6]和[2,9]，因为两个线段有相交，所以要合并为[1,9]，先问删掉给定的n个线段集中的任意一个，剩下的n-1个线段组成的新的合并线段集数量最大是多少？

思路：

这道题首先想到的是并查集做法，枚举删除任意一条线段后，剩下的线段组成的集合是多少，取max，这个复杂度有n² × 并查集复杂度，显然是不行的。那么考虑离散化处理线段左右端点，然后去扫描。

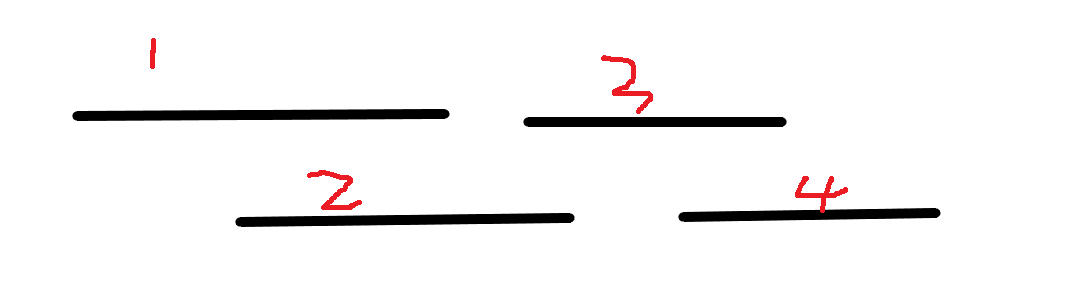
如图所示，线段1，2，3，4离散化处理左右端点，然后排个序并标记一下线段号，开始扫描，扫描到的端点先放入multiset集合中去，最初扫描到线段1的左端点L₁，然后是L₂，再然后是R₁，此时我们发现，线段1已经扫描完比，那么删除这条线段1的左右端点，发现集合中只剩下了L₂，且下一个要扫描到的端点是L₃，此时就意味着删除点线段2后，线段1和线段3是不相交的，那么删除线段2后，新线段合并集合数量就会+1。同理当扫描到R₂时，整个线段2已经扫描完毕，删除集合中线段2左右端点，集合只剩下线段3的左端点，且下一个元素是线段4的左端点，说明线段2和线段4不相交，那么此时删除线段3，就意味着线段2和线段4不相连，新线段合并集合数量就+1，根据以上这个性质，扫描的时候枚举下个元素是左端点还是右端点，记录删除每个线段删除后，合并集合会增加多少，最终拿最初不删除任何线段得到的合并线段集数量+max（删除某一线段增加的数量）就是答案

当然要特判一种情况：

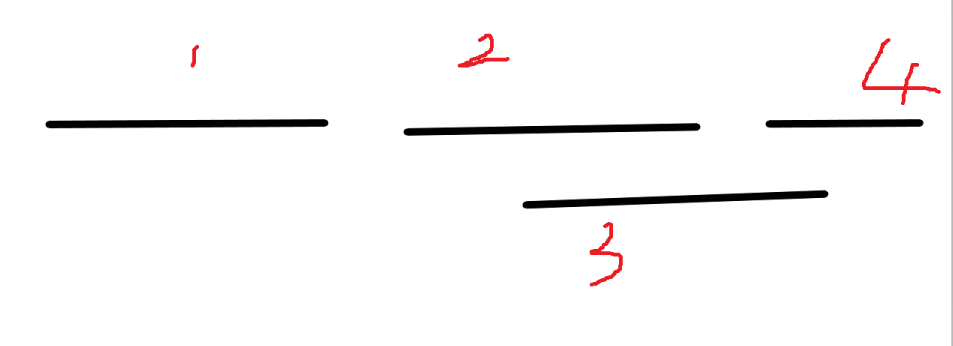
如图所示线段1这种情况，删除这条线段，则新合并集是-1，因为它没有和任何线段有相交，本身就构成一个独立的合并线段集，删除就减少1个合并线段集，特判这种情况即可。

AC代码:

 #include<iostream>
 #include<vector>
 #include<cstdlib>
 #include<cstdio>
 #include<algorithm>
 #include<cmath>
 #include<set>
 #include<cstring>
 #include<queue>
 #include<map>
 using namespace std;
 typedef long long ll;
 const int maxn = 4e5+;
 pair<ll,ll> p[maxn];
 int cnt[maxn];
 int main()
 {
     int t;
     cin>>t;
     while(t--){
         int n;
         cin>>n;
         for(int i = ;i<=n;i++){
             ll l,r;
             cin>>l>>r;
             p[*i-] = make_pair(l,-i);//离散化记录区间左右端点的位置和区间标号i
             p[*i] = make_pair(r,i);
             cnt[i] = ;
         }
         sort(p+,p+*n+);
         int ans = ;
         multiset<int> s;
         for(int i = ;i<=*n;i++){
             if(p[i].second < ){//如果是左端点，就插入set
                 s.insert(-p[i].second );
             }
             else{
                 s.erase(s.find(p[i].second));//如果是右端点，就把这个区间删除
             }
             if(s.size() == ) ans++;//如果集合是空，记录一个合并的区间
             if(s.size() ==  && p[i].second >  && p[i+].second <  && p[i+].first > p[i].first ){
                 cnt[*s.begin()]++;//当前是左端点，但是下个是右端点，cnt++
             }
             if(s.size() ==  && p[i].second <  && p[i+].second >){
                 cnt[*s.begin()]--;//如果首先插入地是一段单独区间（l r），去掉这个区间则区间数量-1
             }
         }
         int t = -;
         for(int i = ;i<=n;i++){
             t = max(t,cnt[i]);
         }
         cout<<ans+t<<endl;
     }
     return ;
 }