[LOJ#2743][DP]「JOI Open 2016」摩天大楼

• 题目传送门

• DP 经典题

• 考虑从小到大把数加入排列内

• 如下图（\(A\) 已经经过排序）：

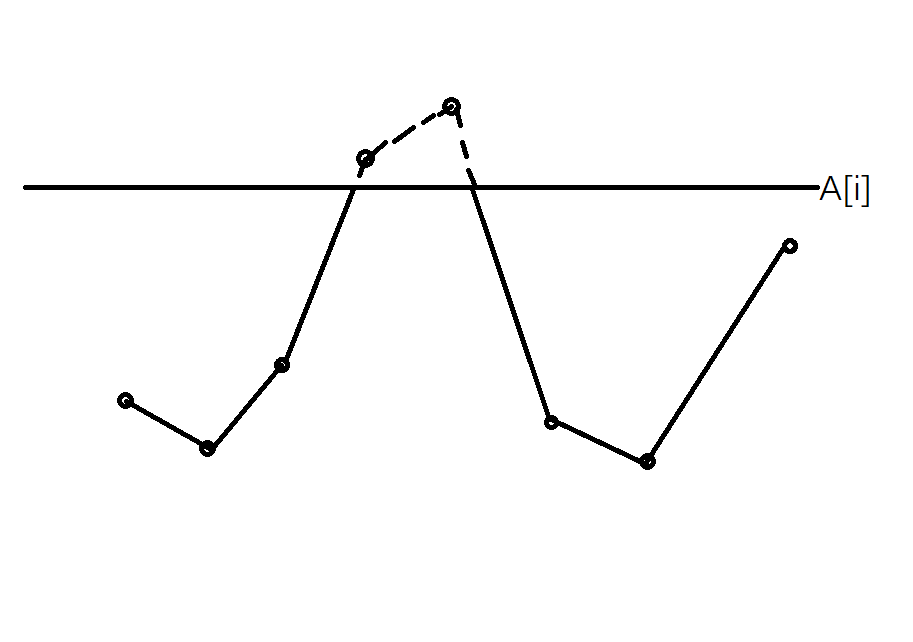
• 我们考虑如上，在 \(i\) （ \(A_i\) ）不断增大的过程中，维护上面直线 \(y=A_i\) 之下的部分的长度之和

• 于是我们定义 DP ：\(f[i][j][k][h]\) 表示插入了前 \(i\) 个数，分成 \(j\) 段，\(y=A_i\) 之下的部分长度之和为 \(k\) ，并且选出了 \(k\) （ \(0/1/2\) ）个边界（第 \(1\) 个或第 \(n\) 个）的方案数

• 注意这个 DP 中我们只需要保证每段是否在边界以及相邻两段之间有空位即可，不关心每段的实际位置

• 不难发现，从 \(f[i][j][k][h]\) 转移到 \(f[i+1]\) ，\(k\) 的增量是固定的，即对于每个段的两端，将直线从 \(y=A_i\) 移到 \(y=A_{i+1}\) 时每端都会多出 \(A_{i+1}-A_i\) 的长度（边界除外），于是 \(f[i][j][k][h]\) 转移到 \(f[i+1]\) 时 \(k\) 的增量为 \((A_{i+1}-A_i)\times(2j-h)\) ，设其为 \(w\) 。下面讨论几种情况进行转移：

• （1）新建一段，这一段可以放在边界除外的任意 \(j+1\) 个空隙内：

• \[f[i+1][j+1][w][h]+=f[i][j][k][h]\times(j+1-h)
  \]

• （2）合并两段：

• \[f[i+1][j-1][w][h]+=f[i][j][k][h]\times(j-1)
  \]

• （3）放在其中一段的其中一端，不改变段数，只让该段长加 \(1\) ：

• \[f[i+1][j][w][h]+=f[i][j][k][h]\times(2j-h)
  \]

• （4）新建一段并钦定其为边界：

• \[f[i+1][j+1][w][h+1]+=f[i][j][k][h]\times(2-h)
  \]

• （5）接在最左段（不能为边界）的左端并钦定为边界，或接在最右段（不能为边界）的最右端并钦定为边界：

• \[f[i+1][j][w][h+1]+=f[i][j][k][h]\times(2-h)
  \]

• 答案为 \(\sum_{i=0}^Lf[n][1][i][2]\) ，复杂度 \(O(n^2L)\) ，可以将第一维滚动以优化空间

Code

#include <bits/stdc++.h>
#define vf(ii, jj) f[op ^ 1][ii][w][jj]

template <class T>
inline void read(T &res)
{
	res = 0; bool bo = 0; char c;
	while (((c = getchar()) < '0' || c > '9') && c != '-');
	if (c == '-') bo = 1; else res = c - 48;
	while ((c = getchar()) >= '0' && c <= '9')
		res = (res << 3) + (res << 1) + (c - 48);
	if (bo) res = ~res + 1;
}

const int N = 105, M = 1005, rqy = 1e9 + 7;

int n, l, a[N], f[2][N][M][3], ans;

int main()
{
	read(n); read(l);
	for (int i = 1; i <= n; i++) read(a[i]);
	if (n == 1) return puts("1"), 0;
	std::sort(a + 1, a + n + 1);
	f[0][0][0][0] = 1; a[0] = a[1];
	for (int i = 0; i < n; i++)
	{
		int op = i & 1;
		for (int j = 0; j <= i + 1; j++)
			for (int k = 0; k <= l; k++)
				f[op ^ 1][j][k][0] = f[op ^ 1][j][k][1] = f[op ^ 1][j][k][2] = 0;
		for (int j = 0; j <= i; j++)
			for (int k = 0; k <= l; k++)
				for (int h = 0; h < 3; h++)
				{
					if (!f[op][j][k][h]) continue;
					int w = k + (a[i + 1] - a[i]) * (j * 2 - h), cf = f[op][j][k][h];
					if (w > l) continue;
					vf(j + 1, h) = (1ll * (j + 1 - h) * cf + vf(j + 1, h)) % rqy;
					if (j) vf(j - 1, h) = (1ll * (j - 1) * cf + vf(j - 1, h)) % rqy;
					vf(j, h) = (1ll * (j * 2 - h) * cf + vf(j, h)) % rqy;
					if (h < 2)
					{
						if (j) vf(j, h + 1) = (1ll * (2 - h) * cf + vf(j, h + 1)) % rqy;
						vf(j + 1, h + 1) = (1ll * (2 - h) * cf + vf(j + 1, h + 1)) % rqy;
					}
				}
	}
	for (int i = 0; i <= l; i++) ans = (ans + f[n & 1][1][i][2]) % rqy;
	return std::cout << ans << std::endl, 0;
}