[ARC152D] Halftree题解

• 很好的一道题，即使是我这种菜鸡也感到心潮澎湃。

• 直觉有余，证明不足。思路有余，推导不足。

• 无论是什么比赛，对拍都是最有效的查错方式。

• 本篇题解里的所有图片采用 graph_editor 制作。

---

题意简述

给你一张没有边的，\(n\) 个点的图，点的编号从 \(0\) 到 \(n-1\)，再给你一个参数 \(k\)。你可以执行以下操作任意次：

• 选择点 \(u\) 和点 \(v\)，将其连边，并且将 \((u+k) \mod n\) 与 \((v+k) \mod n\) 连边。

你需要在第一行输出你的操作次数 \(m\)，在第 \(2\) 到 \(m+1\) 行输出你每次操作选择的 \(u\) 和 \(v\)，使得经过你的操作，这张图变为无重边，无自环的一棵树。

思路整理

在以下的推导中，我们设 \(to_i=(i+k) \mod n\)，\(p=gcd(n,k)\)。

你发现，如果 \(n\) 为偶数，必然无解。因为每次加入两条边，不可能产生奇数条边。

对于奇数，你想到了这样一种形式：将 \(0\) 和 \(to_0\) 连边，这时 \(to_0\) 会与 \(to_{to_0}\) 连边。之后将每个点 \(u\) 与 \(0\) 连边，此时 \(to_u\) 会与 \(to_0\) 连边。每次新加两个点，一开始有三个点。这样加下去总能满足条件。这看上去很对，你很高兴，认为今天能上大分。

显然电脑很不高兴，她给你这样一组数据：\(n=15,k=6\)。

你把图画出来，发现有一丝不对劲：

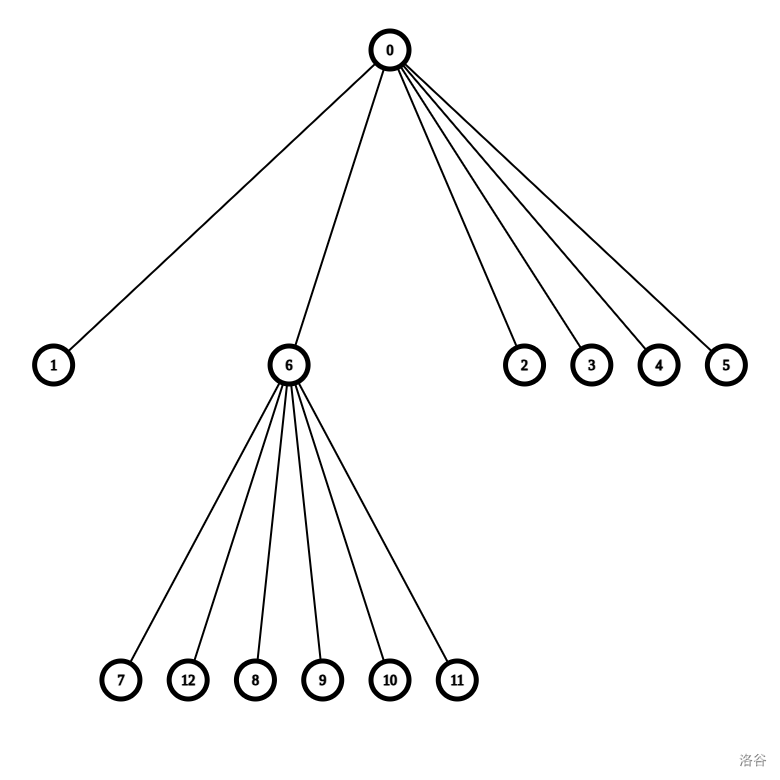
少了两个点！\(13\) 本来要和 \(7\) 对 \(0\) 和 \(1\) 连边，但 \(7\) 被 \(5\) 抢了！

你转念一想：我直接让 \(5\) 跟 \(7\) 连边，那么 \(13\) 就会与 \(7\) 连边。问题似乎被解决了！

然后你造出来了 \(p\) 条链。

你很不高兴，决定将这 \(p\) 条链连起来。

你试着将 \(0\) 和 \(1\) 连起来，发现 \(to_0\) 和 \(to_1\) 也连了起来。这就是个环了，于是你决定将 \(1\) 所在的那条链全断开。

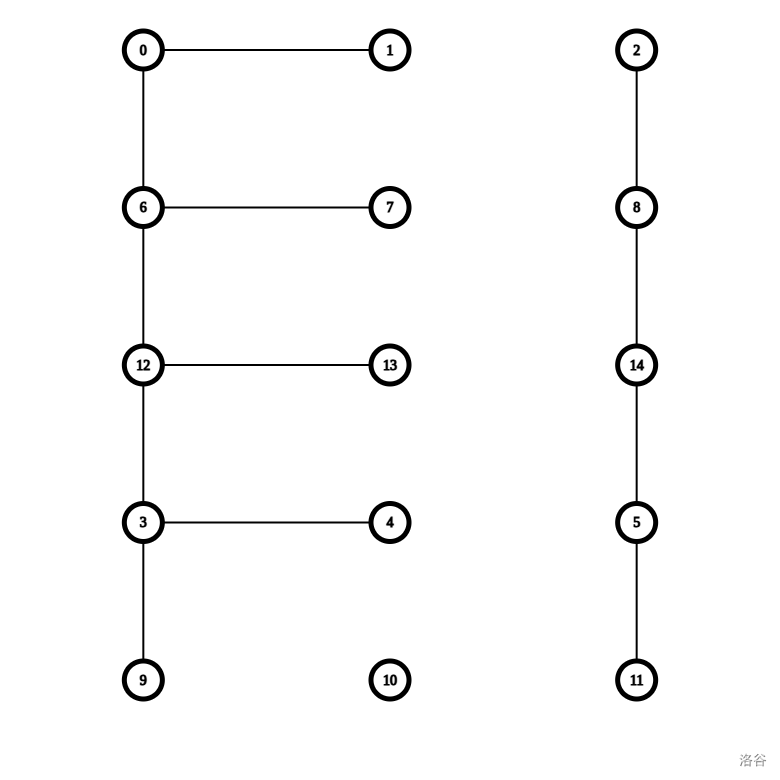
这种方案有两个问题：

1. 最后一行没人管
2. 最后一列没人管

你试图将两个没人管的东西连起来: \(10\) 和 \(11\)，然后会连上 \(1\) 和 \(2\)。。。成了！

如果有更多列呢？那就多做几遍！

这里提供一份 \(n=35,k=7\) 的答案图。

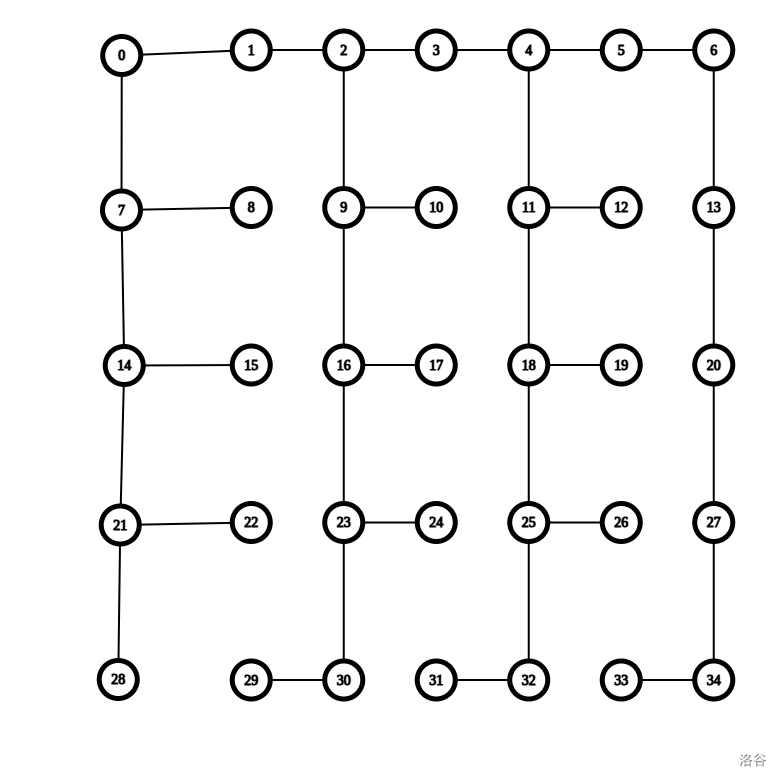
作为一个精益求精的人，你想要证明当 \(n\) 为奇数时都能构造出上面的树。

你发现，构造出这个树的条件为每条链的节点数为奇数，且有奇数条链。

显然，当 \(n\) 为奇数时 \(p\) 为奇数。第一条链的节点集合 \(S\) 为 \(0,p,2p,...,(n/p-1)*p\)。总共 \(n/p\) 个点。奇数被奇数整除得奇数

所以，第 \(i\) 条链可以表示为 \(0+(i-1),p+(i-1),...(n/p-1)+(i-1)\)。起点从 \(0\) 到 \(p-1\) 都有可能，所以总共有 \(p\) 条链。为奇数。

你很高兴，上了大分。因为这一场有许多人都被小学追及问题难住了。

代码很短，不给代码。