C#.NET实现二分查找

二分搜索法

定义

二分法查找，也称为折半法，是一种在有序数组中查找特定元素的搜索算法。

适用范围

当数据量很大并且有序时，适宜采用该方法。

基本思想

假设数据是按升序排序的，对于给定值key，从序列的中间位置k开始比较，

如果当前位置arr[k] 值等于key，则查找成功；

若key小于当前位置值arr[k]，则在数列的前半段中查找,arr[low, mid - 1]；

若key大于当前位置值arr[k]，则在数列的后半段中继续查找arr[mid + 1, high]，

直到找到为止,时间复杂度:O(log(n))

算法难点

对边界条件细节掌握，也就是区间状态。区间状态基本为下边两种。

若是区间为[left, right]既while(left<=arr.Length-)：更新状态方式left = mid + 1; right = mid - 1;

若是区间为[left, right)既while(left<arr.Length)：更新状态方式left = mid + 1; right = mid;

代码实现（模板）

该代码是实现区间为[left,right]的。

public static int BinarySearch(int[] nums, int target)
{
    // 避免当 target不存在与数组,多次进行循环运算
    if (target < nums[0] || target > nums[nums.Length - 1])
    {
        return -1;
    }
    int left = 0, right = nums.Length - 1;
    while (left <= right)
    {
        //1.此处避免数据量过大，超出int范围。2.位运算效率比较高
        int mid = left + ((right - left) >> 1);
        if (nums[mid] == target)
            return mid;
        else if (nums[mid] < target)
            left = mid + 1;
        else if (nums[mid] > target)
            right = mid - 1;
    }
    return -1;
}

题目练习

给出的题目由易到难，熟练掌握二分法，及其边界处理问题。

704. 二分查找

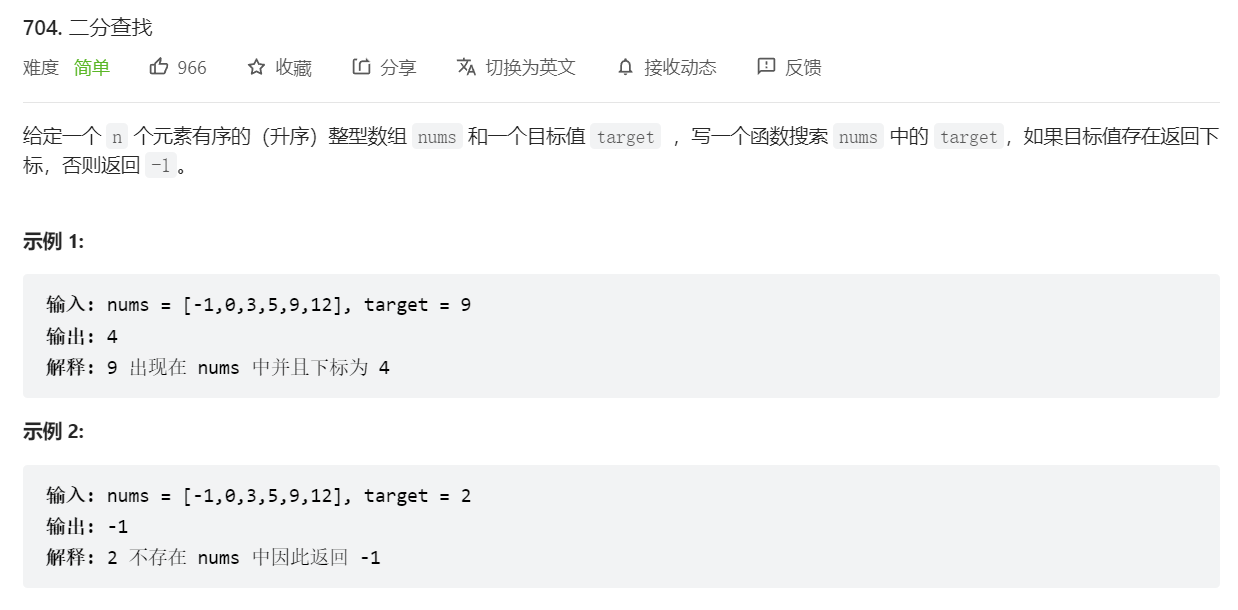
//这道题是最简单的，也是我们二分法的模板。之后关于二分法的题目，都是基于此题给的变形。
public int Search(int[] nums, int target) {
  int left = 0;
  int right = nums.Length - 1;
  int mid = 0;
  while (left <= right)
  {
      mid = left + ((right - left)>>1);
      if (nums[mid] == target)
      {
          return mid;
      }
      else if (nums[mid] < target)
      {
          left = mid + 1;
      }
      else {
          right = mid - 1;
      }
  }
  return -1;
}

153. 寻找旋转排序数组中的最小值

public int FindMin(int[] nums)
{
    int left = 0;
    int right = nums.Length - 1;
    int mid;
    while (left <= right)
    {
        mid = left + ((right - left) >> 1);
        // 注意是当中值大于等于右值时，
        if (nums[mid] >= nums[right])
        {
            left = mid + 1;
        }
        else
        {
            right = mid;
        }
    }
    return nums[right];
}

面试题 10.03. 搜索旋转数组

public int Search(int[] arr, int target)
{
  if (arr[0]==target) return 0;
  int left = 0;
  int right = arr.Length - 1;
  int mid;
  while (left <= right)
  {
      mid = left + (right - left)>>1;
      if (arr[mid] == target)
      {
          while (mid > 1 && arr[mid - 1] == arr[mid])
          {
              mid--;
          }
          return mid;
      }
      else if (arr[mid] > arr[left])//左侧递增
      {
          if (arr[left] <= target && target < arr[mid])
          {
              right = mid - 1;
          }
          else
          {
              left = mid + 1;
          }

      }
      else if (arr[mid] < arr[left])
      {
          if (arr[mid] < target && target <= arr[right])
          {
              left = mid + 1;
          }
          else
          {
              right = mid - 1;
          }

      }
      else {
          left++;
      }
  }
  return -1;
}

题库：二分查找分类练习