2021牛客暑期多校训练营3 J 思维

传送门 J-Counting Triangles_2021牛客暑期多校训练营3 (nowcoder.com)

题目

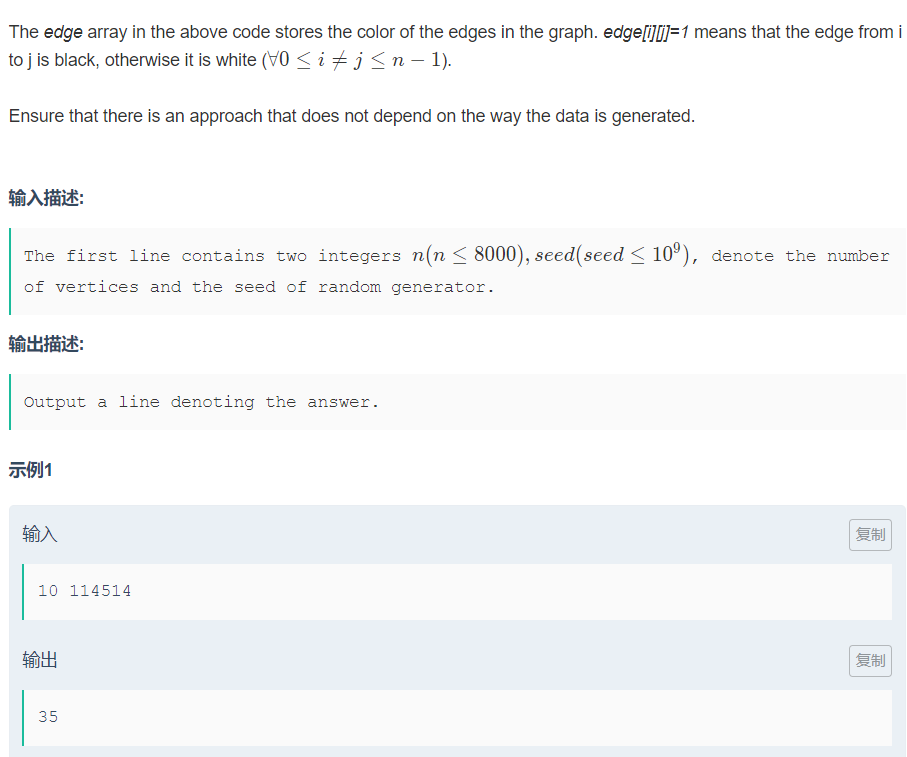
Goodeat finds an undirected complete graph with n vertices. Each edge of the graph is painted black or white. He wants you to help him find the number of triangles (a, b, c) (a < b < c), such that the edges between (a, b), (b, c), (c, a) have the same color. To avoid the input scale being too large, we use the following code to generate edges in the graph.

namespace GenHelper
{
    unsigned z1,z2,z3,z4,b,u;
    unsigned get()
    {
        b=((z1<<6)^z1)>>13;
        z1=((z1&4294967294U)<<18)^b;
        b=((z2<<2)^z2)>>27;
        z2=((z2&4294967288U)<<2)^b;
        b=((z3<<13)^z3)>>21;
        z3=((z3&4294967280U)<<7)^b;
        b=((z4<<3)^z4)>>12;
        z4=((z4&4294967168U)<<13)^b;
        return (z1^z2^z3^z4);
    }
    bool read() {
      while (!u) u = get();
      bool res = u & 1;
      u >>= 1; return res;
    }
    void srand(int x)
    {
        z1=x;
        z2=(~x)^0x233333333U;
        z3=x^0x1234598766U;
        z4=(~x)+51;
      	u = 0;
    }
}
using namespace GenHelper;
bool edge[8005][8005];
int main() {
  int n, seed;
  cin >> n >> seed;
  srand(seed);
  for (int i = 0; i < n; i++)
    	for (int j = i + 1; j < n; j++)
        	edge[j][i] = edge[i][j] = read();
 	return 0;
}

　　

题意

给出两个数, n为几个顶点, 运行题目代码后, edge数组　edge[i][j]==1的道路为黑色 ==0的道路为白, 只有同色的才能相连构成三角形, 求构成三角形的个数

题解

一. n*(n-1)*(n-2)/6是C³_n ,即n个数可以组成的全部三角形数目(无颜色差别， 1为黑 0为白)

二. 每个三角形三条边的颜色可以为 111    000   011   001 其中前二者为所求, 后二者为所弃。 若要直接求, 比较复杂,

但后二者有简单规律：必有两个顶点使得 它的两个邻边为0和1

方法:枚举1~n的点x, (连接x为1的和连接x为0)连成三角形就是后二者的情况

最后结果即为n个数可以组成的全部三角形数目 - 无法构成的三角形

代码

#include <iostream>

using namespace std;

typedef long long LL;
const int N = 2e5+10;
LL st[N];
LL res = 0;

//此为题中所给代码
namespace GenHelper
{
    unsigned z1,z2,z3,z4,b,u;
    unsigned get()
    {
        b=((z1<<6)^z1)>>13;
        z1=((z1&4294967294U)<<18)^b;
        b=((z2<<2)^z2)>>27;
        z2=((z2&4294967288U)<<2)^b;
        b=((z3<<13)^z3)>>21;
        z3=((z3&4294967280U)<<7)^b;
        b=((z4<<3)^z4)>>12;
        z4=((z4&4294967168U)<<13)^b;
        return (z1^z2^z3^z4);
    }
    bool read() {
      while (!u) u = get();
      bool res = u & 1;
      u >>= 1; return res;
    }
    void srand(int x)
    {
        z1=x;
        z2=(~x)^0x233333333U;
        z3=x^0x1234598766U;
        z4=(~x)+51;
          u = 0;
    }
}
using namespace GenHelper;
bool edge[8005][8005];
int main() {
    int n, seed;
    cin >> n >> seed;
    srand(seed);
    for (int i = 0; i < n; i++)
        for (int j = i + 1; j < n; j++)
            edge[j][i] = edge[i][j] = read();

    //从此开始为手写代码
    LL ans = 0;
    for(int i = 0; i < n; i ++)
        for(int j = 0; j < n; j ++)
            if(edge[i][j])
                st[i] ++;
    for(int i = 0; i < n; i ++)
        ans += st[i] * (n-1-st[i]);
    cout << (LL)n*(LL)(n-1)*(n-2)/6 - ans/2;
     return 0;
}